一周前终于结束了长达3个月的2025下半年系统架构设计师软考备考历程, 自己对于UE几何部分的学习节奏也断了好长一阵子. 目前比较感兴趣的且能对自己的几何功力有所提升的便是网格生成与曲面细分, 而这两部分恰好是《GPU Gems 3》 中几何一章的两小节内容. 如此一来, 仿佛一下子找到了指路明灯, 接下来一段时间也会以此作为几何部分的学习纲领. 先从网格生成部分开始, 以本文解读一篇在网格生成领域十分经典的论文《Dual Marching Cubes: Primal Contouring of Dual Grids》.
参考材料
1. Schaefer S, Warren J. Dual marching cubes: Primal contouring of dual grids[C]//12th Pacific Conference on Computer Graphics and Applications, 2004. PG 2004. Proceedings. IEEE, 2004: 70-76.
1. 特征隔离
给定一个隐函数$f(x, y, z)$和一个八叉树, 作者的目标是在特征隔离中为八叉树中的每个单元格构造一个顶点, 该顶点将成为对偶网格的顶点. 与对偶轮廓法(Dual Contouring) 等方法不同, 此顶点并非与表面的几何特征对齐, 而是与隐函数本身的特征对齐. 因此, 每个顶点不仅包含位置坐标$(x, y, z)$, 还包含一个标量值$w$, 表示该顶点处隐函数值$f(x, y, z)$的估计结果.
$\\$ 作者从隐函数中检测特征的方法与论文M. Garland and P. S. Heckbert. Surface simplification using quadric error metrics. In Proceedings of SIGGRAPH 97, Computer Graphics Proceedings, Annual Conference Series, pages 209–216, Los Angeles, California, August 1997. ACM SIGGRAPH / Addison Wesley.提出的表面特征检测技术类似. 为了确定近似单元格内隐函数特征的顶点, 作者使用二次误差函数(QEFs)(如文献M. Garland and P. S. Heckbert. Surface simplification using quadric error metrics. In Proceedings of SIGGRAPH 97, Computer Graphics Proceedings, Annual Conference Series, pages 209–216, Los Angeles, California, August 1997. ACM SIGGRAPH / Addison Wesley所述). 生成这些QEF时, 作者在单元格$c$上采样的网格点处计算关于隐函数$f(x, y, z)$图像的切平面. 在采样点$(x_i, y_i, z_i)$处, 隐函数$w = f(x, y, $$ z)$图像的切平面方程为$w = T_i(x, y, z)$, 其中$$T_i(x, y, z) = \nabla f(x_i, y_i, z_i) \cdot ((x, y, z) – (x_i, y_i, z_i)),$$$\nabla f(x_i, y_i, z_i)$是函数$f(x_i, y_i, z_i)$的梯度. 为了构建QEF, 作者对这一方程进行平方, 并对所有采样点求和, 从而得到:$\begin{align}E(w, x, y, z) = \sum_{i} \frac{(w – T_i(x, y, z))^2}{1 + \left | \nabla f(x_i, y_i, z_i) \right | } . \label{QEF} \end{align}$该表达式的分母对每个切平面的贡献进行归一化, 以使其具有相等的权重.
$\\$ 接下来, 作者在单元格$c$内最小化该二次函数以找到对偶网格$(w, x, y, z $$ )$的顶点. 若最小化求解器存在欠定性(即解不唯一), 作者采用P. Lindstrom. Out-of-core simplification of large polygonal models. In Proceedings of SIGGRAPH 2000, Computer Graphics Proceedings, Annual Conference Series, pages 259–262. ACM Press / ACM SIGGRAPH / Addison Wesley Longman, July 2000.的方法,通过伪逆矩阵将最小值点定位到尽可能靠近单元格$c$中心的位置.
$\\$ 需要注意的是, 作者对特征隔离阶段的描述并未限定隐函数$f(x, y, z)$的具体输入格式. 其描述允许多种可能的输入形式. 例如, Marching Cubes中常用的均匀标量网格可被采用, 其中将网格中的每个立方体视为三线性函数, 从而使得$f(x, $$ y, z)$和其梯度$\nabla f(x, y, z)$在单元内有明确定义. 此外, 也可以将上述采样限制在均匀网格的顶点上, 并通过差分法在这些顶点处估计$\nabla f(x, y, z)$. 后者的优势在于能够在网格顶点处定义单一的法线$\nabla f(x, y, z)$, 而非前者产生的多个不连续法线. 有向距离场则提供了另一种替代方案, 其通过非均匀标量场可提供更精确的梯度信息, 从而更准确地重构尖锐特征.
$\\$ CSG树(Constructive Solid Geometry Trees) 是本算法的另一种潜在输入形式. CSG通过集合操作(如并集, 交集) 组合几何体, 其中CSG树的叶节点表示基本几何体(如平面, 圆柱体等), 内部节点则表示集合操作. 在作者的算法中使用此类CSG树时, 必须将其转换为具有明确定义梯度$\nabla f(x $$ , y, z)$的标量值函数$f(x, y, z)$. 对于CSG树的叶节点, 作者将其几何体替换为对应的基本体带符号欧几里得距离函数(如平面、圆柱体等). 对于内部节点, 则将并集和交集操作分别替换为最小值和最大值操作. 计算CSG树在某点$(x, y, z)$处的值时, 只需计算该点对所有叶节点的距离函数, 并在CSG树的内部节点上执行对应的Min/Max操作. 计算梯度$\nabla $$ f(x, y, z)$时, 需在CSG树的每个叶节点处评估对应的梯度, 并在Min/Max操作中随函数值一同向上传递. 图1与图2均通过计算CSG树生成.
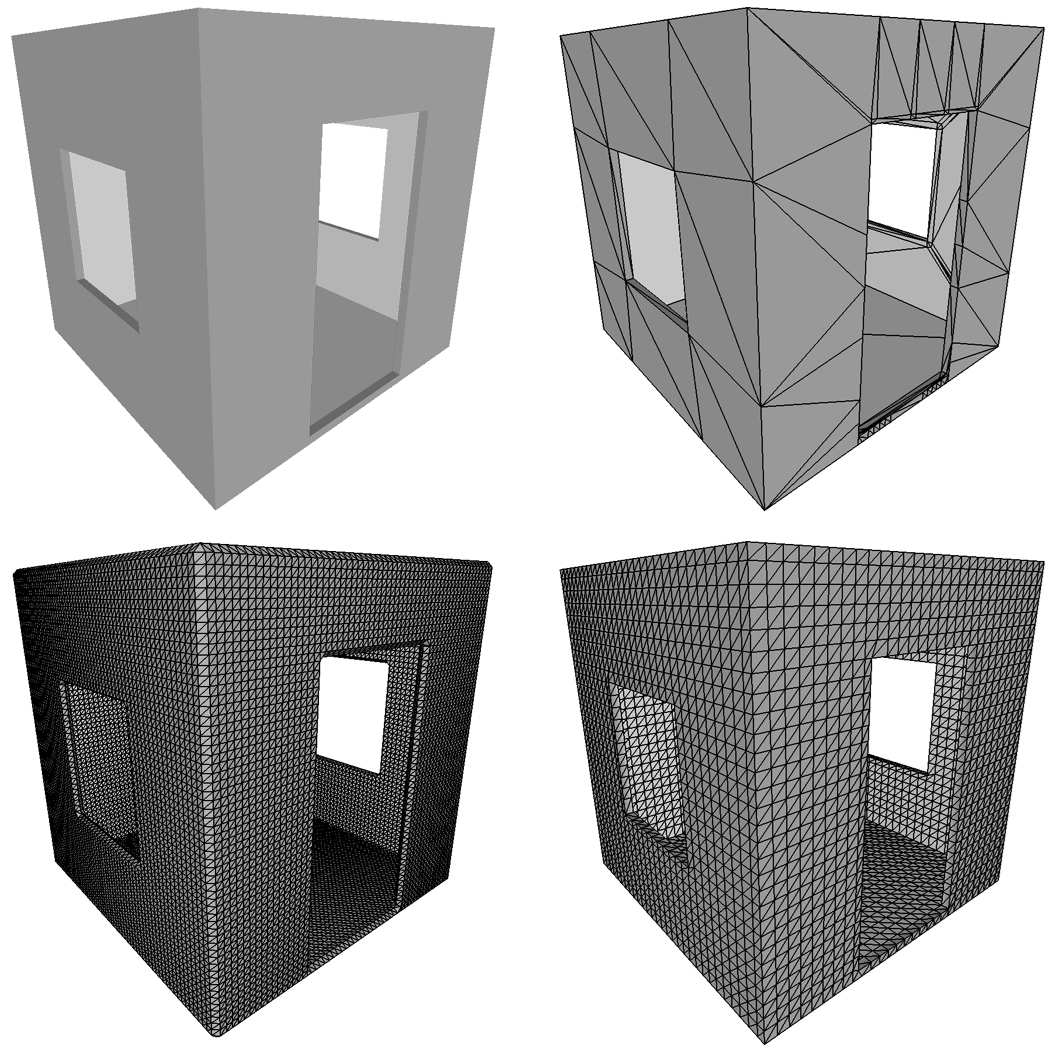
$\cdot$ Marching Cubes(左下, 67,000面)
$\cdot$ 对偶轮廓法(右下, 17,000面)
$\cdot$ 对偶Marching Cubes(右上, 440面)
使用对偶Marching Cubes时, 等值面网格的规模对墙壁厚度不敏感.

$\cdot$ 对偶Marching Cubes(右上)
$\cdot$ Marching Cubes(左下)
$\cdot$ 对偶轮廓法(右下)
1.1 八叉树构建
作者当前对特征隔离的描述假设已存在一个八叉树, 用于将空间划分为单元格. 然而, 有时需要对隐函数$f(x, y, z)$进行近似, 使其误差在给定的容差范围$\epsilon$内. 为了实现这一目标, 作者提出了一种自顶向下的八叉树构建算法.
$\\$ 该八叉树构建算法从一个初始单元格$c$开始构建八叉树. 作者使用上述采样算法在均匀网格上对隐函数$f(x, y, z)$进行精细采样(也可采用随机采样策略). 接下来, 利用这些采样点构建QEF并对其进行最小化. 若公式$\eqref{QEF}$计算的误差大于给定容差$\epsilon$, 则将该单元格划分为8个子单元格, 并递归执行此过程. 当八叉树的所有叶节点误差均小于容差$\epsilon$时, 算法终止, 最终构建出最小化的八叉树以近似隐函数$f(x, y, z)$.
2. 拓扑创建
给定一个八叉树, 特征隔离会生成对偶网格的顶点(表面将从这些顶点中提取). 拓扑创建则实际生成对偶网格的拓扑结构. 该对偶网格在拓扑上与八叉树互为对偶. 因此, 对于八叉树中的每个顶点, 会在对偶网格中生成一个单元格, 其顶点是包含该八叉树顶点的所有立方体内的特征顶点. 图3展示了从一个示例四叉树生成的对偶网格拓扑(其中对偶网格的每个顶点位于其对应立方体的中心). 尽管作者的算法操作于八叉树, 但本节讨论将简化为四叉树以方便说明; 然而, 此处描述的算法可自然扩展到八叉树.
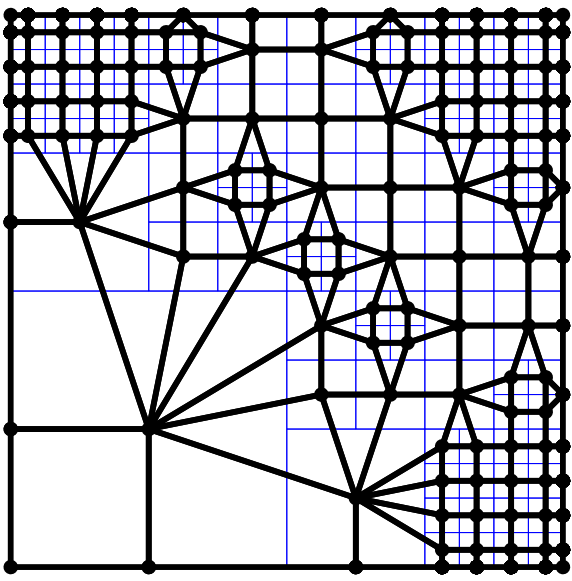
给定一个四叉树$q$, 任务是以高效的方式枚举对偶网格的每个单元格, 而无需在四叉树中显式查找邻居节点. 作者的解决方案是一种递归遍历算法, 通过枚举所有共享同一顶点的叶方块元组来实现对偶网格单元格的生成. 该方法是对文献T. Ju, F. Losasso, S. Schaefer, and J. Warren. Dual contouring of hermite data. ACM Transactions on Graphics, 21(3):339–346, July 2002. ISSN 0730-0301 (Proceedings of ACM SIGGRAPH 2002).中四叉树遍历策略的简单扩展.
$\\$ 该遍历过程涉及三个递归函数: faceProc[$q_1$], edgeProc[$q_1$, $q_2$]和vertProc[$q_1$, $q_2$, $q_3$, $q_4$].
$\\$ $\cdot$ 给定四叉树中的一个内部节点$q_1$, faceProc[$q_1$]函数会递归调用其四个子节点, 并对$q_1$的所有四对边相邻子节点调用edgeProc, 以及对$q_1$的四个子节点调用一次vertProc.
$\\$ $\cdot$ 给定一对边相邻的内部节点$q_1$和$q_2$, edgeProc[$q_1$, $q_2$]函数会递归调用跨越$q_1$和$q_2$共同边的两对边相邻子节点, 并对$q_1$和$q_2$中接触该共同边中点的四个子节点调用一次vertProc.
$\\$ $\cdot$ 给定四个共享同一顶点的内部节点$q_1$, $q_2$, $q_3$和$q_4$, vertProc[$q_1$, $q_2$, $q_3$, $q_4$]函数会递归调用这四个子节点(它们在该共享顶点处交汇).
$\\$ 在这些递归调用中, 若某个节点$q_i$是叶节点, 则其子节点不可用于后续递归调用. 此时, 对于递归所需的每个$q_i$的子节点, 均传递一个$q_i$的副本作为参数. 图4展示了这三个函数的相互递归结构.
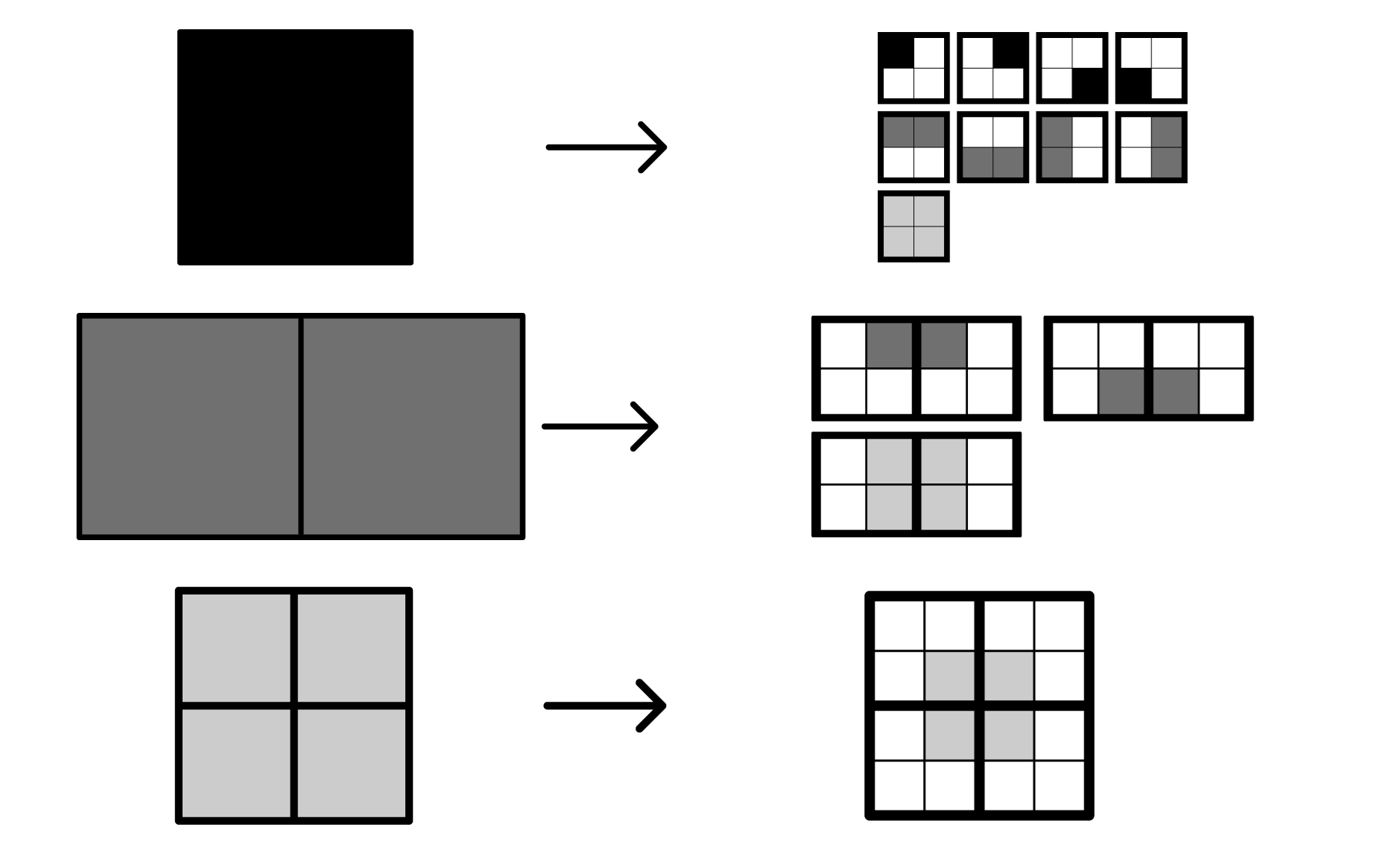
当所有节点$q_i$均为四叉树叶节点时, 这些函数的递归调用终止. 在vertProc的终止条件中, 可得到四个共享同一角点的叶节点. 此时, 通过连接特征隔离阶段中为每个叶节点生成的顶点, 拓扑上形成一个正方形, 从而构建一个对偶网格单元格. 在自适应情况下, 其中一个叶节点$q_i$可能被重复使用, 导致几何上形成三角形. 需注意, 该方法的运行时间与四叉树的规模呈线性关系, 因为四叉树中的每个方块对应一次faceProc调用, 每条边对应一次edgeProc调用, 每个顶点对应一次vertProc调用.
$\\$ 如上所述,调用faceProc[$q_1$]仅生成位于四叉树根节点内部的单元格. 为了将对偶网格扩展到四叉树的边界, 作者将四叉树视为一个$3 \times 3$退化矩形网格中的中心方块. 在此网格中, 四个方块退化为四叉树的边, 而剩余四个方块退化为四叉树的顶点. 通过将四叉树的根节点与其每个退化边相邻的邻居节点作为参数调用edgeProc, 即可生成与四叉树对应边接触的单元格. 同样地, 通过将根节点的每个顶点与其三个退化顶点邻居节点作为参数调用vertProc, 即可生成与该顶点接触的单一对偶单元格. 图4展示了使用此方法生成的对偶网格, 其中包含位于网格边和角点的顶点.
3. 对偶网格等值面提取
在生成对偶网格后, 作者通过将Marching Cubes算法简单扩展至这些对偶网格来提取表面. Marching Cubes最初仅设计用于处理轴对齐的立方体, 而论文所使用的对偶网格单元格在空间中具有任意位置的顶点. 作者的解决方案是: 注意到由上述递归算法生成的对偶网格中每个单元格在拓扑结构上等价于一个立方体(尽管由于八叉树的多分辨率结构, 某些顶点可能重复). 利用对偶网格顶点处的标量值, 作者计算所有包含符号变化的边上的交点. 随后, 通过Marching Cubes提供的查找表生成该单元格内部表面的拓扑结构.
$\\$ 由于对偶网格的顶点位于隐函数$f(x, y, z)$的特征上, 该对偶网格的等值面同样表现出尖锐特征, 类似于扩展Marching Cubes和对偶轮廓化方法生成的结果. 对偶Marching Cubes相较于这些方法的主要优势在于: 生成等效等值面所依赖的底层八叉树更加稀疏.
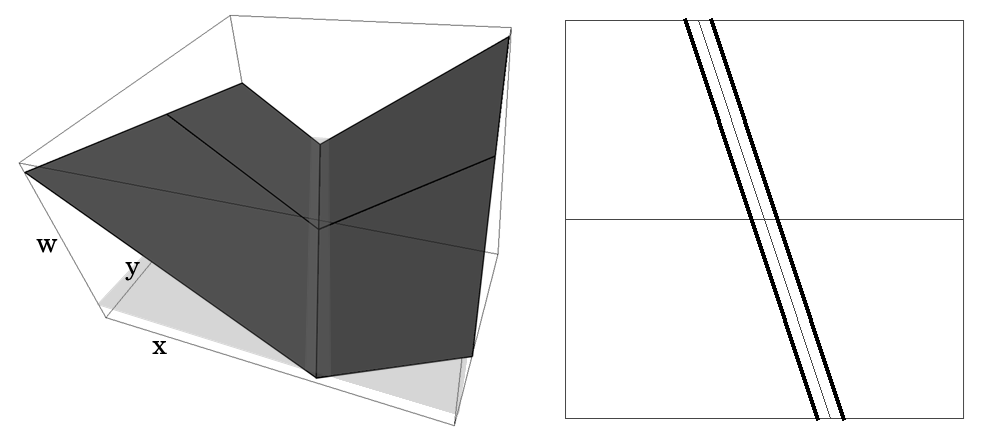
$\\$ 为了理解这一现象, 考虑一个二维示例. 图5(左) 展示了两条紧密排列的平行线(如图5右侧所示) 的距离函数. 这两条线性函数通过取每条线距离函数的最大值得到(最大值运算用于构造交集区域: $max(d_1, d_2) \le 0$时, 表示同时在两条线的内侧区域, 即两条线的交集). 图左侧显示了$f(x, y)$的对偶网格的结构, 由四个四边形单元格组成, 其中顶点的高度记为标量值$w$. 对每个四边形进行等值线提取, 会生成四条线段, 且结果与两条平行线的间距无关.
$\\$ 在EMC(扩展Marching Cubes) 和对偶轮廓化等方法中, 用于解析该函数两条独立等值线的原始网格密度依赖于两条等值线的分离距离(依赖原始网格的分辨率分离两条紧密平行线. 若两条线间距小于网格分辨率, 原始网格会将它们合并为一条轮廓线; 它们需要高分辨率网格即更多细分层级才能解析紧密特征, 导致计算开销剧增). 在图5示例中, 两条线的交集区域形成一个尖锐的V形凹角, 传统方法难以用低分辨率网格解析该凹角.
$\\$ 而在对偶Marching Cubes中, 用于等值线提取的网格会自适应距离函数的特征(如梯度方向), 而非等值线本身的特征. 这一区别通常避免了因等值线紧密排列而需要高分辨率细分的需求. 通过特征隔离阶段, 顶点位置由QEF优化确定, 强制顶点对齐距离函数的梯度方向, 能精确对齐两条线的交点(如图5中四边形顶点位于两条线的交线上), 无需高分辨率细分. 在图5示例中, 对偶Marching Cubes通过对偶网格的自适应性直接捕捉凹角特征. 即使两条线间距极小, 对偶网格仍能生成独立的线段(如图5左的四条线段), 而传统方法需细分网格才能达到相同效果.
作为一个更复杂的三维示例, 考虑图1中的薄壁房间. 该房间通过一系列基于平面基元的CSG操作设计而成. 左下角的网格是传统Marching Cubes在细网格上对距离函数的等值面提取结果, 用于还原薄壁结构(注意尖锐边缘的圆化现象). 右下角的网格由对偶轮廓化生成, 能精确还原房间形状, 但因墙壁过薄, 无法简化网格中大量的平坦区域. 作者通过计算八叉树, 以近似原始CSG树结构. 右上角的表面由对偶Marching Cubes通过对该八叉树的对偶网格进行等值面提取生成. 该表面不仅精确还原了房间形状, 且使用了显著更少的多边形. 值得注意的是, 当房间墙壁厚度减小时, 传统Marching Cubes和对偶轮廓化所需的多边形数量会急剧增加, 而对偶Marching Cubes生成的多边形数量基本保持恒定.
$\\$ 使用Marching Cubes对这些对偶网格进行等值面提取的一个缺点是, 当对偶网格的顶点可能因QEF优化误差或八叉树细分不充分而接近平面$w $$ = 0$时, 生成的三角形容易因顶点分布不均而变得极扁平, 从而生成大量细长三角形(Sliver Polygons). 解决该问题的方法是尽可能将对偶网格的顶点精确调整到平面$w = $$ 0$上. 这一调整对最终等值面的效果是消除大部分细长三角形. 具体实现中, 作者首先计算受限QEF $E(0, x, y, z)$的最小化解$\hat{p}$. 若该解$\hat{p}$对应的残差(即$E(\hat{p})$的绝对值) 小于阈值$\epsilon$, 则使用该解作为对应立方体的顶点; 否则, 按之前方法执行特征隔离. 图6展示了对偶Marching Cubes生成的等值面, 其中细长三角形已被消除.
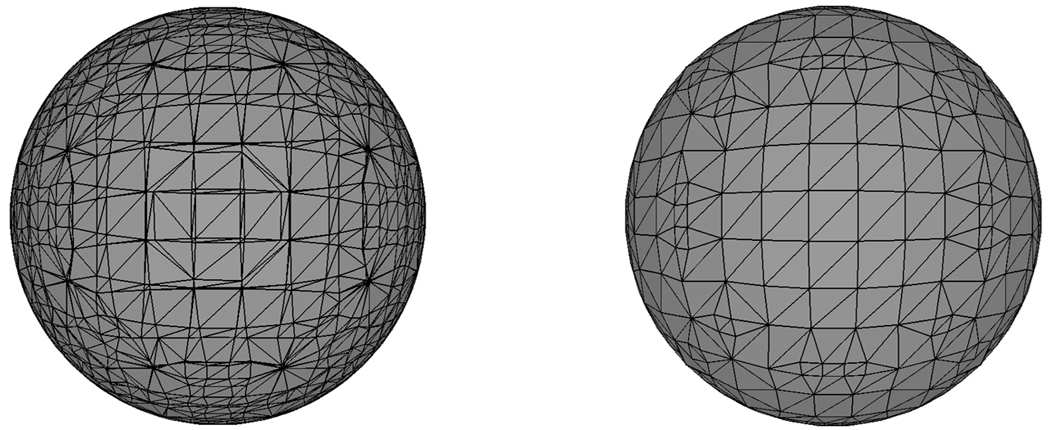
图2展示了一个通过CSG操作序列构建的火箭模型示例, 以及使用对偶Marching Cubes, Marching Cubes和对偶轮廓化生成的近似模型. 该火箭是一个典型的测试案例, 因为其底部薄鳍具有五角形旋转对称. 当几何特征与坐标轴对齐时, 原始网格(如Marching Cubes) 表现良好, 但这些薄鳍与原始网格的参数线方向不一致. 因此, Marching Cubes和对偶轮廓化等方法难以准确还原这些薄壁特征. 相比之下, 对偶Marching Cubes通过构建与薄鳍对齐的对偶网格, 即使薄鳍未与八叉树对齐, 也能精确重建这些细节.
$\\$ 图7展示了使用马和龙模型进行自适应表面提取的效果. 在马的模型中, 身体部分的多边形比颈部和腿部更粗糙; 尽管腿部相对于身体其他部分较细, 但仍能被准确还原. 龙的模型同样展示了自适应多边形化, 其面部和足部的多边形比身体其他部分更精细. 尽管作者仅在这些模型上直接运行Marching Cubes算法, 未添加任何多分辨率扩展, 但对偶网格的结构自然生成了这些多分辨率等值线. 此外, 由于作者使用Marching Cubes对这些模型进行等值面提取, 生成的表面在拓扑上是流形.

4. 实现
在实现该方法时, 作者将算法可能接受的各种输入抽象为一个函数, 该函数可被求值以确定采样点处的标量值和梯度. 由于作者使用QEFs估计尖锐特征, 体素化方法中会遇到与表面建模方法相同的问题. 例如, 在最小化公式$\eqref{QEF}$时, 特征顶点可能位于生成它的立方体之外. 此时,作者如论文P. Lindstrom and C. T. Silva. A memory insensitive technique for large model simplification. In Proceedings of the conference on Visualization ’01, pages 121–126. IEEE Computer Society, 2001.所述, 在立方体边界上对QEF进行最小化.
$\\$ 此外, 需要注意的是, 并没有强制要求必须将顶点放置在距离函数的特征上. 虽然这种放置方式能够还原尖锐特征, 但也可以修改特征隔离阶段, 直接在每个立方体的中心采样$f(x, y, z)$. 这样生成的算法与论文R. N. Perry and S. F. Frisken. Kizamu: A system for sculpting digital characters. In Proceedings of SIGGRAPH 2001, Computer Graphics Proceedings, Annual Conference Series, pages 47–56. ACM Press / ACM SIGGRAPH, August 2001.中的等值面提取算法类似, 但避免了自适应配置中产生的特殊情况, 且始终生成拓扑流形表面.
$\\$ 就性能而言, 对偶网格的等值面提取耗时不高于原始网格. 由于对偶网格更贴合隐函数$f(x, y, z)$的几何特征, 因此可使用更稀疏的网格提取表面, 从而实际减少等值面提取时间. 然而, 对偶网格的生成仍存在一定耗时. 在3GHz频率的Pentium处理器上, 基于上述八叉树构建算法, 特征隔离阶段关于图1所示的输入耗时0.1秒, 关于图2所示的输入中耗时2.5秒, 而关于图7所示的输入则耗时数分钟.
$\\$ 解决这一问题的一种方法是认识到对偶网格的大部分单元并不直接参与生成提取的表面. 只有包含符号变化的对偶网格单元才会包含表面片段. 因此, 可以开发一种算法, 将特征隔离和拓扑生成阶段限制在包含表面片段的单元内. 作者预计该优化方法的速度将与其它流行方法相当.
5. 未来工作
作者认为, 对偶网格生成的概念不仅适用于等值面提取领域. 实际上, 该网格生成过程本质上是在立方体域上对给定函数$f(x, y, z)$进行分段线性逼近. 基于这一特性, 对偶网格生成应成为一种优秀的自适应拼接方法, 用于处理多个相交的参数曲面—— 因其能将对偶网格的边自适应于交线. 在机器人领域, 距离函数在路径规划等应用中也起着关键作用. 因此, 该对偶网格的另一潜在应用是: 计算距离函数的精确自适应逼近, 并在对偶网格上执行路径规划.