最近两天下班时间都在晚上十二点以后了, 实在有点吃不消, 大概这就是游戏行业的常态叭…… 上午请了个假休息一下, 重新学习了一下射影平面及齐次坐标, 有了更深的理解, 特此记录一下~
$\\$ 直观上来理解, 射影平面其实是欧几里得空间上直线与平面的高度抽象, 因为射影平面不能无自交地嵌入三维欧几里得空间, 因此在三维欧几里得空间中, 我们并不能完美地表现射影平面, 也就是很难去想象它究竟长啥样. 这里的“完美” 是指既不能把直线“掰弯”, 也不能引入“无穷远点” 等不直观的概念, 但三维空间下的射影平面(空间) 可以嵌入到四维欧几里得空间, 这与克莱因瓶类似.
参考材料
1. 射影平面的直观理解
2. 计算机视觉笔记1:白话射影几何
3. 写给大家看的“透视除法” —— 齐次坐标和投影
4. GAMES101-现代计算机图形学入门-闫令琪 P4
1. 射影空间
从等价类的角度来看, 若两个点均处于过原点的同一直线上, 则在射影空间中是等价的, 均表示同一个点; 若两个平面平行, 则在射影空间中也是等价的, 均表示同一条直线. 射影空间的一个重要性质是任何两条直线相交于一点(因为引入了无穷远点).
$\\$ 为了直观理解, 通常会使用球面来可视化射影空间, 如考虑球心位于原点的单位球, 则所有过原点的直线均和这一球面有且有2个交点, 剔除对径点后便可以得到射影空间一一对应的投影点. 这样我们便可以利用该投影点在球面上的法向去定义该点的齐次坐标. 这在理论上也是有保证的, 因为射影空间同胚于球面粘合对径点.
$\\$ 因为直线的定义是最短路径(的延申), 而在球面上最短路径是以圆弧的形式呈现的, 因此射影空间中的直线在球面投影是一段圆弧. 实际上, 任意一段圆弧是半球面和平面 $Ax + By + Cz = 0$的交集. 我们可以利用该平面的法向$(A, B, C)$来定义直线的齐次坐标. 特别地, 当$A = B = C = 0$时定义的直线是一条无穷远的直线.
2. 齐次坐标
射影空间中的坐标被称为齐次坐标, 利用齐次坐标, 我们可以将点进行分类, 当把射影空间嵌入到四维空间中以后, 每个点的齐次坐标都可以用一个四维向量$(x, $$ y, z, w)$来表示, 当射影空间中两个点的$w$分量相同时, 则意味着它们在射影空间的同一个平面上. 在数学上, 没有所谓的“不正确” 的齐次坐标, 使用齐次坐标时让$w=1$仅仅是用于计算机图形学中的投影变换.
$\\$ 接下来再浅谈一下图形学中的齐次坐标, 这主要用于顶点Shader上的投影变换. 当将一个点$(x,y,z,1)$进行投影变换以后其$w$分量一般会变化, 如在近平面$z = $$ n$上的点经投影变换以后其$w$分量会变为$n$. 在顶点Shader执行完毕以后会进行透视变换, 即将每一个点的齐次坐标$(x, y, z, w)$的每一个分量都除以$w$($w$一般不为0), 此时点的齐次坐标变为$(x/w, y/w, z/w, 1)$, 而这依旧在射影空间中表示同一个点, 或许这也是图形学上进行透视变换的理论依据叭, 能模拟人眼看到的世界. 最后只取$(x/w, y/w, z/w, 1)$的前两个分量构成一个二维向量, 即转化为屏幕上的一个点(虽然后面还需要进行视口变换, 因此还会有一定的拉伸).
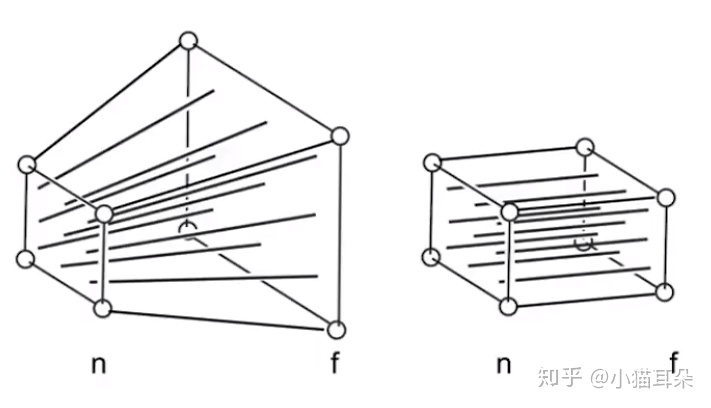
PS: 现代渲染流水线进行透视投影的算法是先把远平面进行压缩, 把视锥体压缩成一个长方体, 然后再通过正交投影矩阵变换到中心位于原点的边长为2的立方体$[-1, 1] \times [-1, 1] \times [-1, 1]$中, 如下图所示. 目前我还不大明白这个算法为何要将透视投影转化为正交投影的原因(直接利用把在近平面上的截影不香么……), 有待后续研究.