这周迎来了久违的周末, 能在家宅两天真的是幸福哈哈! 这周准备结束了齐次空间部分的学习~ 在传统的渲染管线中, 齐次空间的裁剪是发生在顶点Shader以后, 透视除法之前的, 目的就是剔除视锥体以外的物体, 减少不必要的渲染.
参考材料
1. 计算机图形学补充2:齐次空间裁剪(Homogeneous Space Clipping)
2. 齐次空间的裁剪
3. 一篇文章彻底弄懂齐次裁剪
图片基本来自于知乎文章与CSDN博客
1. 三角网格与视锥体的裁剪
显然, 在进行三角面的裁剪时需要判断点和裁剪平面的关系, 如下图所示:
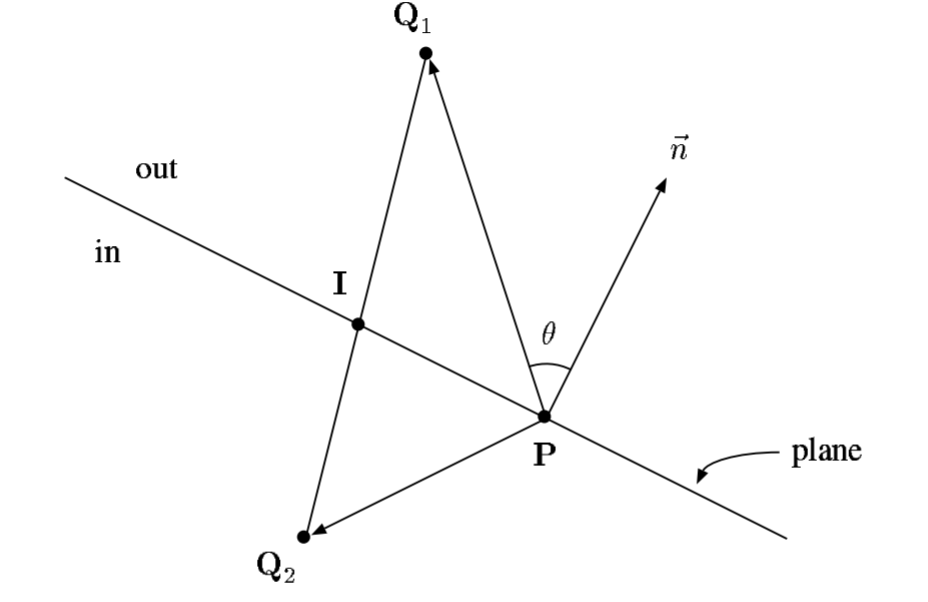
其中, $Q_1, Q_2$为三角面上的两个顶点, $P$是裁剪平面上的点, $\overrightarrow{n}$为裁剪平面上的法向, 不妨令$$d_1 = (Q_1-P) \cdot \overrightarrow{n}, \\ d_2 = (Q_2-P) \cdot \overrightarrow{n}.$$显然, 当$d_1$与$d_2$异号时表示边$Q_1 Q_2$与裁剪平面相交, 不妨设其相交点为$I$. 则$$I = Q_1 + t(Q_2 – Q_1),$$其中, $t = |Q_1 I| / |Q_1 Q_2|$, 这可以由相似三角形性质可得: 在$I$点处作一条裁剪平面上的垂线, 则可得拥有一对对顶角的相似三角形.
$\\$ 这样一来, 对于任一三角网格而言, 都可以进行逐边遍历, 把每一条边经过裁剪平面裁剪得到的部分保留下来, 即可得到最终的经裁剪后的网格. 更进一步地, 当考虑三角网格与视锥体的裁剪时, 只需要考虑逐个裁剪平面的裁剪即可(共6个裁剪平面). 而由这个思路诞生的算法也是鼎鼎大名的Sutherland-Hodgeman裁剪算法.
2. 齐次(射影) 空间下的裁剪
传统的渲染管线中, 经过Vertex Shader与透视除法以后, 便会将顶点变换到NDC中, 原来的视锥体也会变成标准立方体$[-1, 1] \times [-1 $$ , 1] \times [-1, 1]$, 此时6个裁剪平面为$$x = 1, x = -1, y = 1, \\ y = -1, z = 1, z = -1.$$但需要清楚的是, 渲染管线并不是在NDC中进行裁剪的, 具体原因会在下文阐述. 实际上, 渲染管线是在齐次空间中进行裁剪的. 那么问题就转化为需要找到NDC中的6个裁剪平面在齐次空间中对应的裁剪平面. 根据透视除法性质, 易知齐次空间中的6个裁剪平面为$$w = x, w = -x, w = y, \\ w = -y, w = z, w = -z.$$接下来以$w = x$裁剪平面为例, 讨论一下三角形边与$w=x$裁剪平面的裁剪计算. 假设三角形边$Q_1 Q_2$与$w = x$裁剪平面交点为$I$, 插值系数为$t$, 则$I = Q_1 + $$ t(Q_2 – Q_1),$ 如下图所示:
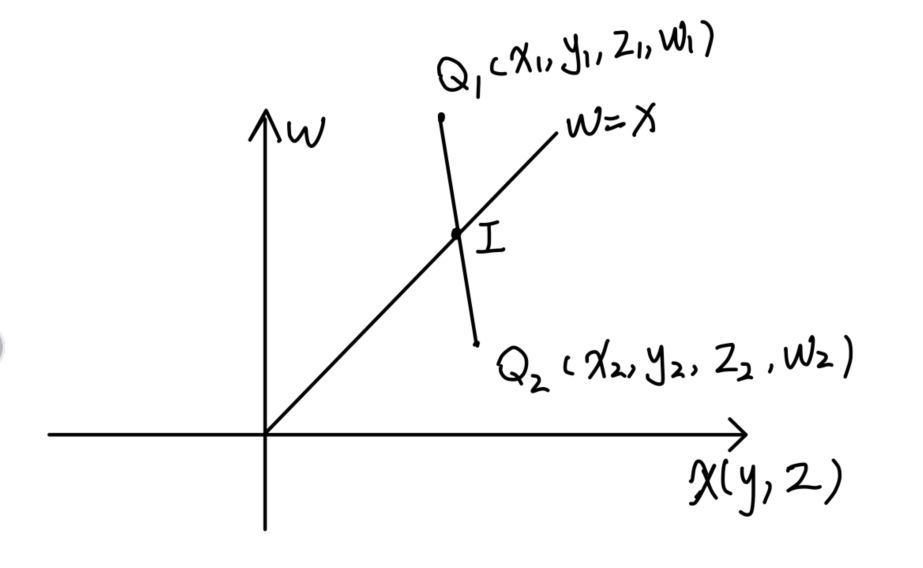
又交点$I$落在裁剪平面$w = x$上, 因此交点$I$的$x$分量与$w$分量相等, 即$$x_1 + t(x_2 – x_1) = w_1 + t(w_2 – w_1),$$解得$t = (x_1 – w_1) / ((w_2 – w_1) – (x_2 – x_1)).$ 类似可得其它裁剪平面的交点计算结果.
PS: 除了考虑上述6个裁剪平面之外, 通常还会增加一个关于$w = $$ 10^{-5}$裁剪平面的裁剪, 防止在进行透视除法时出现除0错误.
3. 裁剪后的顶点组合
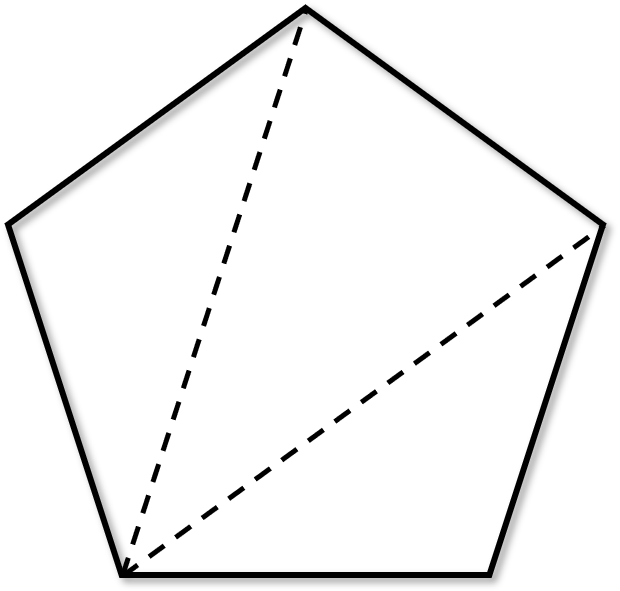
上述裁剪过程后, 一般得到的只是裁剪后的顶点, 已经丢失了三角形的信息. 因此需要将顶点重新组合成若干个三角形, 其中的组合顺序是十分重要的, 一般与原三角形的顶点顺序保持一致(顺时针方向或逆时针方向), 这也是为了防止在进行正面剔除或者背面剔除的时候出现奇怪的结果. 如下图所示是一种非常简单的组合三角形的方法, 这也是我之前在进行点云重采样研究计算局部最佳估计网格时采用的网格化方法, 但我并不确定现代图形API组合三角形的算法, 其效果有待进一步验证.
4. 裁剪的重要性
除了减少渲染消耗以外, 裁剪还有一个重要意义: 防止出现奇怪的渲染结果. 在观察空间中, 若一个点的坐标是$(x,y,z,1)$, 通过投影变换以后得到其齐次坐标$(x’ $$ , y’, z’, -z)$, 再经透视除法得到$(x”, y”, $$ z”, w”) = (x’/-z, y’/-z, z’ / $$ -z, 1)$. 显然, 如果当一个点在观察点后面, 其观察坐标的$z$分量大于0(假设观察点位于观察空间原点, 且遵循右手原则, 即$z$轴朝向屏幕外), 那么经投影变换以后以后得到的齐次坐标的$w$分量将小于0, 从而经透视除法以后$(x”, y”, z”, $$ w”)$的$x, y, z$分量都均变号, 导致部分三角网格发生上下左右翻转的现象, 如下图所示.
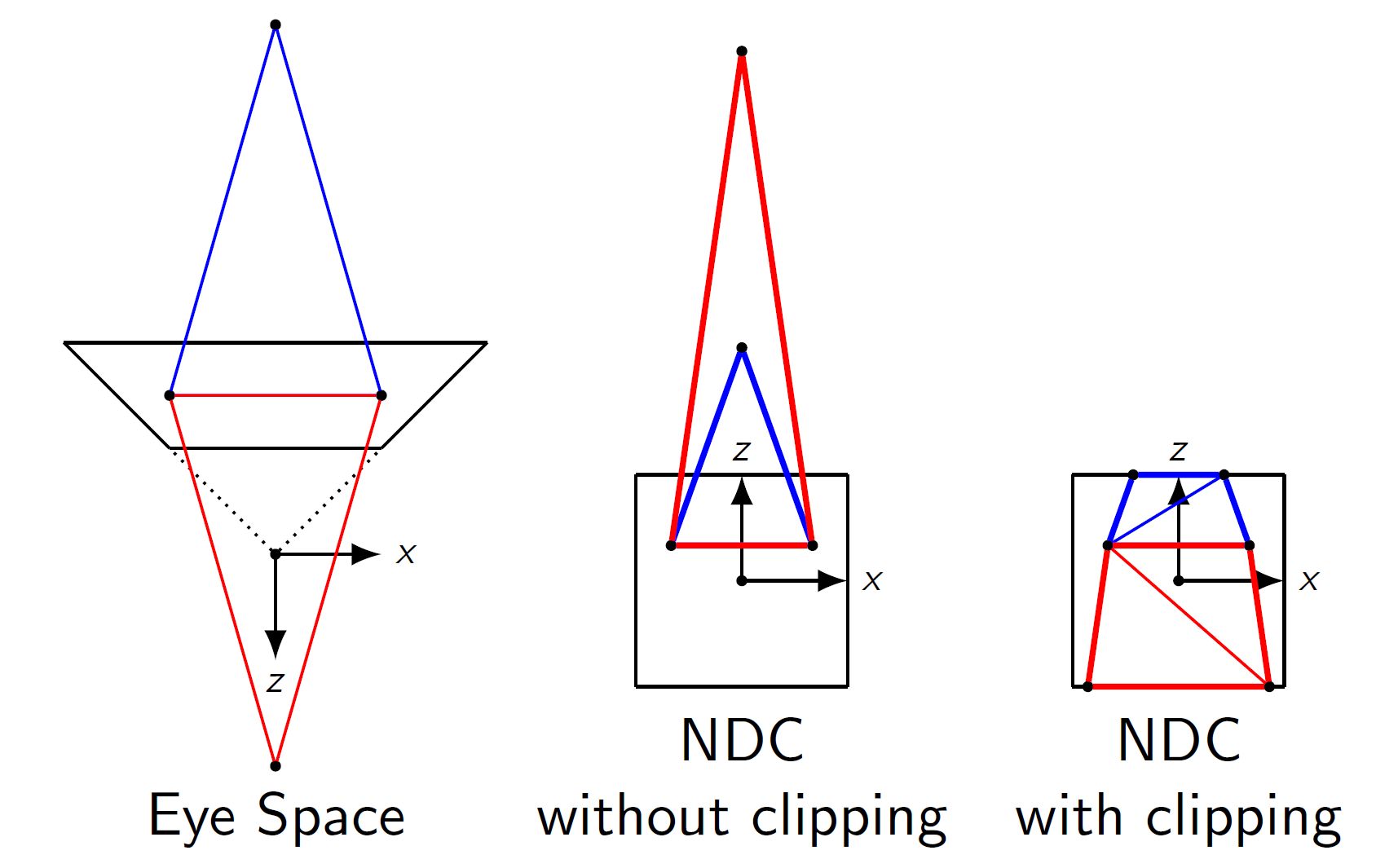
5. 为什么不在投影除法后进行裁剪
先看看一般的投影矩阵定义:
$$\begin{bmatrix}
cot(\theta/2)/r & 0 & 0 & 0\\
0 & cot(\theta/2) & 0 & 0\\
0 & 0 & (N + F) / (N – F) & -2NF/(N – F)\\
0 & 0 & -1 & 0\\
\end{bmatrix},$$其中, $\theta$是相机的FOV, $z = N$表示近平面, $z = F$表示远平面, $r$是近平面$z = N$的长宽比.
$\\$ 对于观察空间中的点$(x, y, z, 1)$, 经投影矩阵的作用后得到点的齐次坐标$(x’, y’ $$ , z’, -z)$, 其中$x’ = cot(\theta/2) / r \cdot x$, 显然$x’$与$x$呈线性关系, 同理可得$y’$与$y$, $z’$与$z$均呈线性关系. 但在经透视除法以后, 得到坐标$(x”, y”, z”, w”)$, 此时$x” $$ = cot(\theta/2) \cdot x / (r \cdot -z)$是关于$x$与$z$的函数, 与$x$不再呈线性关系, 同理可得$y”$与$y$, $z”$与$z$均不再呈线性关系. 若在透视除法以后进行剔除, 则无法再使用线性插值, 否则点的颜色, 纹理等属性在经线性插值以后都将产生异常.
6. 为什么能在齐次空间中进行裁剪
由于投影矩阵表示的是一系列仿射变换, 而仿射变换是并不改变点的颜色, 纹理等属性的, 故在齐次空间下裁剪后再采用线性插值也是不会产生顶点属性的异常的. 但这里就有一个问题: 在齐次空间中裁剪后得到的点, 经过透视除法以后在NDC中有没有可能被剔除呢? 答案是不会的.
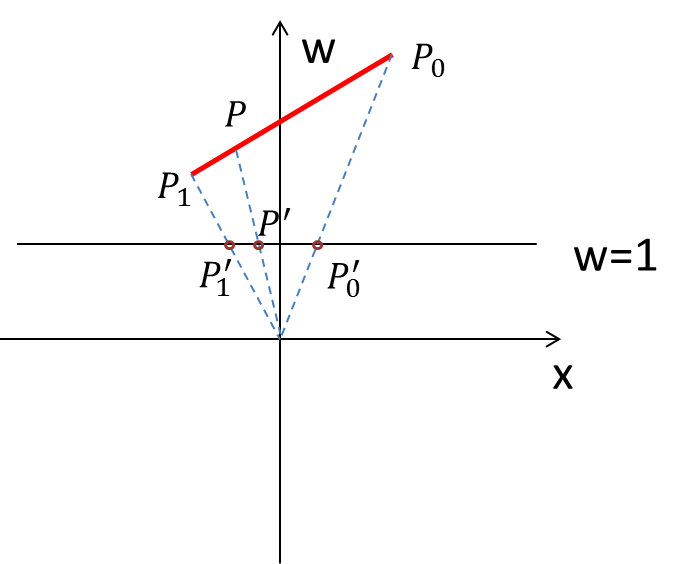
$\\$ 为了方便展示, 不妨将$y, z$分量固定, 下图展示了分量$w$与分量$x$的关系, 图中同时包含了齐次空间与NDC中的点, 图中没有画出来的是辅助线$w = x, w = -x$. 所谓的透视除法就是将齐次空间中的一点与原点相连后得到的直线与$w = 1$求交, 从而齐次空间中的点与经透视除法后落在$w = 1$上的点是一一对应的. 显然, 图中的$P_0,P_1$均位于$-x \le w \le x$区域内, 说明是在齐次空间中经裁剪后得到的点, 那么在经过透视除法以后得到的点的$x$分量必定也落在$[-1, 1]$内; 更进一步地, 经$P_0, P_1$线性插值得到的点$P$, 必定是位于视锥体内的(视锥体是一个凸多面体), 在经过透视除法以后得到的点$P’$的$x$分量必定也落在$[-1, 1]$内, 说明也是在标准立方体$[-1, 1] \times [-1, 1] \times $$ [-1, 1]$内的.