这周周末刮台风, 所以只能”被迫”呆在家里2333 这周主要针对粘合映射的部分作了一些学习的补充, 之前在看书的时候对书上一些粘合的例子并不理解, 所以便在B站上找了个拓扑系列的视频进行学习, 确实有了进一步的理解, 本文便是记录一下粘合映射相关的内容. (PS: 不得不说, 拓扑系列的中文视频教程实在是太少了, 在此再次感谢浙理工的庄晓波老师的辛勤创作~~~)
参考材料
1. 基础拓扑学
粘合映射相关的内容其实还是蛮多的, 具体细节可以参考庄晓波老师的视频(P20-P23), 我觉得细节讲解得十分到位~ 接下来只记录几个需要注意的点.
1. 商映射可以既不是开映射也不是闭映射
考虑一下商映射的定义: 设$X,Y$为两个拓扑空间, $f:X \to Y$是一个将$X$映射到$Y$的满射, 若$V$是$Y$中的开集当且仅当$f^{-1}(V)$是$X$中的开集, 则称$f$是一个将$X$映射到$Y$的商映射. 显然, $f(f^{-1}(V)) = $$ V$是成立的, 因为$f$是一个满射. 但由于在$X$中并非所有开集都可以写成$f^{-1}(V), V \subset Y$的形式, 故商映射并不一定是一个开映射或者闭映射.
2. 商空间中的子集开当且仅当其关于粘合映射的原像开. 换言之, 粘合映射是商映射.
3. 粘合映射的复合映射还是一个粘合映射, 粘合映射的顺序在同胚意义上不影响最终的粘合结果.
这个命题的直观证明可以参考庄晓波老师的基础拓扑学频道的P22教程(老师在视频起始处便讨论这个问题).
4. 进行粘合映射时对径点是根据粘合方向变动的.
如下图展示了两种不同方向的对径点, $A$与$A’$, $B$与$B’$分别表示两对对径点, 对径点会被粘合映射映射到同一点上.
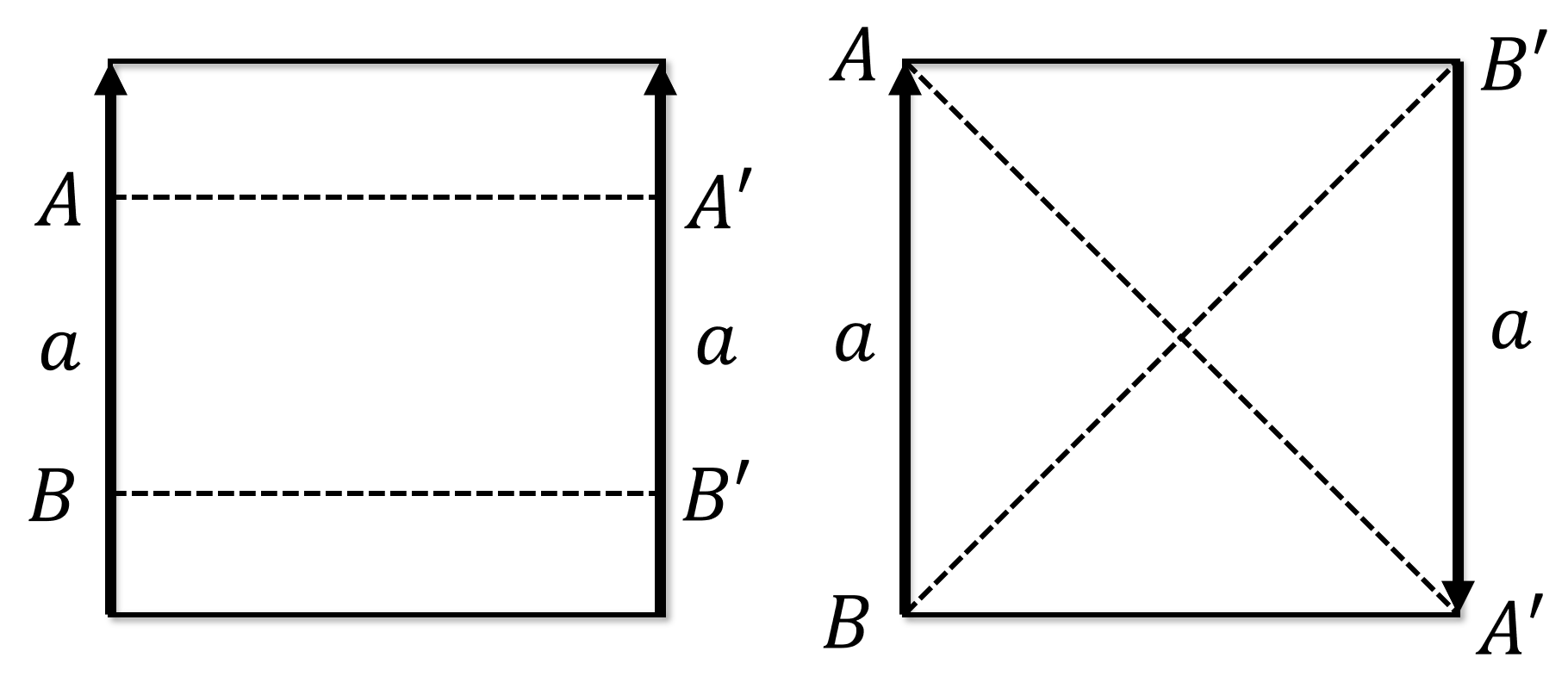
总的来说, 粘合映射是一个非常有意思的映射, 里面的例子都值得学习一波~ 下图列出了一些常见的粘合方式及粘合后所得的空间:
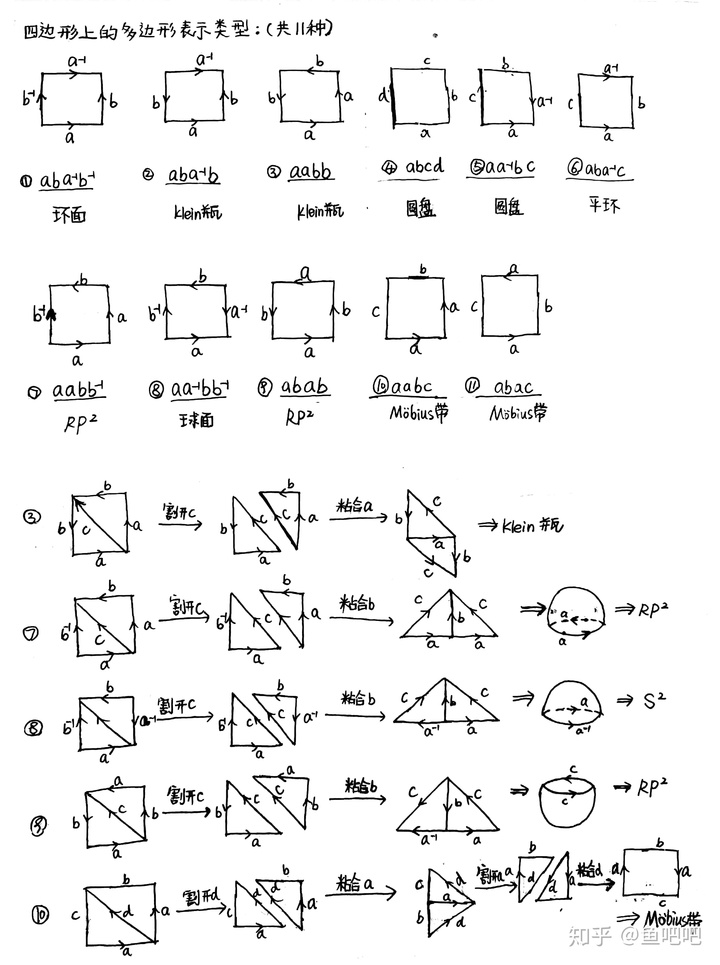
(图片来源: 闭曲面的分类及曲面的三角剖分)