本文主要用于记录学习傅孝明老师的数字几何处理课程时对自己有所启发的笔记~
视频链接: 数字几何处理-中国科学技术大学-傅孝明
Contents
P1主要介绍了一些数字几何处理相关的预备知识, 如网格, 网格拓扑等的概念, 半边数据结构及常见的网格文件格式, 其实自己本来也清楚这些东西, 所以P1干货不多, 故此处不再赘述.
P2: Discrete differential geometry
非常重要的一节基础课.
2.1 Local Averaging Region
定义了网格上一个点的邻域, 主要分为三种: Barycentric Cell, Voronoi Cell以及Mixed Voronoi Cell. 其中, Voronoi Cell不一定都处在该点的1-Ring区域里. 非常重要的一个概念, 后续很多概念都会定义在Local Averaging Region上.
2.2 Normal
定义了顶点的Normal, 并不是一个Well-Defined的概念, 但定义在面上的Normal是Well-Defined的.
2.3 Gradient
定义在三角形上的梯度是通过顶点上的梯度插值得到的(重心坐标), 对于同一个三角形面片而言, 梯度是一个常值函数. 详细推导可参考: 2_Differential_Geometry
2.4 Laplace Operator
本质上是对顶点的梯度再求一次梯度, 对于同一个三角形面片而言, Laplace算子作用后得到的结果始终为0. Laplace算子主要分为Uniform Laplace算子(对应的矩阵一般是对称正定的) 和Cot Laplace算子.
2.5 Curvature
主要分为平均曲率与高斯曲率. 其中, 平均曲率是两个主曲率的平均值, 可用Laplace算子计算得到; 而高斯曲率则是两个主曲率的乘积, 可通过1-Ring区域里的角度计算得到.
P3: Mesh Smoothing(1)
之前其实学过好几次傅里叶变换了, 但感觉总是学了就忘, 归根结底是理解得不够透彻. 学了这节以后, 感觉犹如醍醐灌顶, 对傅里叶变换的理解又加深了许多~ 以1维的傅里叶变换为例: $$F(\omega)=\int_{-\infty}^{+\infty} f(x)e^{-2 \pi i \omega x}dx, \quad (1)\\f(x)=\int_{-\infty}^{+\infty} F(\omega)e^{2 \pi i \omega x}d\omega. \quad (2)$$上述两式定义了函数$f(x)$在空间域与频域之间的转换关系.
当把一个函数$f(x)$放到频域中进行讨论时, 本质上就是把$f(x)$用另外一组基函数表示, 比较特别的就是, 这里的基函数形如$$g(x)=e_\omega(x):=e^{2 \pi i \omega x}=cos(2 \pi \omega x) + isin(2 \pi \omega x),\omega \in R.$$因此, 从内积的角度来看, (1)式求得的结果就是函数$f(x)$在一个基函数$g(x)$上的投影长度. (<$f,g$>$=\int_{-\infty}^{+\infty}f(x)\overline{g(x)}dx$, 注意, 此处需要对$g(x)$做一次共轭运算.)
这样一来, (2)式即为函数$f(x)$用一组基函数$\{g(x)\}_\omega$表示的结果. 此外, 从(2)式的角度来看, 低通滤波与高通滤波本质上只是改变了(2)式的积分上下限罢了.
P4: Mesh Smoothing(2)
Mesh Smoothing(又称Mesh Denoising) 的算法主要分为三类: Filter-Based算法, 本质上就是一类迭代算法, 一般采用Gauss–Seidel迭代或者Jacobi迭代, Laplace Filtering算法是一种常见的Filter-Based算法, 被滤波作用的信号不一定是顶点位置, 也可以先把滤波作用到Normal上, 然后再通过经滤波作用后的Normal重新移动网格顶点; Optimization-Based算法, 根据问题背景提出能量函数, 可以采用交替优化的优化算法(ADMM) 来求解能量函数的极小值; Data-Driven-Based算法, 比如我们可以拟合一个函数, 通过这个函数我们可以提取出一个网格的法向(Ground-Truth), 然后再根据法向重新移动网格顶点达到去噪的目的.
P5: Mesh Parameterizations
又称Flattening或者Unfolding, 本质上就是一个映射, 主要分为Flip-Free, Locally Bijective和Bijective三种, 其条件的严格程度是从前往后层层递进的. 其中, Flip-Free的参数化算法仅要求得到的三角网格没有翻转的三角形; Locally Bijective的参数化算法不仅仅要求没有翻转的三角形, 还要求对于原始网格的边界点而言, 其1-Ring区域映射到2D平面上以后无相交的边界边; Bijective的参数化算法则要求最为严格, 直观上可以理解为Bijective = Flip-Free + Locally Bijective, 要求原始网格上的每个点都和参数化后得到的网格上的每一个点存在双射. 参数化是一个非常基础的图形学工具, 应用非常广泛, 如Texture Mapping, Normal Map, Remeshing, suface mapping, Mesh Generation等.
P5还介绍了三类常用的参数化算法, 分别是Tutte’s Barycentric Mapping, Least Squares Conformal Maps(LSCM, ASAP) 以及Angel-Based Flattening(ABF).
$\cdot$ Tutte’s Barycentric Mapping能够从理论上保证参数化结果是Bijective的, 算法的主要思路是先把边界点映射到一个凸多边形的边界上, 然后内部点是其邻居点的凸组合, 这样便可以通过求解一个线性系统来实现Bijective的参数化, 然而实际上由于数值精度的影响, 算法结果容易出现退化的三角形.
$\cdot$ LSCM定义了一个能量函数, 该能量函数描述了当前网格每个三角面片上的Jacobi矩阵(2$\times$2)与目标Jacobi矩阵的距离, 能量函数的极小值可以通过求解法方程得到, 为了避免平凡解, 通常需要固定至少两个点, 而这两个点的选取对参数化结果具有一定的影响, 这是我不大看好LSCM的原因之一.
$\cdot$ ABF则是从角度出发, 使得参数化结果的每个三角面片的角度都满足一定的条件, 最后再根据得到的角度重新移动网格顶点, 该算法也容易受到数值精度的影响, 导致在算法迭代后期会出现三角面片不上的情况, 因此为了解决这个问题, 后面也有学者在ABF基础之上通过优化能量函数的手段规避三角面片拼接不上的问题.
P6: Mesh Parameterizations与Mesh Deformation
6.1 Mesh Parameterizations
Mesh Parameterizations主要分为三类, 分别是Isometric Mapping(旋转+平移), Conformal Mapping(相似性+平移), Area-Perserving Mapping(保面积+平移), 其中, Conformal+Area-Perserving Mapping$\Leftrightarrow$Isometric.
在对原始网格的每个三角面片建立局部坐标系以后, 我们可以从Jacobi矩阵$J_t$及其奇异值$\sigma_1, \sigma_2$的角度来区分上述三种Mesh Deformation的方式.
$\cdot$ Isometric Mapping, $J_t$是一个旋转矩阵, $\sigma_1=\sigma_2=1$.
$\cdot$ Conformal Mapping, $J_t$是一个相似矩阵, $\sigma_1=\sigma_2$.
$\cdot$ Area-Preserving Mapping, $detJ_t=1$, $\sigma_1 \sigma_2=1$.
这样一来, 参数化便可以采用LSCM的思路去做, 可以构造出下述能量函数:$$E(u,L)=\sum_{t}A_t||J_t-L_t||^2_F,$$其中$L_t$为目标Transform矩阵, 当要求Isometric Mapping时, $L_t$为一个旋转矩阵; 而当要求Conformal Mapping时, $L_t$则为一个相似矩阵.
6.2 Mesh Deformation
通常会在Mesh Deformation的过程当中把一个网格分为三个区域, 分别是Fixed区域(固定不动的区域), Handled区域(用户直接操作的区域) 与Free区域(受Handled区域影响), 它们的区别主要是内部顶点的位移量.
P7: Mesh Deformation
7.1 Transformation Propagation与Multi-Scale Deformation
网格变形一般不改变顶点之间的连接关系, 仅改变顶点的位置. 目前主要有两类变形算法: Transformation Propagation与Multi-Scale Deformation. 其中, Multi-Scale Deformation是把一个网格通过Encode的操作分解成低频部分(Base Mesh) 与高频部分(Detail), 然后在对低频部分变形以后, 把高频部分加回来, 从而达到一个保细节的效果.
7.2 Differential Coordinates
相比较Transformation Propagation与Multi-Scale Deformation而言, Differential Coordinates更侧重于对顶点的梯度或者Laplace算子进行变形.
7.3 Deformation Transfer
即把一个网格的变形操作迁移到另外一个网格上, 本质上是把变形操作Encode成一系列的仿射变换, 需要先找出这两个网格的一一对应关系.
7.4 As-Rigid-As-Possible Surface Deformation
本质上定义了一个能量函数, 该能量函数衡量了变形前后网格边长的变化量. 在该框架下, 若变形前后同一条边仅相差一个旋转变换, 则认为该边的变化量极小. 该能量函数含有两个变量, 分别是顶点位置与旋转矩阵, 因此一般采用交替优化的方法.
P8: Freedom Deformation与Generalized Barycentric Coordinates
8.1 Freedom Deformation(Space Deformation)
即对整个空间进行变形, 从而间接对内含模型进行变形, 其实和样条的思想很接近.
8.2 Generalized Barycentric Coordinates
任意函数$\phi_i:P \to R, i=1,\cdots,n$被称为广义重心坐标, 若$\forall x \in P,$$\phi_i(x) \ge 0, i=1,\cdots,n$, 且$$\sum_{i=1}^{n} \phi_i(x)=1,\sum_{i=1}^{n} \phi_i(x)v_i=x.$$广义重心坐标还具备很多性质, 如拉格朗日性等.
P9: Mean Value Coordinates与Mesh Deformation
9.1 Mean Value Coordinates(MVC)
提出MVC的目的是为了逼近一个满足狄利克雷边界条件$u|_{\partial \Omega}=u_0$的调和函数$u$($u_{xx}+u_{yy}=0$, 即经Laplace算子作用后为0, $Lu=0$.), 通常是利用定义在$\Omega$的三角剖分$T$上的分片线性函数进行逼近, 其理论基础是平均值定理(Mean Value Theorem):$$u(v_0)=\frac{1}{2\pi r} \int_{\Gamma}u(v)ds.$$根据平均值定理, 我们可以得到调和函数$u$在$\Omega$的三角剖分$T$上的逼近函数$u_T$的表达式$$u_T(v_0)=\sum_{i=1}^n\phi_iu_T(v_i)$$其中$\phi_i$是与角度$\alpha_i$相关的基函数. 这样一来, 我们便可以求出逼近函数$u_T$在网格上每个顶点的值, 从而得到调和函数$u$的数值逼近表达式(非解析表达式). 需要注意的是, 满足平均值定理的函数不一定是调和函数.
9.2 Mesh Deformation
主要讲了三种Deformation的方式, 分别是Handed-Based Deformation, Cage-Based Deformation(思想类似样条) 与Skeleton-Based Deformation(感觉主要应用于骨骼动画). 这三种方式都具有局部编辑的特点, 即局部的编辑并不会影响到全局的每个点.
P10: Repairing
这节课介绍的Mesh Repairing问题更多的是一个工程问题, 所以本节课基本没有介绍算法, 主要介绍了网格的各种常见Artifact, 包括Isolated Vertices and Dangling Edges(孤立点和悬挂边), Singular Edges(或称为Complex Edges, nonmanifold Edges), Singular Vertices, Topological Noise, Orientation(面的朝向), Surface Holes, Gaps, Degenerate Elements(退化的三角形), Self-Interactions(或Overlap), Sharp Feature Chamfering(Feature丢失) 与Data Noise等. 这些存在问题的网格来源主要有两个, 分别是CAD领域或者FEM(Finite Element Method, 有限元方法) 使用NURPS(非均匀有理B样条) 设计曲面与使用3D扫描仪扫描3D实体.
其中, 我最感兴趣的一个Artifact是Topological Noise. 它主要是指网格的亏格数量异常, 相比较Ground-Truth增加了许多小的Handle或者Tunnel. 这样一种Artifact会影响到一些需要拓扑理论保证的算法结果, 如球面参数化算法的输出, 该算法一般要求输入的网格能够与球面$S^2$同胚(亏格为0).
P11: Mesh Repairing与Mappings
这节课说实话, 个人感觉没什么干货, 老师还是不断地在强调Mesh Repairing的重要性, 虽然是个偏工程的部分, 但私以为这种讲课方式还是太啰嗦了点.
11.1 Mesh Repairing
本节重点介绍了输入网格的类型.
$\cdot$ Registered Range Scans, 即Patch的集合, 这些Patch均处于同一个坐标系下, 且均表示一个扫描物体的曲面$S$的一部分, 它们之间可能存在Overlaps;
$\cdot$ Fused Range Scans, 是指一种带边界的流形网格, 通常含有Gaps, Holes或者Islands, 个人的理解是Fused Range Scans是在Registered Range Scans的基础之上融合了相互重叠的部分得到的;
$\cdot$ Triangle Soups, 即一种三角网格, 但这种三角网格的三角形之间仅存在较弱的连接关系;
$\cdot$ Triangulated NURBS Patches, 即连通的三角网格的Patch的集合, 这些Patch的边界之间可能存在Gaps或者较小的Overlaps;
$\cdot$ Contoured Meshes, 即通常由Marching Cubes, Dual Contouring或者其它多边形网格提取算法在一个体素数据集上, 如SDF结果, 提取得到的一个三角网格, 但这种网格通常包含一些Topological Artifacts, 如多余的Handles;
$\cdot$ Badly Meshed Manifolds, 即含有退化三角形的网格, 包括面积为0的三角形, 含有Caps的三角形(其中一个内角接近$\pi$), 含有Needles的三角形(其中一条边长接近0) 与翻转的三角形(其法向与相邻面的法向夹角接近$\pi$).
接下来简要介绍了几种Mesh Repairing的算法.
$\cdot$ Surface-Oriented Algorithms, 这种算法直接对输入数据进行操作, 但只对网格进行局部的修补, 因此仅适用于仅含有一些局部Artifact的Mesh Repairing, 如Gaps, Holes或者Intersections;
$\cdot$ Consistent Normal Orientation, 这种算法仅针对网格的朝向问题进行修复, 一个常见的实现思路便是从一个三角形开始处理, 判断其法向与相邻面的法向夹角是否接近$\pi$, 若接近$\pi$则反转其法向, 一路传播下去, 但我不清楚这种算法最后是否能够收敛?
$\cdot$ Surface-Based Hold Filling, 尽可能地采用光滑的Patch填补洞;
$\cdot$ Conversion to Manifolds, 目标是去除Singular Edges或者Singular Vertices, 最常见的思路便是沿着Complex Edges切开, 感觉非常地简单粗暴;
$\cdot$ Gap Closing, 直接补上Gap不难, 难点主要是补上Gap以后可能会使得网格发生畸变;
$\cdot$ Topology Simplification, 目标是对Handles进行填补, 最常见的思路是检测到Handle以后沿着Handle切开, 从而转化为两个分离网格的Hole Filling问题;
$\cdot$ Volumetric Algorithms, 目标是得到输入网格的体素表达, 如Regular Cartesian Grids, Adaptive Octrees, KD-Trees, BSP-Trees与Delaunay Triangulations. 而得到的体素表达通常已经去除了原网格的许多Artifact, 包括Intersections, Holes, Gaps, Overlaps, Inconsistent Normal Orientations, Singular Edges与Singular Vertices. 但体素表达也会带来许多问题, 包括Handles, 破坏输入网格的连接关系以及内存问题.
$\cdot$ Volumetric Repair on Adaptive Grids, 算法主要分为三步: 1. 创建网格的自适应八叉树表达. 2. 执行形态学操作. 3. 从自适应八叉树表达中提取出网格.
11.2 Mappings
主要是开了个头, 主要内容应该还是放在P12中介绍. 从数学本质上来看, 图形学的算法基本都是在寻找满足要求的Mapping(无论是网格参数化还是网格变形), 图形学中通常分为两类, 分别是Mesh-Based Mapping与Meshless Mapping(与网格无关的Mapping). 其中, Mesh-Based Mapping通常是以仿射变换的形式出现:$$f_t(x)=J_tx+b_t.$$而Meshless Mapping则通常以基函数的形式出现:$$f(x)=\sum^m_{i=1}c_iB_i(x).$$
P12: Mappings
目前通常会把求解Mapping的问题转化为一个最优化问题, 其中, 能量函数是一个与网格扭曲程度相关的函数, 约束条件通常是要求所有三角形在经过映射后是无翻转的, 当然, 在特殊领域中通常会有额外的针对性的约束条件, 本节课也没有对此进行细谈. 能量函数的形式通常如下所示:$$\min_{f}\ D(f)\\s.t.\ detJ(f(x))>0, \forall x \in M,\\S(f)\le0,$$其中, $S(f)\le0$是针对特定领域的约束, $D(f)$是一个与网格扭曲程度相关的函数, $M$为一个输入网格. 求解这种最优化问题的方法主要分为三种,
$\cdot$ 由Tutte’s Barycentric Mapping可以得到一个已经满足约束条件的初始解, 但该初始解的扭曲程度通常是比较大的, 需要进行进一步迭代.
$\cdot$ 若较难得到一个已经满足约束条件的初始解(即初始解可能依旧含有一部分翻转的三角形), 有两种方式进行处理, 一种是把优化问题转化为一个凸优化问题. 即把其约束条件进行凸化, 另外一种则是采用Local-Global的方法(其相关算法通常分为Local Step与Global Step, Local Step通常是固定我们要优化的变量, 转而去优化其它辅助变量), 不断地把当前结果投影到一个扭曲程度有界的空间当中, 迭代进行, 最终得到一个没有翻转的结果(自己的硕士论文算法也采用了类似的思想). 当然, 采用Local-Global方法的算法的收敛速度一般是比较慢的, 目前也有许多算法来针对其收敛速度进行优化, 有的是在求解器上做文章, 如牛顿法, 拟牛顿法(如BFGS, L-BFGS)等; 有的则是另辟蹊径, 如个人感觉近乎万能的安德森加速算法(以前在铁译师兄的讨论班上学过, 其思想还是非常简单有效的, 主要是在线性空间上做文章)~
$\cdot$ 采用变量转化的思想, 把优化网格顶点位置的问题转化为优化每个三角形的仿射变换的问题, 算法的主要思路是一开始给每个三角形赋予满足约束条件的仿射变换, 不断迭代, 最后根据得到的最优解把网格顶点恢复出来.
P13: PolyCube
PolyCube是一种非常特殊的几何结构(二维情形下则称为PolySquare), 其表面的法向是跟坐标轴向量平行的, 仅有6个方向, 分别是+x, -x, +y, -y, +z与-z, 通常以立方体集合的形式呈现, 类似于搭积木一般, 主要是应用于六面体网格的生成或者四边形网格的生成. 紧接着本节课主要介绍了2种经典算法,
$\cdot$ Deformation-Based Method, 算法的主要思路是对各个网格面的法向进行操作, 使其尽量与坐标轴平行.
$\cdot$ Voxel-Based Methos, 先用Deformation-Based Method对输入网格进行预处理得到一个各个网格面法向与坐标轴近乎平行的粗糙网格, 然后在这个粗糙网格上构建一个初始的PolyCube, 这个初始的PolyCube的角点(Corner) 需要尽可能地少, 且与粗糙网格的拓扑结构需要尽可能地保持一致, 如没有非流形的点, 面, 亏格数量尽可能一致(此处的亏格数量可以直接利用欧拉公式进行计算, 因为是在体网格上的, 相比较在面网格上的亏格数量的计算还是方便得多). 而对于如何构建PolyCube, 本节也介绍了两种算法, 其中一种算法的主要思路是求解一个带约束的最优化问题, 把几何上的相似性(衡量构造出来的PolyCube相比较于粗糙网格的扭曲程度) 及拓扑的不变性都作为其硬约束, 把构造出来的PolyCube的角点数量作为其能量函数.
P14: Surface Mapping
Surface Mapping旨在寻找两个网格之间的一一映射, 本节主要介绍了寻找Compatible Meshes(即顶点数量与连接关系均相同的网格集合) 之间的一一映射的算法, 其应用主要是Morphing与Attribute Transfer(包括位置, 纹理等属性的迁移) 等. 相关的算法主要有两类, 且得到的映射不一定是Bijective的, 一般是Locally Injective的.
$\cdot$ Common Base Domain算法, 把输入网格分别映射到两个中间区域, 然后再寻找这两个中间区域之间的映射, 最后把已经得到的所有映射进行复合运算即可得到输入网格之间的映射. 算法的缺点主要是Common Base Domain的构造是比较复杂的, 同时算法结果得到的映射的扭曲程度可能比较高.
$\cdot$ Parameterization-Based Method, 个人感觉本质上还是Common Base Domain算法, 不同之处在于Parameterization-Based Method的初始步骤中得到的Common Base Domain仅有一个, 此处的Common Base Domain通常是通过参数化得到的.
P15: Morphing与Point Set Registration
这节课还是有不少干货的, 虽然算法的具体细节没有介绍, 但其思路还是给了我不少启发.
15.1 Morphing
Morphing问题通常用插值的思路去解决: 给定源模型$M^0$, 目标模型$M^1$与时间$t$, 如何计算形状$M^t$? 当$t \in [0,1]$时该问题为一个内插问题, 反之则为一个外插问题. 相关算法主要有三类,
$\cdot$ 先对一些量进行插值, 如角度, 长度, 面积, 体积或者曲率等, 如下所示.$$l^t_e = (1-t)l^0_e + tl^1_e, \\ \theta^t_e = (1-t)\theta^0_e + t\theta^1_e, \\ V^t = (1-t)V^0 + tV^1,$$其中, $l_e$为边长, $\theta_e$为两个三角形之间的二面角, $V=\frac{1}{6}\sum_{f_{i,j,k}}(x_i \times x_j) \cdot x_k$以某个三角形为底, 原点为顶点构成的椎体的体积. 最后根据这些量的插值结果恢复顶点位置, 这个算法思路也是在之前的课程中介绍过的, 通常将其转化为最优化问题, 形式如下所示.$$E_l = \frac{1}{2} \sum_e (l_e – l^t_e)^2, \\ E_a = \frac{1}{2} \sum_e (\theta_e – \theta^t_e)^2, \\ E_v = \frac{1}{2} \sum_e (V – V^t_e)^2, \\ E = \lambda E_l + \mu E_a + \nu E_v.$$$\cdot$ 对仿射变换进行插值, 常用形式是As-Rigid-Possible Shape Interpolation(即ARAP). 那么如何合理地定义$t$时刻的仿射变换$A(t)$呢? 一种最为简单的定义便是$$A(t) = (1-t)I + tA.$$显然, 这是一种线性插值, 最大的缺点便是容易在Morphing的过程中产生穿模问题. 更为合理的定义有两种, 分别是
$\quad \cdot$ 利用奇异值分解,$$A = U \sum V^T, \\ A(t) = U(t)((1-t)I + t\sum)V^T(t).$$$\quad \cdot$ 利用极分解,$$A = U \sum V^T=UV^TV \sum V^T = RS, \\ A(t) = R(t)((1-t)I + tS).$$即把仿射变换矩阵$A$分解为旋转矩阵$R$与缩放矩阵$S$, 然后分别进行线性插值.
(PS: 个人觉得此处的仿射变换应该称为线性变换更为严谨, 因为根本没有涉及平移变换吖……)
由上述定义可知, 此种算法并没有对平移变换进行处理. 因此在算法处理时, 通常还需要固定某个点的位置保持不变.
$\cdot$ 数据驱动的Morphing. 此处并非利用神经网络进行Morphing, 而是在特定的数据库中寻找$M^0, M^1$匹配的模型, 因此算法的关键便是寻找合适的衡量两个模型之间的Difference的量, 通常便是直接利用匹配顶点的位置之间的差, 如下所示.$$\bar{d}(M_i,M_j) = \sqrt{\frac{ {\textstyle \sum_{k=1}^{n}} \left \| v^i_k – v^j_k \right \| ^2 }{n} } ,$$其中, $v^i_k$是第$i$个模型$M_i$的第$k$个顶点, $n$为当前模型的顶点数量. 为了得到$M_i,M_j$之间的真正的Difference, 通常还需要进行预校准, 因为$M_i,M_j$所处的坐标系可能是不相同的, 即需要计算一个使得$M_i,M_j$之间的Difference最小的仿射变换.
上述算法结果均有可能在求解期间陷入局部最小值, 可以通过增加采样点的方式进行缓解. 即先将$[0,1]$分为$n$段, 若要求得$t$时刻($t \in (0,1)$) 的插值结果, 可将$[t/n]$时刻(此处$[x]$表示高斯函数) 的结果作为算法输入, 而非直接把源模型$M^0$作为算法输入, 相当于人为限制了优化路径. 个人还没想通为何这样的处理能缓解求解结果陷入局部最小值的现象, 但直观上来看, 能使得插值过程变得更为连续(不太严格的说法233).
15.2 Point Set Registration
点云注册的目的是为了把两个不同的点集放至相同的坐标系中, 其中最经典的算法便是Iterative Closest Point算法(ICP), 通常会将其转化为最优化问题进行求解, 即要极小化下述能量函数,$$E(P,Q) = \sum_{(p_i,q_i)} \left \| Rp_i + t – q_i \right \| ^2_2.$$这个能量函数的优化过程还是十分巧妙的, 详细推导可参考视频内容.
P16: Atlas Generation
本节课包含本人许多比较感兴趣的点, 其中涉及到的论文也多数是自己曾经看过或者计划想看的, 因此会尽可能记录下本节课介绍的重点内容. Atalas的生成算法通常包含三步, 分别是Mesh Cutting, Chart Parameterizations与Chart Packing, 主要应用于信号存储与几何处理等领域. 本节课仅介绍了前两步, 最后一步Packing在本节中仅作简单介绍, 具体内容的介绍留待下节.
16.1 Mesh Cutting
Mesh Cutting这一步的目标是算法结果的扭曲程度尽可能低, 且割线长度尽可能小. 扭曲程度尽可能低的目标是容易理解的, 而割线长度尽可能小的目标则是因为在进行完Mesh Cutting这一步以后, 若想进行颜色编辑, 需要保证割线两边的颜色差异尽可能地小, 否则在网格渲染出来以后, 割线就会较为明显地呈现在网格上. 因此, 割线长度尽可能小的算法结果能使得颜色编辑的流程更为顺畅. Mesh Cutting的实现方式主要有两类.
$\cdot$ Points $\to$ Paths. 其思路很简单: 找出引起高扭曲的点, 然后把这些点在网格表面上连起来(一般为测地线), 则得到相应的网格割线. 代表论文便是顾险峰老师于Siggraph 2002上发表的Geometry Images, 这篇论文也是自己一直很想看的一篇论文, 只可惜一直没能抽出时间来. 傅孝明老师这里也简单地介绍了一下这篇文章的算法思路: 主要采用了迭代法, 首先在网格上随机选取一条割线, 将原来的闭网格转化为一个开网格, 利用Tutte’s Embedding将开网格参数化为平面上固定边界(一般为圆周) 的网格, 找出引起高扭曲的割线, 将其添加到初始割线中, 接着重复上述步骤, 不断扩展割线, 直到得到的参数化网格内(除去边界) 不再含有引起高扭曲的点. 但该算法有一些较为明显的缺点:
$\quad$ $\cdot$ 受初始值的影响较大, 一个缓解该问题的方案为, 在找到两个引起高扭曲的点以后, 把初始割线从当前割线中移除, 再把这两个点连成的割线作为初始割线继续执行算法即可.
$\quad$ $\cdot$ 若算法进行过程中引起高扭曲的点基本都落在平面网格边界上, 则算法会过早地提前结束, 尤其在处理较为圆滑的网格时这个问题将会表现得更为明显.
$\quad$ $\cdot$ 算法得到的割线无法保证全局最优.
$\cdot$ Segmentation. 代表论文是发表于EG 2015的D-Charts: Quasi-Developable Mesh Segmentation, 其算法目标是将网格分割为若干块$C$, 使得每一块$C$的参数化结果的扭曲程度尽可能低, 其中每一个块$C$”接近”一个可展曲面(Developable Surface, 即每一点处高斯曲率为零的曲面, 能够经弯曲而展开成一片平面). 由于可展曲面的类型很多, 因此文章选取的目标可展曲面是一类最简单的可展曲面——直纹曲面(每一点处法向与其轴的夹角为常数的曲面), 并称之为Proxy(< axis, angle >, <$N_C,\theta_C$>), 而衡量块$C$与Proxy之间的距离的能量函数则定义为$$F(C,t)=(N_C \cdot n_t, – cos\theta_C)^2,$$其中$t$为块$C$中的三角形. 文章的算法步骤如下所示(采用Lloyd算法的思想):
$\quad$ 1) 随机选取三角形作为种子”点”.
$\quad$ 2) 利用贪心算法往种子点周围扩张形成块$C$.
$\quad$ 3) 在每一块$C$上选取新的Proxy($F(C,t)$应保证有界).
$\quad$ 4) 重复第2, 3步直至算法收敛.
$\quad$ 5) 在上述Lloyd算法结果的基础之上进行洞的填补, 其中小洞则直接与邻居块$C$合并, 大洞则作为一个新的块$C$.
$\quad$ 6) 合并不同的块$C$, 尽可能地减少块$C$的数目, 合并准则为合并后的$F(C,t)$在可接受的范围内.
$\quad$ 7) 后处理与参数化.
其中, 第3步中需要优化下述能量函数,$$\min_{N_C,\theta_C} \frac{1}{A_C} {\textstyle \sum_{t \in C}} A_tF(C,t), s.t. \left \| N_C \right \| =1.$$
16.2 Chart Parameterizations
Chart Parameterizations这一步的目标是构造双射(算法结果的边界不会自交) 使得算法结果的等距扭曲程度尽可能低, 代表论文主要有三篇, 其中最后一篇是中科大组内的Siggraph文章, 仅仅是简单介绍了一下, 此处便不作记录.
$\cdot$ Bijective Parameterization with Free Boundaries, Siggraph 2015. 核心思想是定义了关于边界点$U_i(i \ne 1,2)$与其它边界(两端端点不妨设为$U_1, U_2$)的障碍函数:$$max(0,\frac{\varepsilon}{dist(U_1,U_2,U_i)}-1)^2,$$其中$dist(U_1,U_2,U_i)$衡量了一个边界点$U_i(i \ne 1,2)$到边界$(U_1,U_2)$的距离. 此处障碍函数中平方的作用可能是为了简化求导的过程.
$\cdot$ Simplicial Complex Augmentation Framework for Bijective Maps, Siggraph Asia 2017. 文章中使用了一种被称为脚手架的平面网格结构, 将经Tutte’s Embedding得到的初始平面网格与脚手架平面网格作为一个整体, 并将这个整体限制在一个Bounding Box里. 那么在算法的优化过程中, 外边界显然是保持不动的, 即不会发生自交, 因此对于内部网格, 仅需保证三角形无翻转即可得到边界不自交的结果. 文章算法的主要缺点在于, 算法进行的过程中脚手架网格中的三角形有可能发生翻转, 此时需要对脚手架网格进行Remesh, 这样一来就会改变三角形的数目或者连接关系, 从而求解所用的Hessian矩阵的非零元结构也在不断地发生改变, 导致较大的时间开销.
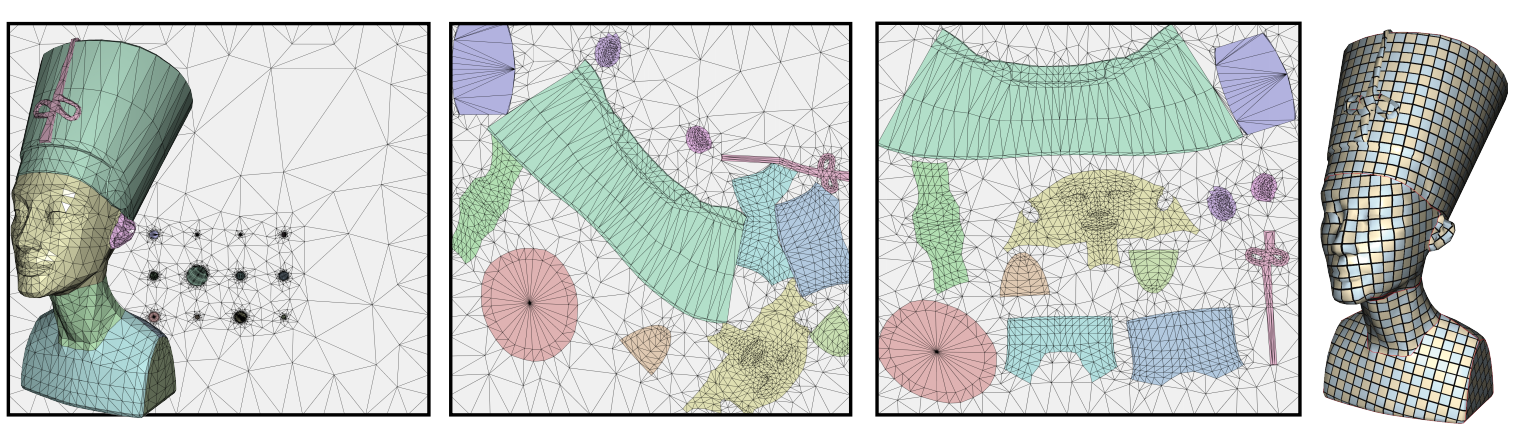
16.3 Chart Packing
Chart Packing这一步的目标是算法结果的Packing效率尽可能地高, 即网格在贴图上对应的块的面积总和与贴图面积的比值尽可能地接近1.
P17: Chart Packing与Simplification
本节介绍的内容自己都挺感兴趣的, 只可惜傅孝明老师介绍的知识点还是偏入门, 干货相比较上节课来说还是少一些的.
17.1 Chart Packing
主要介绍了傅孝明老师与刘利刚老师于Siggraph 2019上合作发表的文章, Atlas Refinement with Bounded Packing Efficiency. 目前与Chart Packing相关的算法的主要目标均非提升PE(Packing Efficiency), 而是针对其它约束, 如扭曲程度较低, 各三角面片朝向一致, 网格无自交, 割线长度较短等, 这也是傅孝明老师这篇文章的亮点之一. 算法流程如下图所示,
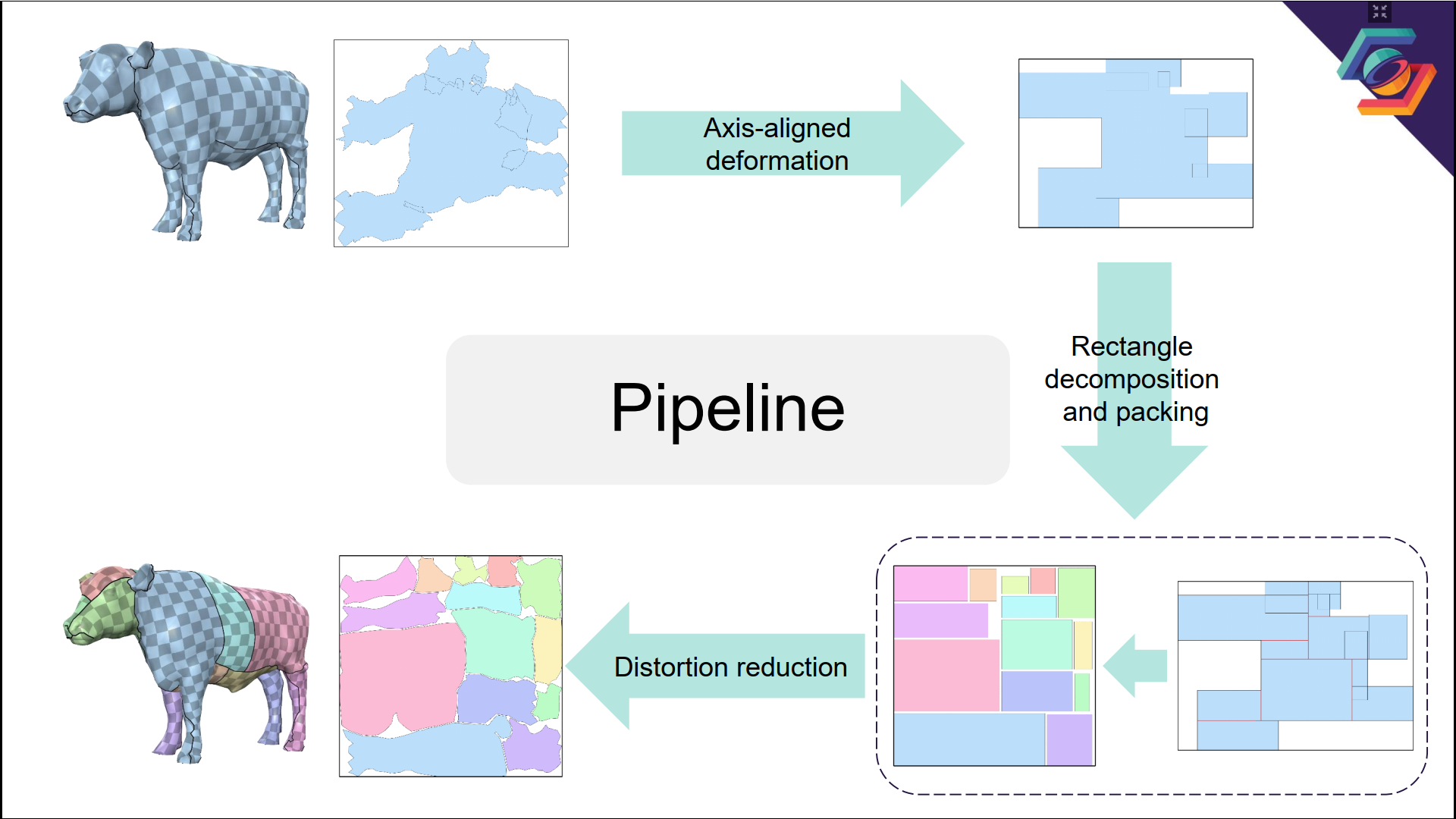
老师并没有介绍的具体的算法细节, 包括自己更感兴趣的PE下确界证明=.= 因此这里也不再介绍, 等日后有空再仔细阅读一下这篇论文. PS: 文章算法第一步的思想其实类似于前面介绍的PolyCube的相关算法思想.
17.2 Simplification
$\cdot$ Defination与Local Operations. Simplification是把一个给定的多边形网格转化为一个含有更少的点, 线与面的网格的操作, 也是一种在游戏开发中应用十分广泛的技术(如LOD). 其蕴含的Multi-Resolution思想也是解决许多几何处理问题的常用思路, 即把在低分辨率网格上的结果迁移至高分辨率网格上.
由于许多Simplification算法是迭代进行的, 即它们通过每次移除一个顶点来实现逐步简化, 因此许多Simplification算法通常是可逆的(如Hierarchical Method), 而每次移除一个顶点的过程则称之为一个局部操作(Local Operation). 局部操作的方式通常有Vertex Removal, Edge Collapse, Half-Edge Collapse等三种, 其中Edge Collapse与Half-Edge Collapse在拓扑上是一致的, 区别只是经Collapse以后得到的新顶点的位置会有所不同.
$\cdot$ Quadric Error Metric(简称QEM). 首先不妨来看看平面$P_i = (x_i, n_i)$上的QEM是如何定义的: 点$x$到平面$P_i$的距离的平方为$$d(x,P_i) = (n^T_ix – d_i)^2,\\d_i = n^T_ix_i.$$采用齐次坐标的形式记$\bar{x} = (x, 1), \bar{n_i} = (n_i, -d_i)$. 则$$d(x, P_i) = (\bar{n_i}^T\bar{x})^2 = \bar{x}^T\bar{n_i}^T\bar{n_i}\bar{x} =: \bar{x}^TQ_i\bar{x}.$$而顶点$v_i$上的QEM则定义为$$Q^T_i = \sum_{j \in \Omega(i)}Q_j.$$边$e$上的QEM定义为$$Q^e = Q^v_1 + Q^v_2.$$这样一来, 每一次局部操作可以转化为一个最优化问题:$$\bar{v} = arg \min_{v} v^TQ^ev,$$其中, $Q^e$不一定是一个满秩矩阵, 当$Q^e$满秩时可直接采用最小二乘法求解, 而当$Q^e$不满秩时则最小二乘法无法生效了(最小奇异值为0), 此时取边$e$上的中点作为当前最优化问题的近似解即可. 同时定义新顶点$\bar{v}$上的QEM为$Q^e$. QEM算法伪代码如下图所示,

$\cdot$ Variational Shape Approximation(VSA). VSA是一种使用平面逼近多边形网格的技术, 与前面介绍的Atlas Generation中的Segmentation思想比较类似. VSA本质上便是一种Segmentation方法, 只是使用的代理(可展曲面) 被严格限制为平面. VSA所研究的问题为: 给定$k \in N$, 三角网格$M$与误差度量$E$($L^2$或$L^{2,1}$), 寻找一个区域集$R = \{ R_1, \cdots, R_k \}$与一个代理集$P = \{ P_1, \cdots, P_k \}$使得下述关于扭曲程度的能量函数最小,$$E(R, P) = \sum^k_{i=1}E(R_i, P_i),$$其中,$$R_1 \cup \cdots \cup R_k = M,\\P_i=(x_i, n_i), i \in \{ 1, \cdots, k \},$$而$R_i$与$P_i$之间的误差度量有两种定义方式, 分别为
$\quad \cdot$ $L^2$误差:$$L^2(R_i, P_i) = \int_{x \in R_i}(n^T_ix – n^T_ix_i)^2dx.$$$\quad \cdot$ $L^{2,1}$误差:$$L^{2,1}(R_i, P_i) = \int_{x \in R_i}\left \| n(x) – n_i \right \|^2 dx.$$其中, 通过$L^2$误差得到的代理$P_i$为一个最小二乘拟合平面, 而通过$L^{2,1}$误差得到的代理$P_i$的法向为输入网格$M$的所有面法向的加权平均值. 求解上述优化问题通常采用Lloyd算法.
P18: Spherical Parameterizations
球面参数化是一个亏格为0的闭曲面与球面之间的同胚, 其约束主要有三点, 分别为球面约束($x^2+y^2+z^2=r^2$, 这是一个非线性且非凸的约束), 双射约束(可根据实际情况弱化为无翻转三角形的约束) 与低扭曲的约束. 在球面参数化领域, 最大的挑战主要有两个: 一个是无法使用Tutte’s Embedding Method, 因为球面是一个闭曲面; 另外一个则是待求解的最优化问题是非线性与非凸的. 相关算法主要有两类, 其实本节最后还提及了曲率流的相关算法, 但仅是几句话带过, 故此处亦不作过多记录.
$\cdot$ Hierarchical Method. 代表论文为Advanced Hierarchical Spherical Parameterizations, 其算法流程如下图所示,

其中, (a)-(d)对应的过程称为Decimation(即减面), (e)-(g)对应的过程称为Refinement(即细分). 本节重点介绍了Decimation过程, Refinement过程讲得十分模糊(细节可以参考文章Progressive Embedding附录中的Vertex Split一节). 在Decimation的过程中, 主要执行了去除高曲率区域的Simplicafation操作, 所使用的Curvature Error Metric(CEM) 定义如下,$$E^C_{jk}=\frac{g(V_j)}{d_e(V_{kj}) \cdot \rho (V_{kj})},$$其中, 各符号定义如下,
$\quad \cdot$ $g(V_j)$是顶点$V_j$上的高斯曲率;
$\quad \cdot$ $d_e(V_{kj}) = e^{(d(V_{kj})-6)^2}$, 顶点$V_{kj}$是由顶点$V_k$与顶点$V_j$坍缩得到的新顶点, $d(V_{kj})$是顶点$V_{kj}$的度;
$\quad \cdot$ $\rho(V_{kj}) = \sum_{f \in \Omega(V_{kj})} \frac{c_r(f)}{2 \times i_r(f)}$, $f$为顶点$V_{kj}$连接的面, $c_r(f)$为面$f$的外接圆半径, $i_r(f)$为面$f$的内切圆半径. 当$f$恰为正三角形时, $\frac{c_r(f)}{2 \times i_r(f)} = 1$, 否则一般大于1.
从上述定义易知, 当顶点曲率越高或者顶点周围的三角面形状越”偏离”正三角形, 该顶点越容易在Decimation的过程当中被移除. 此外, 若想在Decimation的过程当中执行去除低曲率区域的Simplicafation操作, 仅需将上述CEM取倒数以后作为新的CEM即可.
若Refinement过程的输入网格包含较多高曲率区域, 则会极大地影响参数化结果的顶点分布(非均匀分布). 因此Decimation过程通常使用Flat-to-Extrusive Decimation策略: 先通过QEM进行Simplification, 再通过CEM去除高曲率区域.
$\cdot$ Two Hemisphers. 流程如下图所示:

即把一个亏格为0的闭曲面一分为二变成两个开网格, 如此一来可以利用Tutte’s Embedding与球极投影分别映射到两个半球面上, 最后将两个半球面上的参数化结果拼接起来即可, 如下图所示. 其中, 从(b)到(c)的过程中, 算法利用了复变函数$f(z) = \frac{1}{\bar{z}}$的性质, 将单位圆内的点映射至单位圆外, 这是个很有意思的点.

算法存在两个问题, 分别是
$\quad \cdot$ 如何选择割缝? 算法使用了Metis库(这也是UE5的Nanite所使用到的库, 未来也许值得研究), 将输入网格划分为顶点数目大致相当的两部分.
$\quad \cdot$ 如何将平面上的参数化结果迁移至球上?
$\quad \quad \cdot$ Moebius Inversion$f(z) = \frac{1}{\bar{z}}$, 该函数可将单位圆内的点映射至单位圆外.
$\quad \quad \cdot$ 使用球极投影将结果映射至单位球上, 形式如下:$$P(u,v) = \frac{1}{1 + u^2 + v^2}(2u, 2v, 1 – u^2 – v^2).$$
P19: Directional Field
19.1 Introduction
方向场是一个点的集合, 其中每个点不仅包含位置信息, 还包含特定的方向信息, 常见的方向场有法向场, 曲率场等. 具备旋转对称性的方向场称为旋转对称方向场(Rotationally-Symmetric Directional Field, 简称RoSy场), 即其上每个点的方向之间的角度可能是固定的, 常见的RoSy场如下图所示.

观察上图可以发现, 对于$a^b$-Vector(Directional) Field中每个点上的$a \times b$个方向, 可将其分为$b$个组, 每个组内含$a$个方向, 且每个组内的相邻方向相对于平面上某个轴的角度均相差$2 \pi / a$. 其中, 4-Directional Field又被称为Cross Field, $2^2$-Vector Field又被称为Frame Field, 是经常使用的两个方向场.
从方向场的角度来看, 等距参数化其实也是一个方向场的拟合过程, 回顾P6 6.1中提到的LSCM算法, LSCM定义了一个能量函数, 该能量函数描述了当前网格每个三角面片上的Jacobi矩阵($2 \times 2$) 与目标旋转矩阵的距离, 此时目标旋转矩阵可以看成是两个相互正交的列向量的组合, 极小化该能量函数的过程亦是一个方向场的拟合过程. 除了在参数化领域的应用之外, 网格生成, 六面体网格化, 变形, 纹理映射与建筑几何等领域也都能见到方向场的身影.
19.2 Discretization
本小节介绍的概念是为了得到网格上”连续”的方向场. 首先介绍了切空间的定义, 此处并不纠结于切线与副切线的计算, 因此相比较渲染中的切空间, 理解难度还是低很多的. 在进行两个相邻切空间的方向场比较前, 需要建立两个切空间之间的Connection, 最常用的Connection是Levi-Civita Connection, 建立的方法也十分简单, 直接将其中一个切空间进行旋转, 直至其法向与另外一个切空间的法向一致即可. 从参数化的角度来看, 这个操作也是一种局部参数化, 结果便是将两个相邻的切空间摊平到同一个平面上, 从而方向场的比较能在同一个坐标系下进行.
接下来定义了方向场中的奇异点, 即该点处的方向不是Well-Defined的, 用指标的语言描述即指标为0的点.
$\cdot$ 连续方向场中点$p$的指标定义如下,$$index_p = \frac{1}{2\pi}(\alpha(1) – \alpha(0)),$$$\alpha$通常是连续的, $\alpha(1) – \alpha(0)$唯一且恰为$2\pi$的倍数. 且由Poincare-Hopf定理知闭曲面上的向量场上的所有点的指标之和为$2-2g$, 其中, $g$为闭曲面的亏格.
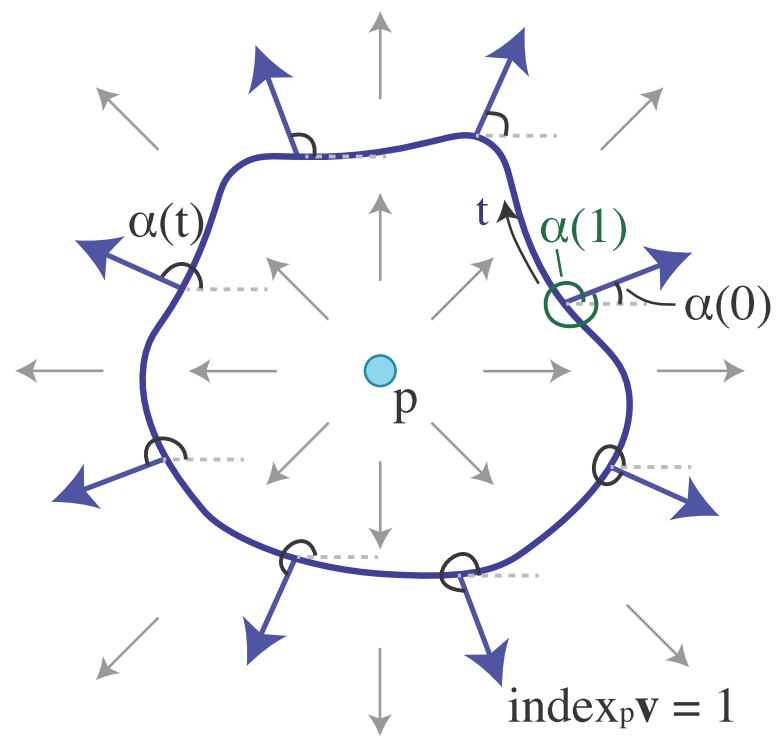
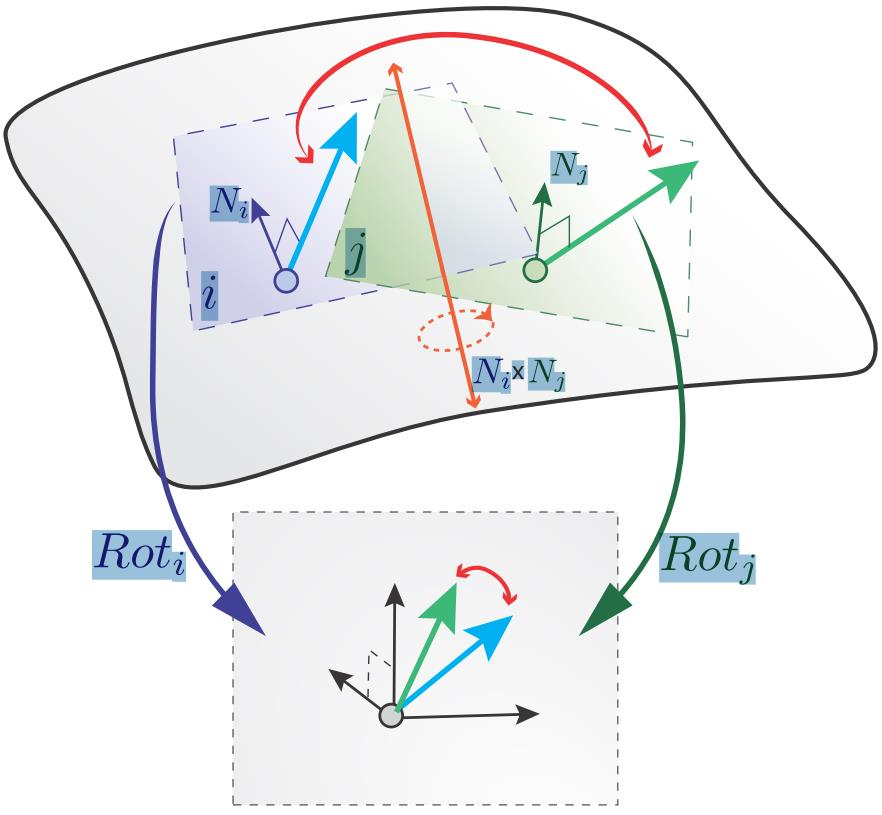
$\cdot$ 离散$N$-RoSy场中, 对于三角网格上的同一个面而言, 其上每个点的方向都是一致的(均与当前面平行), 奇异点仅能出现在边上. 此时点$p$的指标定义如下,$$index_p = \frac{1}{2\pi} \sum (\delta_{ij} + 2\pi k),$$其中, $k \in N$称为Period Jump, $\delta_{ij} \in [-\pi, \pi)$是经建立Levi-Civita Connection后切空间$X_i$与切空间$X_j$($p \in X_i \cap X_j$) 对应方向的旋转角度(对应方向的旋转角度都是一样的?), 如下图所示. 需要注意的是, $\delta_{ij}$会受切空间$X_i$与切空间$X_j$的对应方向的选取方式的影响, 在不同的选取方式之间, 不同的$\delta_{ij}$将相差$2\pi k / N, k \in N$, 通常选取的$k$值需要使得$\delta_{ij}$最小.
19.3 Representation
由上述讨论整理可得, 离散$N$-RoSy场中, 设切空间$X_i$与切空间$X_j$上的局部标架分别为$\{ e_{i1}, e_{i2}\}, \{ e_{j1}, e_{j2}\}$, 则$X_i$与$X_j$之间的$\delta_{ij} \in [-\pi, \pi)$可定义如下$$\delta_{ij} = \phi_j – (\phi_i + X_{ij} + \frac{2\pi}{N}k_{ij}),$$其中, $\phi_i$为$X_i$中任一点$x_i$上的指定方向相对于$e_{i1}$的带符号旋转角度, $X_{ij}$为经建立Levi-Civita Connection后切空间$X_i$与切空间$X_j$($p \in X_i \cap X_j$) 对应坐标轴的旋转角度, $k_{ij} \in N$为Period Jump. 易知, 使用Period Jump可以使得建立的模型清晰易懂, 但也引入了整数规划问题.
为了规避整数规划问题, 也有学者使用三角函数的形式表示方向, 即$v=(cos\phi, sin\phi)^T = e^{i\phi}$, 如此一来便可规划Period Jump的使用, 但也同样引入了非线性优化问题, 因此这种表示方法也并不常用. 目前更被认可的表示方法是复数多项式.
对于$N$-向量集$\{ u_1, \cdots, u_N \}, u_i \in C$, 可得其对应的复数多项式$$p(z) = (z – u_1)\cdots(z – u_N) = {\textstyle \sum_i^N } c_iz^i,$$则其系数集$\{ c_i \}$是一个2维向量的顺序无关的表示. 使用复数多项式表示离散$N$-RoSy场的一个最大的优点便是用幂运算规避了整数规划问题: 相邻的$u_i, i \in [1,\cdots,N]$的相对于特定坐标轴的旋转角之间总是相差$\frac{2\pi}{N}$, 则对于$\forall i \in [1,\cdots,N]$, 将$u_i$旋转$\frac{2\pi}{N}$若干次以后总能得到一个特定的$u_k, k \in [1,\cdots,N]$, 不妨用$u_1$表示其它$u_i, i \ne 1$, 则$p(z) = z^N + \cdots + (-1)^Nu_1^N$, 显然规避了整数规划问题. 这样一来, 比较两个切空间上的离散$N$-RoSy场, 仅需比较对应的复数多项式系数集$\{ c_i \}$即可.
P20: Directional Field中的Objectives and Constraints
20.1 Objectives
在不同的应用领域中, 通常会使用不同的能量函数用于优化方向场, 所期望得到的方向场的性质也会有所不同, 如光滑性, 平行性, 正交性与旋度极小性等. 以平行性为例, 其能量函数通常设置为如下形式:$$E_{fair-N} = \frac{N}{2} \sum_e w_e(\delta_e)^2.$$当使用的方向场为Cross Field时, 上述能量函数即可写为$$E_{fair-4} = \frac{4}{2} \sum_e w_e(\phi_j – (\phi_i + X_{ij} + \frac{2\pi}{N}k_{ij}))^2,$$其中各符号含义详见上节, 此处不再赘述.
由于$k_{ij}$为整数, 上述最优化问题的求解难度是比较大的. 一种常用的贪心算法为:
1. 将$k_{ij}$视为实数, 再极小化$E_{fair-4}$.
2. 对上述步骤求得的$k_{ij}$进行取整(如四舍五入).
3. 重复上述两步.
当然也可以使用上节介绍的复数多项式表示, 来规避整数$k_{ij}$带来的整数规划问题. 但需要注意的是, 若使用复数多项式表示上述最优化问题, 且不加约束, 求得的各个面上的方向场中容易出现退化的情况(方向全为0), 因此在求解上述最优化问题时, 需要确定两个面上的方向场, 以此作为约束.
20.2 Constraints
求解方向场的过程中常见的约束主要有三种.
$\cdot$ 对齐约束. 即求得的方向场中的方向需要与预定义的方向对齐, 预定义的方向可以从主曲率, 边界, 特征线或者用户自定义的曲线中得到.
$\cdot$ 对称约束. 若网格表面具有双边对称性, 则求得的方向场也应遵循相同的对称性.
$\cdot$ 曲面映射约束. 对两个具有对应关系的网格, 其方向场也应具有对应关系.
20.3 Integrable field
不妨将一个网格表面上的连续方向场视为网格表面上的一个连续多值函数, 该多值函数的值域维度为$n$, 将该多值函数”拆分”为$n$个实值函数, 若这$n$个实值函数均在网格表面上可积, 则称该连续方向场为一个可积场. 一个常见的可积场为参数化过程中使用的方向场的梯度场, 该方向场对应的两个标量函数均在每个网格顶点上是Well-Defined的. 可积场也提供了另外一个参数化的思路, 即将优化得到的梯度场进行积分, 即可得到参数化结果.
可积的一个充要条件是旋度为0(无旋, 该充要条件待求证). 对于任意标量函数$h:M \to R$, 有$$\left \langle \nabla h_f,e \right \rangle = \left \langle \nabla h_g,e \right \rangle,$$其中, $f,g$为两个相邻的三角形, 其公共边为$e$. 则对于任意1-Vector Field $\alpha$, $\alpha$无旋的充要条件为$\left \langle \nabla \alpha_f,e \right \rangle = \left \langle \nabla \alpha_g,e \right \rangle.$
$\cdot$ Cross Field的无旋化
论文Computing Inversion-Free Mappings By Simplex Assembly中使用了这样一个能量函数$$E = E_C + \lambda E_{Field},\\E_{Field} = \sum_e (\left \langle \alpha_f,e \right \rangle – \left \langle \alpha_g,e \right \rangle)^2 + (\left \langle \beta_f,e \right \rangle – \left \langle \beta_g,e \right \rangle)^2,$$其中, $E_C$是一个与扭曲程度相关的能量函数. 算法进行的过程中, 会逐步增加$\lambda$, 使得在最终的优化结果中$E_{Field}$趋近于0. 然而, 算法结果并不能保证网格上每个点上的两个方向是正交的, 我们可以将两个方向分别往反方向延伸, 这样便得到了一个Frame Field, 如下图所示. 这样一来, 我们便将Cross Field无旋化的问题转化为Frame Field无旋化的问题.
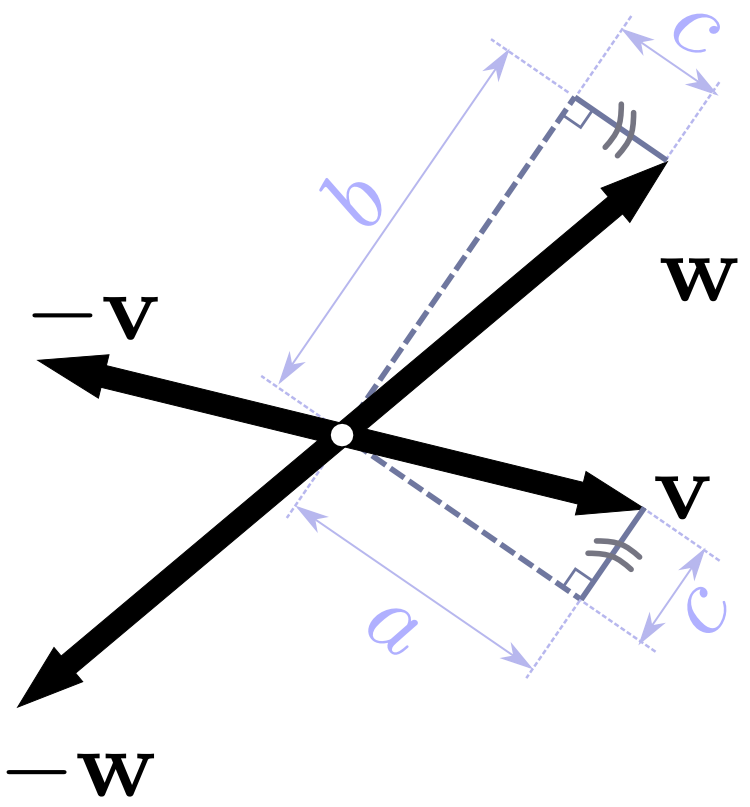
论文Frame Fields: Anisotropic and NonOrthogonal Cross Fields提供了一种Frame Field无旋化的算法. 作者从列向量组的角度出发, Cross Field(4-RoSy Field) 上每个点的方向集可以写为$X = \left \langle u, u^\bot, -u, -u^\bot \right \rangle$, 而Frame Field($2^2$Vector Field) 上每个点的方向集则可以写为$F = \left \langle v, w, -v, -w \right \rangle$. 不妨将$F$视为一个矩阵, 则可以对$F$使用极分解得到$F = WX$, 其中$W$是一个对称正定矩阵(Symmetric Positive Definite Matrix, 简称SPD Matrix). 极分解可以采用SVD得到, 即$F = U \sum V^T = $$ U \sum U^T UV^T$, 令$W = U \sum U^T, X = UV^T$,即可得到$F$的极分解. 作者认为, 若$X, W$对于网格表面上的点均为连续函数甚至光滑函数, 则该Frame Field也是一个连续向量场甚至光滑向量场.因此, 分别优化$X, W$即可得到无旋的Frame Field.
$\quad \cdot$ $X:$ 采用之前的能量函数进行优化, 即$$E_{fair-4} = \frac{4}{2} \sum_e w_e(\phi_j – (\phi_i + X_{ij} + \frac{2\pi}{N}k_{ij}))^2.$$
$\quad \cdot$ $W:$ 采用拉普拉斯光顺算子, 由于拉普拉斯光顺算子是一个凸组合的形式, 故能保证光顺后的$W$仍旧为一个SPD矩阵.
$\cdot$ $2^2$方向场的无旋化
论文General Planar Quadrilateral Mesh Design Using Conjugate Direction Field提供了一种$2^2$方向场无旋化的算法. 作者依旧从列向量组的角度出发, $2^2$方向场上每个点的方向集可以写为$F = \left \langle v, w, -v, -w \right \rangle$, 其中$\left \| v \right \| = \left \| w \right \|$. 等价的写法还有: $F = \left \langle w, -v, -w, -v \right \rangle$, $F = \left \langle -v, -w, v, w \right \rangle$, $F = \left \langle -w, v, w, -v \right \rangle$. 它们之间相差如下带符号的置换矩阵:$$\begin{pmatrix}1 & 0\\0 & 1\end{pmatrix},\begin{pmatrix}0 & 1\\-1 & 0\end{pmatrix},\begin{pmatrix}-1 & 0\\0 & -1\end{pmatrix},\begin{pmatrix}0 & -1\\1 & 0\end{pmatrix}.$$故在比较相邻面的方向场时, 使用的度量应为:$$[v_f | w_f] = [v_g | w_g]P_{fg},$$其中, $f,g$为相邻的两个面, 其公共边为$e$, $P_{fg}$是上述四个置换矩阵所构成的集合中的元素. 实际上, 此处引入置换矩阵的初衷与离散$N$-RoSy场中引入整数变量$k_{ij}$的初衷是一致的, 均是为了规避人为选择顺序的影响, 只不过此处讨论的对象为$2^2$方向场, 每个点上的各方向间的夹角并不是固定的90度, 因此此处需要使用置换矩阵的语言进行描述. 论文的算法思想也可以推广至3维情形.
P21: Remeshing
从这一节开始介绍的内容很多都与自己硕士阶段研究的内容有关, 所以还是挺有亲切感的. 重新网格化是一种提升网格质量的关键技术, 其目标有两个:
$\cdot$ 输入网格与输出网格应在某些指标(如位置, 法向, 曲率等一些高阶微分量) 上尽可能相似.
$\cdot$ 提升输入网格的质量, 不同的应用对于输入网格一般会有不同的要求.
算法输入一般是三角网格, 而用于衡量网格质量的因素也有很多, 如采样密度, 奇异点数量(三角网格中一般认为度不为6的点为奇异点, 但奇异点对于渲染的影响程度一般较小), 顶点数量, 网格朝向(各向同性与各向异性), 对齐质量(如网格元素与特征线的对齐程度), 网格元素的形状与拓扑性质等.
21.1 Incremental Remeshing
在重新网格化领域, 一种经典算法是Incremental Remeshing. 它主要包含四种操作, 如下图所示.
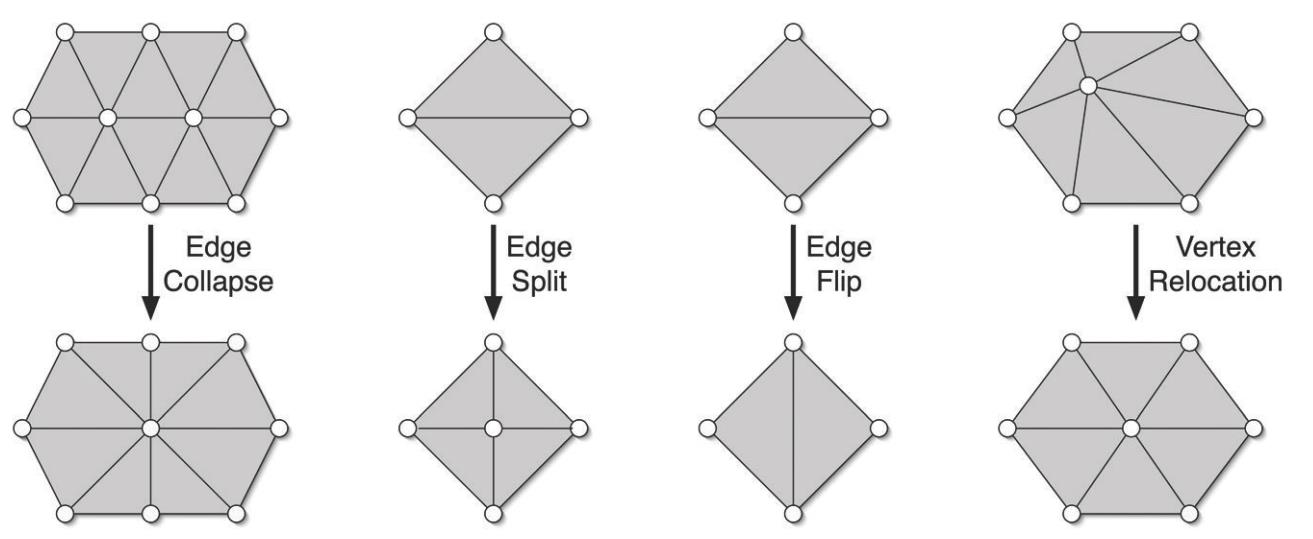
算法伪代码如下所示:

接下来解释算法各步骤.
$\cdot$ 算法中使用了两个经验参数$\frac{4}{5},\frac{4}{3}$.
$\cdot$ Split long edges(high_e). 遍历当前网格中的所有边, 遍历过程中若发现某条边的长度大于给定的阈值high_e, 则将这条边从中点”劈开”, 使得两个相邻的三角形被平分.
$\cdot$ Collapse short edges(low_e, high_e). 塌陷所有长度小于给定阈值low_e的边. 但这种局部操作带来的问题是, 随着短边的塌陷, 可能引入长度大于给定阈值high_e的长边. 解决这个问题的方法是在每次塌陷之前测试此次塌陷操作是否会引入不合法的长边, 若会引入, 则不执行本次塌陷操作.
$\cdot$ Equalize valences. 通过翻转边使得顶点的度相等(三角网格中顶点的目标度通常设置为6), 判断是否能进行翻转的准则通常可以设置为如下形式:$$\sum_{i} |degree(v_i) – 6|,$$其中, $i$为受到本次翻转边影响的顶点的下标, $degree(v_i)$为顶点$v_i$的度. 若本次翻转边后, 该值减少, 则认为可执行本次翻转边的操作.
$\cdot$ The tangential relaxation. 对网格进行光顺, 光顺通常使用拉普拉斯算子,$$q = \frac{1}{N_p} \sum_{p_j \in \Omega(p)} p_j.$$若光顺过程中有顶点$p$偏离网格表面, 则需要将偏离的顶点$p$重新投影至网格表面上点$q$的切平面上,$$p’ = q + nn^T(p-q).$$
当对算法结果有保特征的要求时, 算法执行过程中要注意以下几点.
$\cdot$ 特征线与特征点均已在输入模型中作出标记.
$\cdot$ 所有局部操作应保持角点(超过2条特征边连接或者只连接一条特征边的点) 不动.
$\cdot$ 特征点应沿着特征线塌陷.
$\cdot$ 分割一条特征边会引入两条新的特征边与一个新的特征点.
$\cdot$ 特征边不应被翻转.
21.2 Parameterization-Based Method
除了Incremental Remeshing以外, 还可利用参数化将三维空间上的重新网格化问题转化为二维平面上的重新网格化问题. 相比较三维空间, 我们更容易调整二维平面上的采样点的位置. 但这种方式也会带来几个问题.
$\cdot$ 参数化结果通常带有扭曲.
$\cdot$ 当一个网格切割(使得切割产生的块与圆盘同胚) 后其参数化结果容易产生不连续点.
$\cdot$ 当处理的网格的隐藏曲面为闭曲面时, 通常需要对网格进行切割. 因此, 割缝的质量十分重要. 常用的生成割缝的算法上文已介绍, 如D-Charts算法. 但在分别对各块进行重新网格化以后, 边界可能出现拼接不上的问题, 常用的解决方案是不对上一块的边界进行处理, 将其边界与下一块一并重新网格化.
尽管有上述缺点, 但基于参数化的算法能够避免Incremental Remeshing在重投影步骤出现异常的问题, 因此还是被许多学者所认可.
21.3 Approximation
重新网格化希望输入网格与输出网格应在某些指标(如位置, 法向, 曲率等高阶微分量) 上尽可能相似, 而通常用于衡量两个网格的顶点位置的差异的度量便是Hausdorff距离. 在拓朴学上, Hausdorff距离用于衡量两个度量空间的子集彼此之间的距离.
Hausdorff距离 令$X, Y$是度量空间$(M,d)$的两个非空子集. 我们定义Hausdorff距离$d_H(X, Y)$为$$d_H(X, Y) = max\{ \sup_{x \in X} \inf_{y \in Y} d(x, y), \sup_{y \in Y} \inf_{x \in X} d(x, y) \}.$$一般来说, $\sup_{x \in X} \inf_{y \in Y} d(x, y) \ne \sup_{y \in Y} \inf_{x \in X} d(x, y),$ 如下图所示.
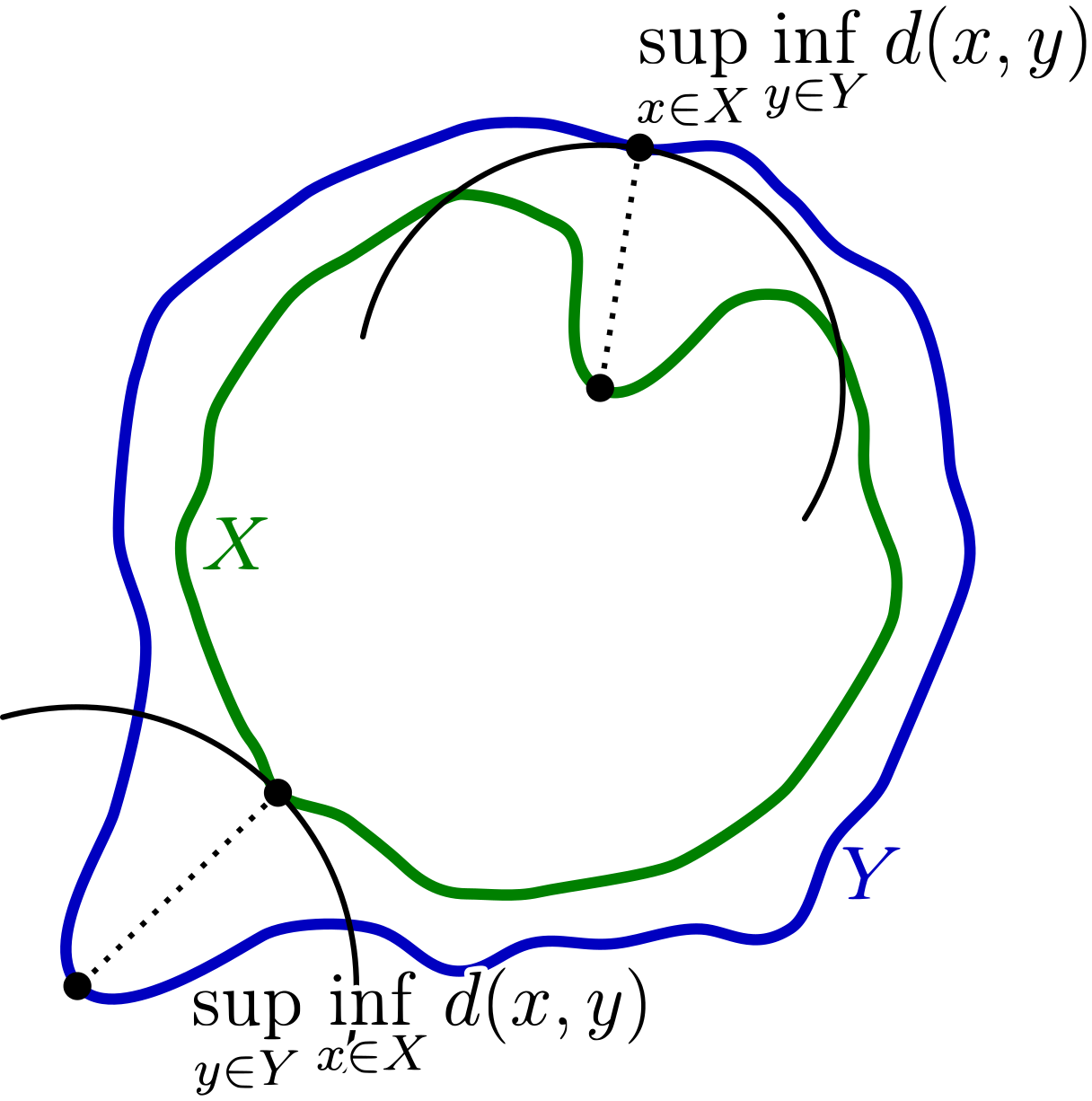
当把Hausdorff距离推广至三角网格上以后, 此时三角网格$M_1, M_2$之间的Hausdorff距离定义为:$$d_H(M_1, M_2) = \max \{ d_h(M_1, M_2), d_h(M_2, M_1) \},$$其中$d_h(S, T) = \max_{p \in S} \min_{q \in T} d(p, q) := \max_{p \in S} d(p, T).$
实际上, 计算两个三角网格$M_1, M_2$之间的Hausdorff距离的计算量是比较大的, 因此通常需要进行近似. 对$M_1, M_2$分别进行采样得到两个点集$S_1 \subset M_1, S_2 \subset M_2$, 则$d_h(M_1, M_2)$可被近似为$$d_h(M_1, M_2) \approx \max_{a \in S_1} d(a, M_2)\\\Longrightarrow d_H(M_1, M_2) \approx \max \{ \max_{a \in S_1} d(a, M_2), \max_{b \in S_2} d(b, M_1) \}.$$上述计算方式对于$d_H(M_1, M_2)$的逼近程度是高于直接计算$d_H(S_1, S_2)$的.
21.4 Error-Bounded Method
这是在2007年便已经提出的一种算法, 其主要的算法思想是若当前的局部操作会使得当前网格与输入网格之间的Hausdorff距离大于给定的阈值, 则不执行当前的局部操作, 从而使得当前网格始终处于一个Error-Bounded的可行集里. 说实话, 我一直以为Error-Bounded Method是从理论上证明有界, 非常期待看到相关证明. 事实证明, 是我想太多了……
这种算法存在一个关键的问题便是, 每进行一次局部操作前都要计算Hausdorff距离的代价太高了, 因此有学者提出, 不需要每进行一次局部操作前都计算Hausdorff距离, 可以在固定次数的局部操作以后, 检查当前网格与输入网格之间的Hausdorff距离是否大于给定的阈值. 若是则往导致Hausdorff距离较大的区域进行插入点的操作, 实验证明, 当插入的点使得当前区域的点的分布是均匀分布时, 相应的Hausdorff距离往往是在给定的阈值之内的.
21.5 Angles
针对角度进行重新网格化的代表论文是Isotropic Surface Remeshing without Large and Small Angles.此处的小角度或者大角度是指在给定的区间$[\beta_{\min}, \beta_{\max}]$之外的角度. 论文算法的核心思想是:
$\cdot$ 去除大角度: Edge Splitting.
$\cdot$ 提升小角度: Edge Collapsing.
如下图所示, 1) Split; 2) Flip.
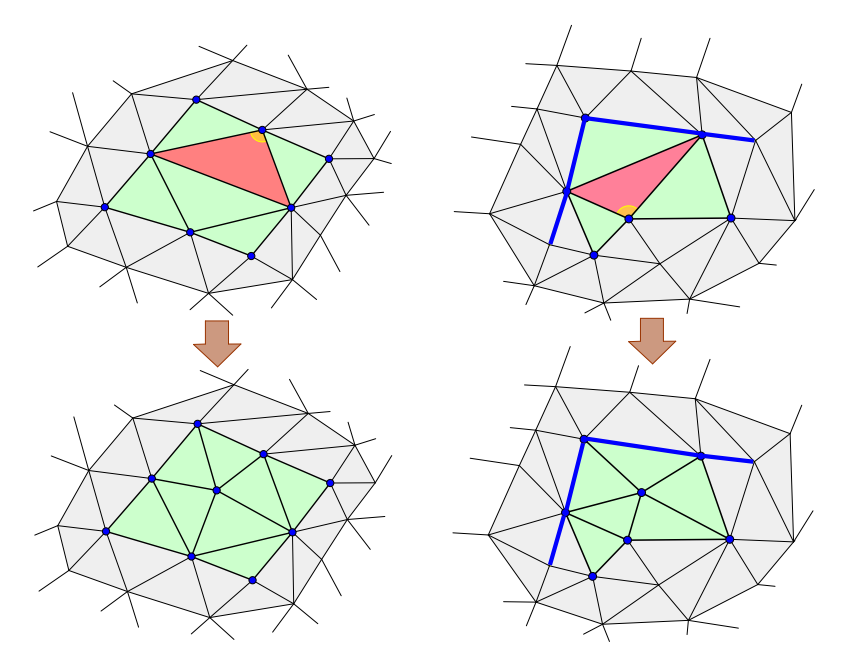
P22: Delaunay Triangulations
这节课介绍的内容还是很有意思的, 主要侧重于Delaunay三角剖分中一些性质的证明. 自己虽然之前用过, 但并没有深入地了解过相关性质的证明~
22.1 Convex Hull
$\cdot$ 凸集. 对于集合$P \in R^d$内的任意两点$p,q$, 若之间的连线$\overline{pq} \in P$, 则称集合$P$为一个凸集. 也可以利用连通性作一个等价的定义: 对于任意直线$l \in R^d$与集合$P \in R^d$, 若$l \cap P$均为一个连通集, 则称集合$P$为一个凸集. 对于任意凸集的集合族$\{ P_i \}$, $\cap_i P_i$均为凸集.
$\cdot$ 凸包. 有限点集$P \in R^d$的凸包构成一个凸多面体, 记为$conv(P)$. 若$p \in P$且$p \notin conv(P \backslash \{ p \})$, 则称$p$为$conv(P)$的一个顶点(或Extremal Point). 求解凸包的算法主要有两种.
$\quad \cdot$ Carathéodory’s Theorem. 遍历$P$中每个点$p$, 判断是否存在$q,r,s \in P \backslash \{ p \}$, 使得$p$在$q,r,s$构成的三角形内部. 若不存在符合条件的三个点, 则当前点$p$是$P$的凸包的一个顶点. 该算法的时间复杂度为$O(n^4)$.
$\quad \cdot$ Carathéodory’s Theorem. 遍历$P$中每个点$p$, 判断是否存在$q,r,s \in P \backslash \{ p \}$, 使得$p$在$q,r,s$构成的三角形内部. 若不存在符合条件的三个点, 则当前点$p$是$P$的凸包的一个顶点. 该算法的时间复杂度为$O(n^4)$.
$\quad \cdot$ The Separation Theorem. 遍历$P^2$中的点对$(p,q)$, 判断$P \backslash \{ p, q\}$中的所有点是否都在$p, q$之间的连线$\overline{pq}$的一侧, 若是则说明$\overline{pq}$是$P$的凸包边界的一部分. 该算法的时间复杂度为$O(n^3)$.
22.2 Triangulation
三角剖分是把指由一个多边形剖分得到的三角形集合, 其应用是十分广泛的, 如面积计算, 插值等. 在一个有限点集$P \subset R^2$上的三角剖分是一个三角形集$\mathcal{T}$, 并满足如下约束:
$\cdot$ $conv(P) = \cup_{T \in \mathcal{T}} T$.
$\cdot$ $P = \cup_{T \in \mathcal{T}} V(T)$.
$\cdot$ 对于任意集合对$T, U \in \mathcal{T}$, $T \cap U$要么仅含公共点, 要么仅含公共边, 要么是空集.
22.3 Delaunay Triangulation
二维Delaunay三角剖分 给定平面上的离散点集$P$, 若存在一个三角剖分$DT(P)$, 使得$DT(P)$内的任意一个三角形的外接圆内部都不含$P$中的元素(空圆特性, 也可以利用内接四边形的对角互补的性质辅助判断是否满足空圆特性), 则称三角剖分$DT(P)$为一个二维Delaunay三角剖分. 以下均只讨论二维情形, 故将二维Delaunay三角剖分简记为Delaunay三角剖分. Delaunay三角剖分的存在性与唯一性均是无法保证的.
The Lawson Flip Algorithm是一种生成Delaunay三角剖分的经典算法. 其算法步骤为:
1) 计算离散点集$P$的一个三角剖分.
2) 遍历三角剖分中的每一个四边形, 若当前四边形对应的子三角剖分不是一个Delaunay三角剖分, 则对四边形内的边执行Flip操作.
该算法的理论保证是如下定理:
设$P \subseteq R^2$是$n$个点的集合, $\mathcal{T}$是$P$的一个三角剖分. 则Lawson Flip算法最多执行$\binom{n}{2} = O(n^2)$次Flip操作, 且最终得到的三角剖分$D$是$P$的一个Delaunay三角剖分.
以下仅进行直观意义上的证明, 分为两步进行.
1) 算法必定能够停止.
2) 算法最终得到的三角剖分是一个Delaunay三角剖分.
证明前需要先引入The Lifting Map的概念: 给定点$p = (x, y) \in R^2$, 其提升$l(p)$为点$l(p) = (x, y, x^2 + y^2) \in R^3$. 从几何上来看, $l$将点竖直提升到一个单位抛物面上, 如下图所示.
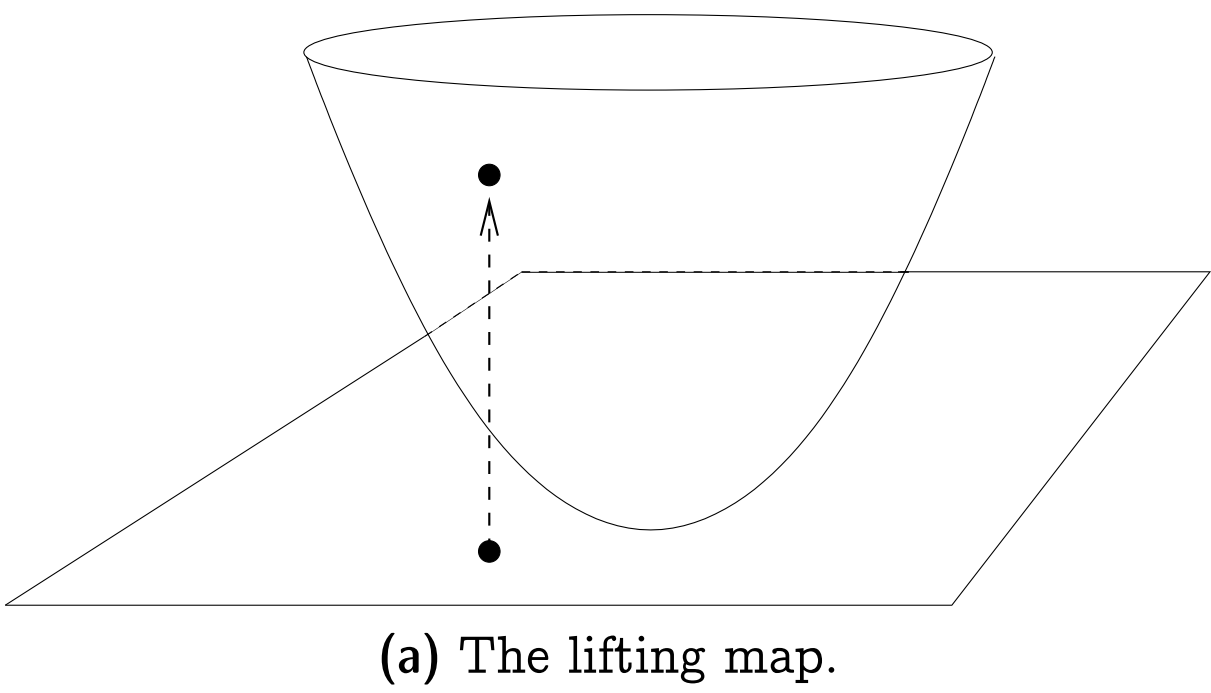
关于Lifting Map的一个重要引理为: 设$C$是平面上的一个圆, 经提升后$l(C) = \{ l(p) | p \in C \}$位于一个唯一的平面$h(C) \subset R^3$上. 此外, 任一点$p \in R^2$在圆$C$内(外) 当且仅当点$p$经提升后得到的点$l(p)$在平面$h(C)$下(上), 如下图所示.
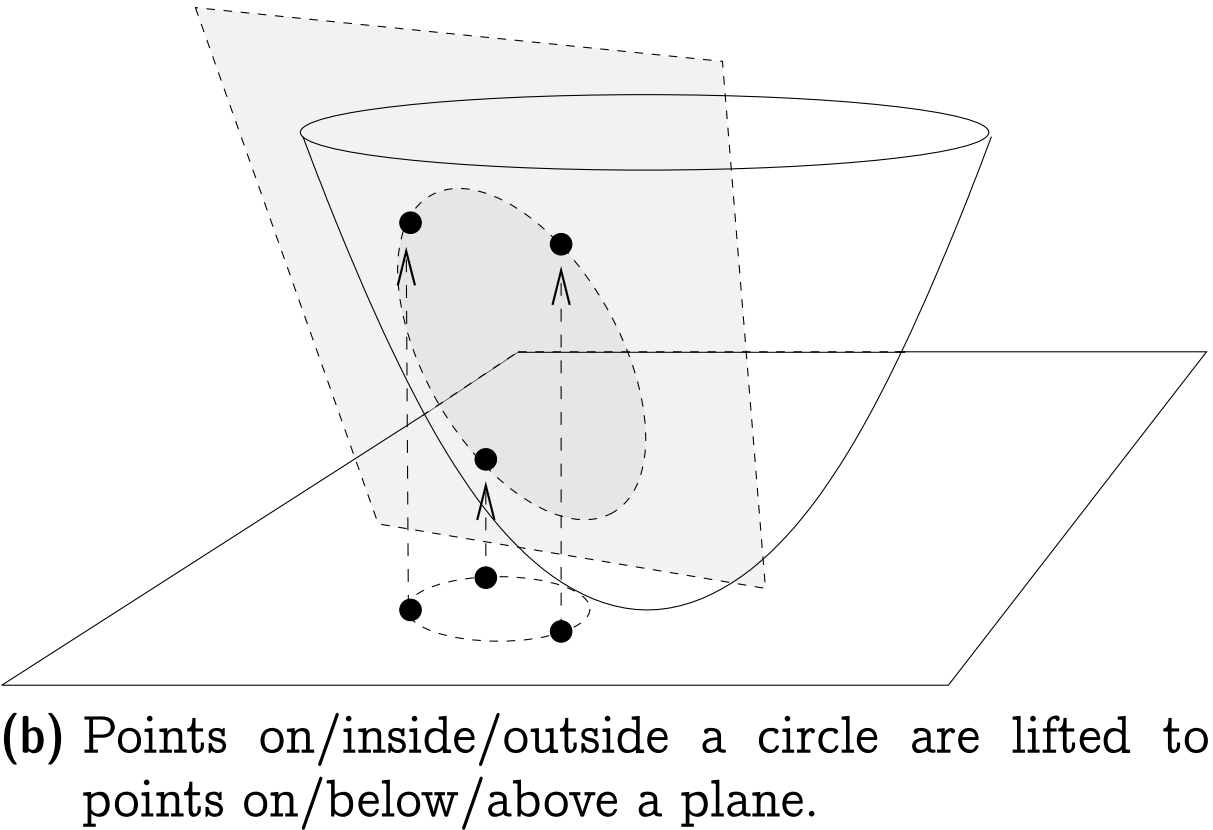
简单证明一下这个引理: 不妨设平面上的圆$C$对应的方程为$$(x – x_C)^2 + (y – y_C)^2 = r_C^2,$$其中$(x_C, y_C)$为圆$C$的圆心, $r_C$为圆$C$的半径. 对于圆周上的点$(x, y)$, 由于点$(x, y)$经提升后位于抛物面上, 满足关系式$z = x^2 + y^2$, 代入圆$C$对应的方程可得$$z = 2x_Cx + 2y_Cy + (r^2 – x_C^2 – y_C^2),$$显然这是一个平面方程, 且由于圆$C$的圆心$(x_C, y_C)$与半径$r_C$均是固定的, 故该平面方程也是唯一的. 类似可推得引理剩余部分.
$\cdot$ Termination. 从几何上看, Lawson Flip算法可以解释为将一个四面体中最上面的两个三角形替换为最下面的两个三角形的操作, 可结合上述引理与下图理解.
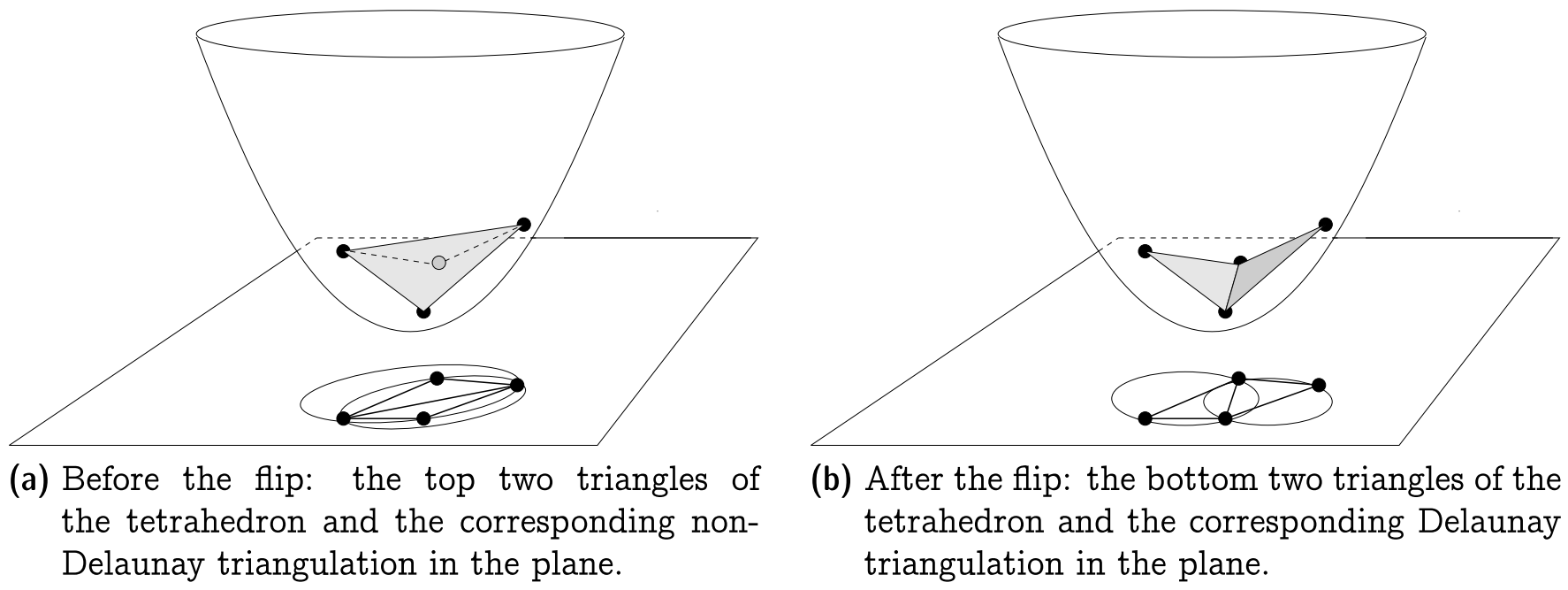
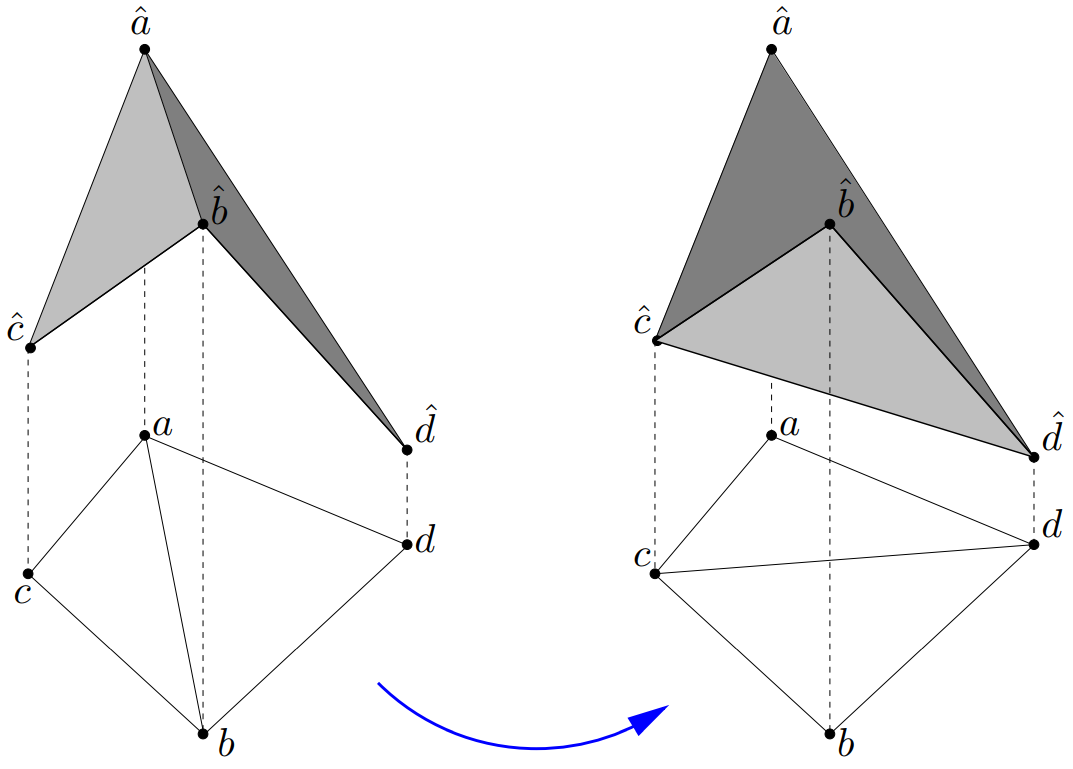
从四面体体积的角度来看, 每一次进行Lawson Flip算法都减少了相应的四面体体积(其实这里我没有很理解囧), 由于四面体的体积总是有下界的(0是其下界), 而每次进行Lawson Flip算法得到的四面体的体积构成的序列是一个单调递减序列, 故由单调有界定理可知该算法是可收敛的. 另外一方面, 一旦某条边被翻转, 则该边所在的平面会严格处于抛物面之上, 且不会再被翻转(其实这里我也没有很理解囧). 又$n$个点最多产生$\binom{n}{2}$条边, 故Lawson Flip算法执行的次数总是有上界的.
$\cdot$ Correctness. 首先定义局部Delaunay(Locally Delaunay) 剖分: 设由Lawson Flip算法得到三角剖分$D$, $\triangle, \triangle’$是$D$中的两个相邻三角形. 若$\triangle$的外接圆内部不含$\triangle’$的任一顶点, 且反过来也成立, 则称$\triangle, \triangle’$构成一个局部Delaynay剖分. 接下来从直观意义上简单证明一下由Lawson Flip算法得到的局部Delaynay剖分可以得到全局Delaynay剖分的事实.
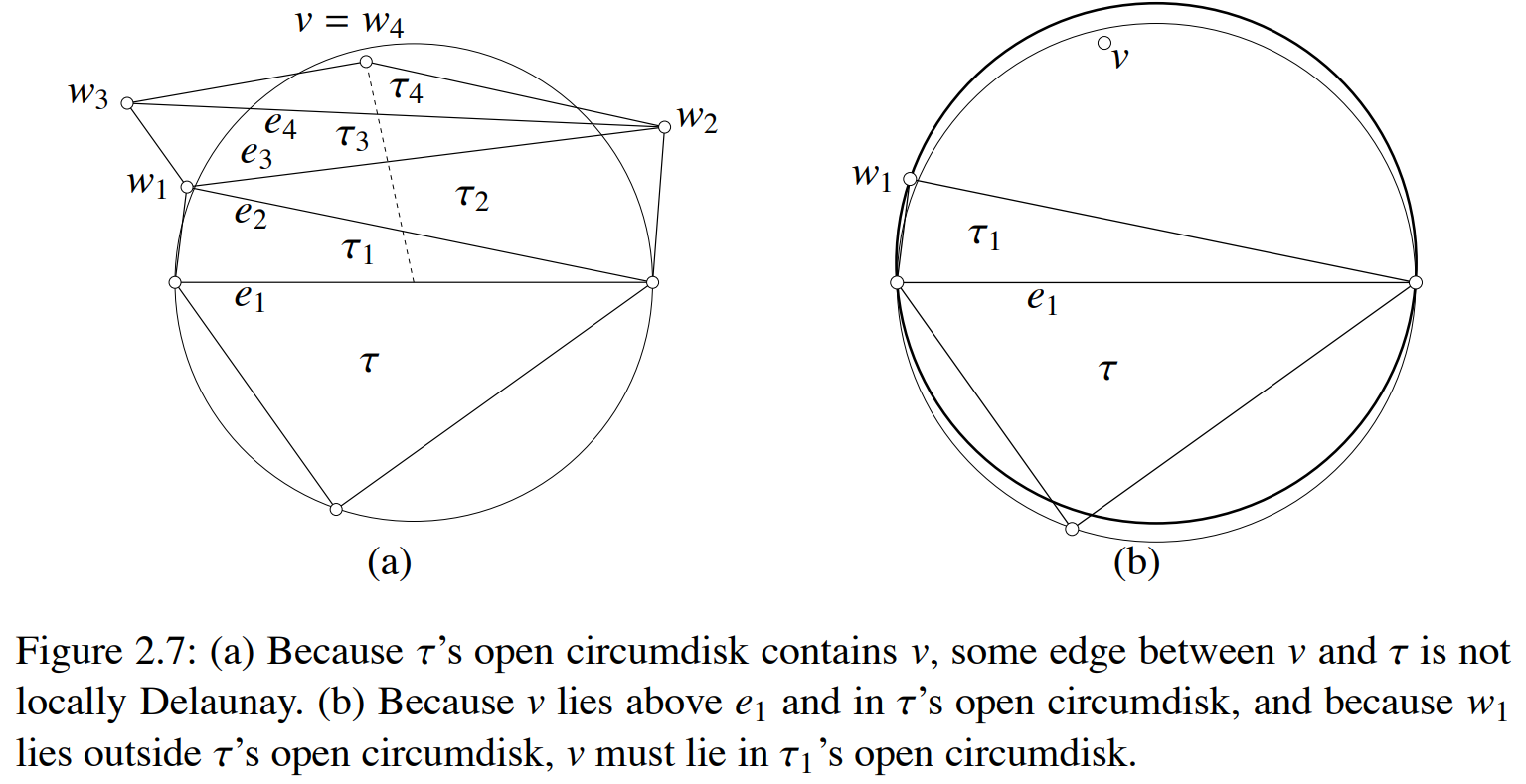
证: 采用反证法, 若局部Delaunay三角剖分$D$并非全局Delaynay剖分, 则设$\tau$是局部Delaunay三角剖分$D$中的一个三角形, $w_n \in P$是落在$\tau$的外接圆外部的一个点, $\tau_n$是局部Delaunay三角剖分$D$中以$w_n$为顶点的一个三角形, 则可以将$v$与$\tau$中任一点相连得到线段$l$, 沿着线段$l$可得到一列局部Delaunay三角剖分$D$中按顺序相邻的三角形$\tau, \tau_1, \cdots, \tau_n$.
由于三角形$\tau, \tau_1$相邻, 由局部Delaunay三角剖分定义可知, $\tau_1$中与公共边相对的顶点$w_1$必定落在$\tau$的外接圆外部. 再看相邻的两个三角形$\tau_1, \tau_2$, 由局部Delaunay三角剖分定义可知, $\tau_2$中与公共边相对的顶点$w_2$必定落在$\tau_1$的外接圆外部, 从而落在$\tau$的外接圆外部, 如上图(b)中所示…… 类似可推得, $\tau_n$中的顶点$w_n$也必落在$\tau$的外接圆外部, 而这与假设矛盾, 故命题得证.
22.4 Maximize the Minimum Angle
若离散点集$P$的Delaunay三角剖分存在, 则其最小角是离散点集$P$的所有三角化的最小角的最大值. 接下来简单证明Delaunay三角剖分能够最大化最小角的特性.
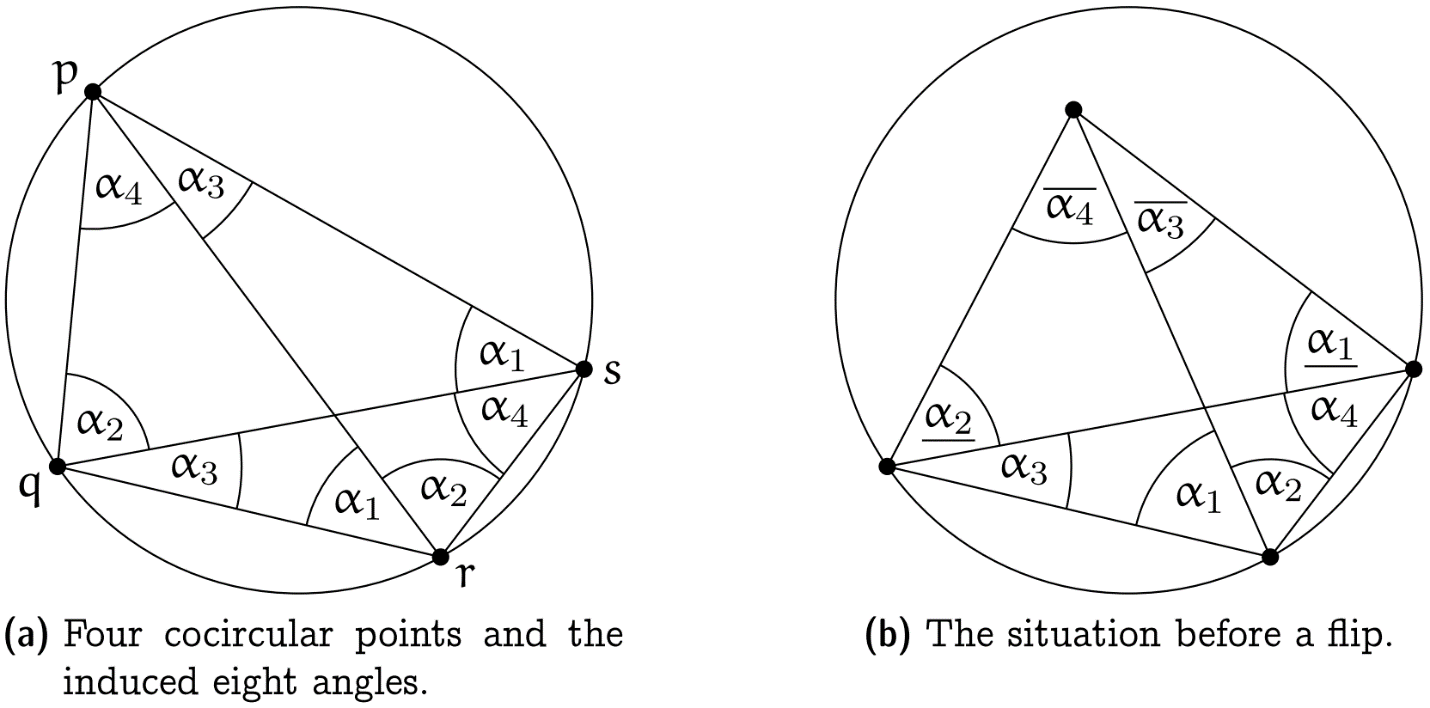
证: 仅关注上图(b)即可,
$\cdot$ Flip前两个三角形的六个内角分别为$\alpha_1 + \alpha_2, \alpha_3, \alpha_4, \underline{\alpha_1}, \underline{\alpha_2}, \overline{\alpha_3} + \overline{\alpha_4}$.
$\cdot$ Flip后两个三角形的六个内角分别为$\alpha_1, \alpha_2, \overline{\alpha_3}, \overline{\alpha_4}, \underline{\alpha_1} + \alpha_4, \underline{\alpha_2} + \alpha_3.$
由圆周角定理易推得$$\alpha_1 > \underline{\alpha_1}, \alpha_2 > \underline{\alpha_2}, \overline{\alpha_3} > \alpha_3, \overline{\alpha_4} > \alpha_4,\\\underline{\alpha_1} + \alpha_4 > \alpha_4, \underline{\alpha_2} + \alpha_3 > \alpha_3,$$从而命题得证.
P23: Optimal Delaunay Triangulation与Voronoi Diagram
本节是该系列课程的最后一节, 看着Voronoi Diagram与CVT再次出现在眼前, 真的挺有亲切感的~
23.1 Optimal Delaunay Triangulation
有时候若仅是对离散点集作Delaunay三角剖分, 是无法得到高质量的三角剖分的, 如存在最小角依旧较小的问题. 为了尽可能地实现最小角最大化的目标, 还应适当调整点的位置, 一般从曲面逼近的角度出发来优化下述能量函数,$$E = \sum_{T \in \mathcal{T}} \int\limits_{T} | \hat{u}(x) – u(x) | dx,$$其中, 各符号说明如下:
$\cdot$ $u(x): z = x^2 + y^2.$
$\cdot$ $\hat{u}(x):$ $u$的分片线性插值.
$\cdot$ $\mathcal{T}:$ 一个三角剖分.
从直观意义上理解, 更高质量的三角剖分对应的四面体体积之和也往往更小. $u(x), \hat{u}(x)$也分别对应下图中的抛物面与三角面.

容易注意到, 能量函数$E$含有两组未知变量, 分别是顶点位置集与三角剖分.针对这种含两组未知变量的能量函数, 可采用交替迭代的方式.
$\cdot$ 更新三角剖分. 遍历所有边, 对不满足空圆特性的边执行Flip操作.
$\cdot$ 更新顶点位置.
主要关注一下顶点位置的更新. 假设此时Delaunay三角剖分已被固定, 则$$E = \sum_{T \in \mathcal{T}} \int\limits_{T} | \hat{u}(x) – u(x) | dx = \sum_{T \in \mathcal{T}} \int\limits_{T} \hat{u}(x) dx + C\\=\sum_{T \in \mathcal{T}}\frac{|T|}{3}(u(p_i) + u(p_j) + u(p_k)) + C,$$其中, 上述推导中第二个等式是根据Delaunay三角剖分的性质得到的, 此时$\hat{u}(x)$在各个三角形$T$上总是大于$u(x)$的, 故可去除绝对值符号; 第三个等式则是由三棱柱的体积公式得到. 接下来令其梯度为0, 得$$\nabla E_{p_i} = \sum_{T \in \Omega(i)} \frac{\nabla|T|}{3}(u(p_i) + u(p_j) + u(p_k)) + \frac{|\Omega|}{3}\nabla u(p_i) = 0\\ \because \sum_{T \in \Omega(i)} \frac{\nabla|T|}{3}u(p_i) = \frac{u(p_i)}{3} \sum_{T \in \Omega(i)} \nabla|T| \\= \frac{u(p_i)}{3} \nabla|\Omega| = \frac{u(p_i)}{3} \cdot 0 = 0\\ \therefore \nabla u(p_i) = -\frac{1}{|\Omega|} \sum_{T \in \Omega(i)} \frac{\nabla|T|}{3}(u(p_j) + u(p_k)).$$接下来便可利用Gauss–Seidel迭代, 逐步根据每一个$u(p_i)$的梯度更新每一个点$p_i$的位置(由于发现老师在推导时出现错误, 故此处也不再继续推导, 后面若有需要再补充). 此外, 此处$u(x)$也并不局限于前面提到的Lifting Map.
23.2 二维Voronoi Diagram
$\cdot$ 邮局问题. 二维Voronoi Diagram(以下均只讨论二维情形, 故将二维Voronoi Diagram简记为Voronoi Diagram) 起源于邮局问题: 假设一个城市有$n$个邮局$p_1, \cdots, p_n$, 有人处于该城市的点$q$处, 想知道哪个邮局离他最近? 显然, 一个最简单的方法便是遍历所有邮局, 计算最短距离. 但一个更彻底的解决方案应该是建立一个数据结构来应对各种各样的查询与邮局数量增加带来的遍历消耗. 于是, 可以将该平面剖分为若干个区域, 每个区域内都有且只有一个种子点(对应于一个邮局的位置点), 使得每个区域内的所有点距离当前区域内的种子点的距离相比较距离其它种子点的距离是最近的. 接下来便可以给出Voronoi Cell的数学定义.
$\cdot$ Voronoi Cell 给定$R^2$上的点集$P = \{ p_1, \cdots, p_n \}$, $p_i \in P$所属的Voronoi Cell $VP(i)$定义为$$VP(i) := \{ q \in R^2 | \| q – q_i \| \le \| q – p \|, \forall p \in P \},$$同时每一个Voronoi Cell $VP(i)$需要满足下述约束.
$\quad \cdot$ $VP(i) = \cap_{j \ne i} H(p_i, p_j)$, 其中$H(p_i, p_j)$为$p_i, p_j$之间的Bisector.
$\quad \cdot$ $VP(i)$非空且为凸集.
$\quad \cdot$ 平面上每一点都只属于一个Voronoi Cell, 故所有的Voronoi Cell构成平面的剖分.
接下来介绍Voronoi Diagram的相关引理, 记$VV(P)$为Voronoi Diagram的顶点集, $VE(P)$为Voronoi Diagram所有边构成的集合, $VR(P)$为Voronoi Diagram所有面构成的集合.
$\cdot$ 引理1 对于$\forall v \in VV(P)$, 下列命题成立.
$\quad \cdot$ $v$为$VE(P)$中至少三条边的交集中的元素.
$\quad \cdot$ $v$为$VR(P)$中至少三个面的交集中的元素.
证: 由于所有的Voronoi Cell均为凸集, 故每一个内角均小于$\pi$. 显然, 若$v$为$VE(P)$中不多于两条边的交集中的元素, 则$v$周围的内角和小于$2\pi$, 从而所有的Voronoi Cell无法构成平面的剖分, 矛盾. 故命题得证.
$\cdot$ 引理2 对于$\forall v \in VV(P)$, 下列命题成立.
$\quad \cdot$ $v$为某个圆$C$的圆心, 其中, 圆$C$至少过$P$中三个点.
$\quad \cdot$ $C(v)^{\circ} \cap P = \emptyset$, 其中, $C(v)^{\circ}$为$C(v)$的内点集.
证: 反证法, 假设存在点$p_l \in C(v)^{\circ}$, 则顶点$v$距离$p_l$最近(相比较$p_1, \cdots, p_k$), 这与顶点$v$处于$VP(1),VP(2), \cdots$或者$VP(k)$内的事实矛盾, 故命题得证.
23.3 Duality: Delaunay triangulation
对于给定的图$G$, 得到图$G$的对偶图$G’$的规则如下:
$\cdot$ 在图$G$的每一个面$f_i$内取一个点$v_i’$作为对偶图$G’$的一个顶点.
$\cdot$ 对于图$G$的一条边$e_i$, 若$e_i$为图$G$中两个面的公共边, 则连接这两个面的顶点, 且其连线需要穿过$e_i$; 若$e_i$为图$G$中某个面的割边, 则以该面顶点作环, 且让它与$e_i$相交.
定理 设点集$P \subset R^2$含有的点的数量大于3, 且点集$P$内任意三点不共线, 任意四点不共圆, 则点集$P$的Voronoi Diagram $VD(P)$的平面对偶图是唯一的, 且恰为点集$P$的Delaunay三角剖分.
证: (必要性) 根据凸包, 三角剖分与空圆特性的定义即可得证.
(充分性) 根据外接圆圆心与空圆特性的定义即可得证.
23.4 CVT
CVT是一种特殊的Voronoi Diagram, 其每一个Voronoi Cell $V_i$的种子点$p_i$都恰为其质心, 其中, Voronoi Cell $V_i$的质心定义为$$c_i = \frac{\int_{V_i} \| x – p_i \|^2 dx}{\int_{V_i}dx}.$$通常可通过优化下述能量函数得到CVT:$$E(p_1, \cdots, p_n, V_1, \cdots, V_n) = \sum^n_{i = 1} \int_{V_i} \| x – p_i \|^2 dx.$$对于上述含有两组未知变量的最优化问题而言, 可利用Lloyd迭代算法进行求解, 算法步骤如下所示.
$\cdot$ 根据种子点$p_i$构造相应的Voroni Diagram.
$\cdot$ 计算Voroni Cell $V_i$的质心$c_i$, 并移动种子点$p_i$至相应的质心处.
$\cdot$ 重复上述两步直至算法收敛.
23.5 Variational Shape Approximation(VSA)
之前已经学过VSA, 如今学完了CVT, 我们可以重新从CVT的角度出发解释VSA. 回顾一下, VSA的目标是用一个代理集$P = \{ P_1, \cdots, P_k \}$逼近输入网格$M$, 即$$M = R_1 \cup \cdots \cup R_k \approx P_1 \cup \cdots \cup P_k$$ 其中, $R = \{ R_1, \cdots, R_k \}$是对输入网格$M$的一个剖分, 代理$P_i$是指空间中的一个平面$(x_i, n_i)$. 而VSA所研究的最优化问题为: 给定$k \in N$, 三角网格$M$与误差度量$E$($L^2$或$L^{2,1}$), 寻找一个剖分$R = \{ R_1, \cdots, R_k \}$与一个代理集$P = \{ P_1, \cdots, P_k \}$使得下述关于扭曲程度的能量函数最小,$$E(R, P) = \sum^k_{i=1}E(R_i, P_i),$$其中, $R_i$与$P_i$之间的误差度量有两种定义方式, 分别为
$\cdot$ $L^2$误差:$$L^2(R_i, P_i) = \int_{x \in R_i}(n^T_ix – n^T_ix_i)^2dx.$$$\cdot$ $L^{2,1}$误差:$$L^{2,1}(R_i, P_i) = \int_{x \in R_i}\left \| n(x) – n_i \right \|^2 dx.$$可使用Lloyd算法求解上述最优化问题, 算法步骤如下所示.
$\cdot$ 初始化. 任选$k$个三角形构成的集合作为$R$, 这$k$个三角形所在的平面构成的集合作为$P$.
$\cdot$ 几何划分阶段. 寻找对$P$拟合效果最好的剖分$R$.
$\cdot$ 代理拟合阶段. 固定剖分$R$, 同时调整代理集. 与上一节介绍的Lloyd算法步骤有所不同的是, 此处需要计算的”质心”是$n_i$.
算法伪代码如下图所示.

至此, 数字几何处理课程笔记完结撒花. *★,°*:.☆( ̄▽ ̄)/$:*.°★* 。