春节在家的时间仅剩大约三天了, 时间过得真快, 假期前几天其实并没有怎么看代数拓扑的东西(回家路上看了一些Seifert & Van Kampen定理相关的内容), 这两天主要补充一下Seifert & Van Kampen定理相关内容的学习, 并以此文作为记录.
参考材料
1. 如何理解 Van-Kampen 定理?
2. 什么是群胚(groupoid)?
3. 群胚
1. Seifert & Van Kampen定理
设$X, Y$都是$Z$的开子集, $Z = X \cup Y$, $X \cap Y$非空并且道路连通. 设$i: X \cap Y $$ \mapsto X$, $j: X \cap Y \mapsto Y$, $p : X \mapsto X \cup Y$, $q : Y \mapsto $$ X \cup Y$是相应的含入映射.
$\\$ 在$X \cap Y$中取定基点$x_0$, 并设$\pi_1(X, x_0)$具有表出$\left \langle C \ | \ R \right \rangle$, $\pi_1(Y, $$ x_0)$具有表出$\left \langle D \ | \ S \right \rangle$, 而交集的基本群$\pi_1(X \cap Y, x_0)$具有表出$\left \langle E \ | \ T \right \rangle$. 对于每个生成元$e \in $$ E$, 取定一个以$C$为字符集的字$e_C$, 使得在$\pi_1(X, x_0)$按$e_C$计算得$i_\pi(e)$, 再取定一个以$D$为字符集的字$e_D$, 使得在$\pi_1(Y, x_0)$中按$e_D$计算得$j_\pi(e)$. 则$\pi_1( $$ X \cup Y, x_0)$具有表出$$\left \langle C_{p_\pi} \cup D_{q_\pi} \ | \ R_{p_\pi} \cup S_{q_\pi} \cup \widetilde{E} \right \rangle,$$其中$\widetilde{E} = \{ p_\pi(e_C)^{-1}q_\pi(e_D) \ | \ e \in E \}$. 或者等价地讲,$$\pi_1(X \cup Y, x_0) \cong (\pi_1(X, x_0) * \pi_1(Y, x_0))/N \\ := \pi_1(X, x_0) *_{N} \pi_1(Y, x_0),$$其中, 论述”在$\pi_1(X, x_0)$按$e_C$计算得$i_\pi(e)$”是指若字符集$C$生成的自由群$F(C)$到字符集$C$生成的自由群$\pi_1(X, x_0)$之间的映射为$\xi$, 则$\xi(e_C) = i_\pi(e)$; $N$是自由积中包含所有形如$i_\pi(e)^{-1}j_\pi(e)$的字(这里$e \in \pi_1(X \cap Y, x_0)$) 的最小正规子群, 即$$N = [\{ i_\pi(e)^{-1}j_\pi(e) \ | \ e \in \pi_1(X \cap Y, x_0) \}],$$之所以要模去这个正规子群, 是因为$p_\pi(e_C)^{-1}q_\pi(e_D)$在一条道路的字$w$中是多余的, 此时$p_\pi$与$q_\pi$作用的对象$e_C$(或$e_D$) 本质上是一致的, 均为$X \cap Y$中的的闭道路类$e$.
$\\$ 定理内容比较长, 但背后的思想还是比较简单的. 定理是指若要计算一个拓扑空间的基本群, 可以把它拆成两个有连通交集的连通开集的并, 则其基本群是由两个开集的基本群, 其交集的基本群以及交集到开集、开集到空间的嵌入映射所完全决定的; 具体来说, 即开集的基本群给出生成元, 而交集的基本群则给出生成关系. 在交集不连通的情况下也有表述更复杂的版本, 同时还有其它一些变体.
$\\$ 我们可以类比集合并集元素数量的计算公式:$$|A \cup B| = |A| + |B| – |A \cap B|.$$也可以类比线性空间并集维数的计算公式:$$dim(A + B) = dim(A) + dim(B) – dim(A \cap B).$$上述两个例子都很直观, 集合$A, B$放在一起后, 那么在最后的结果中, 集合$A, B$都作出Contribute, 但是有一部分$A, B$被视为等同地位了(也就是交集), 从而这一部分的$A, B$分别作出的Contribute也被视为等同地位. 这也就是为什么要减去交集的原因. 更直观的理解角度是看集合里的元素, 或者线性空间的基, 均包含三部分, 只在集合$A$里的, 只在集合$B$里的, 以及被视为等同地位的那部分(即在交集里的). 在某种程度上, 当把两个线性空间放在一起后, 就自然给出了一个短正合序列. 上述两个例子都告诉我们, 集合的基数与线性空间的维度都满足短正合序列中间项的性质, 而Van Kampen定理告诉我们基本群也是同理亦然.
2. Seifert & Van Kampen定理群胚版本
Seifert & Van Kampen定理也有使用基本群胚语言描述的版本, 先介绍群胚的定义. 一个群胚是指一个范畴$\mathcal{C}$, 其中每个态射都是可逆的: 对任意$X, Y \in \mathcal{C}$及$f \in \mathcal{C}(X, Y)$, 存在唯一的$f^{-1} \in \mathcal{C}(Y, X)$, 使得$$f^{-1} \circ f = 1_X, f \circ f^{-1} = 1_Y.$$对范畴$\mathcal{C}$, 它的群胚化$\mathcal{C}^{\simeq}$是如下定义的群胚:
$\\$ $\cdot$ 对象: 与$\mathcal{C}$中相同.
$\\$ $\cdot$ 态射: $\mathcal{C}$中所有可逆态射.
$\\$ 群可以看成是只有一个对象的群胚. 换言之, 群胚是群的胚化: 对于任意群$G$, 定义群胚(记为$G^{\simeq}$) 如下:
$\\$ $\cdot$ $\mathcal{O}b(G^{\simeq}) = \{ pt \}$为一个单点集.
$\\$ $\cdot$ $Mor(G^{\simeq}) = \{ g \in G\}$, 此处亦可理解为群中每一个元素$g$均诱导了一个唯一的态射$g^{\simeq}$.
$\\$ $\cdot$ 态射的复合规则为$g^{\simeq} \circ h^{\simeq} := h \cdot g$.
$\\$ 这样一来, 群的乘法运算的结合律保证了态射的复合运算的结合律, 群的单位元保证了恒等态射的存在性, 这两点说明$G^{\simeq}$是一个范畴; 而群中每个元素都有逆元的事实则保证了每个态射均为同构映射的事实, 从而说明$G^{\simeq}$为一个群胚.
$\\$ 再来看看基本群胚$\pi_1(X)$, $\pi_1(X)$亦为一个范畴, 对象是$X$中所有的点, 态射是连结两点的所有连续路径的同伦类, 单位元为常路径, 复合运算为路径的串接. 给定任意$x \in X$, 由它张成的满子范畴就是基本群$\pi_1(X, x)$. 从朴素的观点来看, 基本群胚含有的信息相当于一族基本群$\{ \pi_1(X, x) | [x] \in \pi_0 $$ (X) \}$, 即对$X$的每个连通分支(路径) 各选一个点, 并各自取这些点上的基本群. 这背后的原因是, 若两点$x, y$处于同一个连通分支(路径), 那么$\pi_1(X, x)$(非典范) 同构于$\pi_1(X, $$ y)$, 这个同构取决于连结$x, y$的路径(的同伦类), 即存在一个如下定义的同构映射$r_*$,$$r_* : \pi_1(X, x) \to \pi_1(X, y),\\\left \langle \alpha \right \rangle \mapsto \left \langle r^{-1} \alpha r \right \rangle.$$在介绍完群胚的定义以后, 我们便可以用群胚的语言来描述Seifert & Van Kampen定理: 设$X$为一个拓扑空间, $X_0, X_1 \subset X$, $X_{01} = $$ X_0 \cap X_1$, $int( $$ X_0) \cup int(X_1) = X$, 我们有如下两个图表, 其中图表(#)为一个Cocartesian图表.
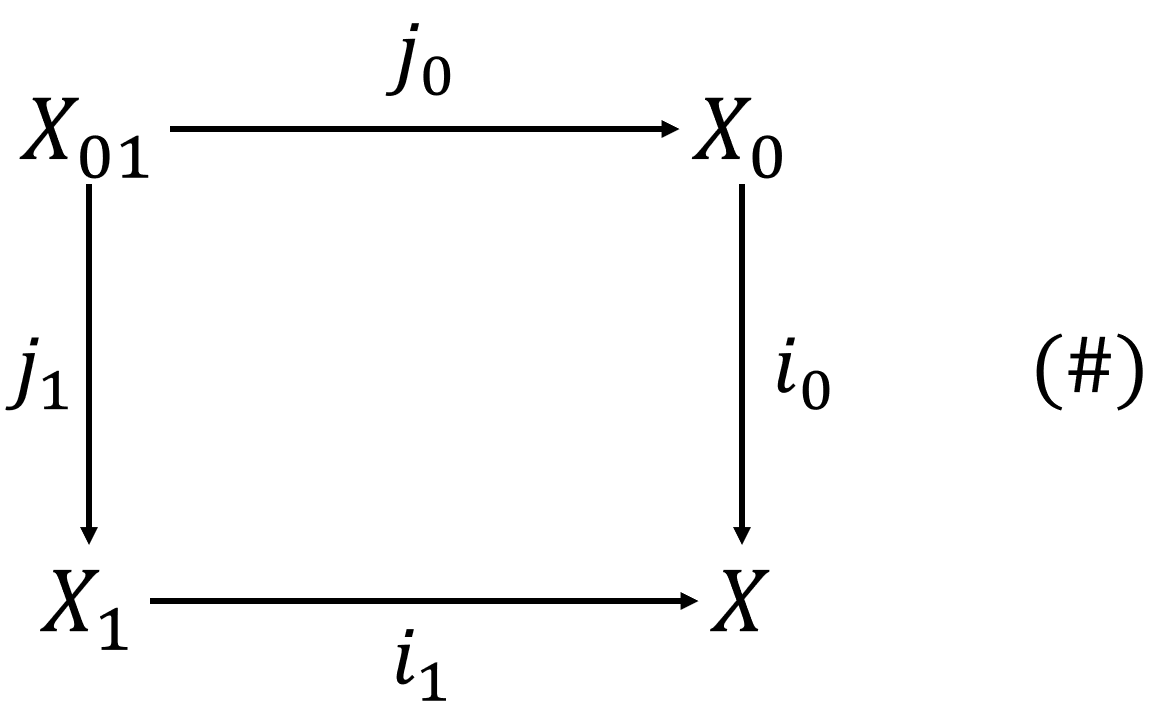
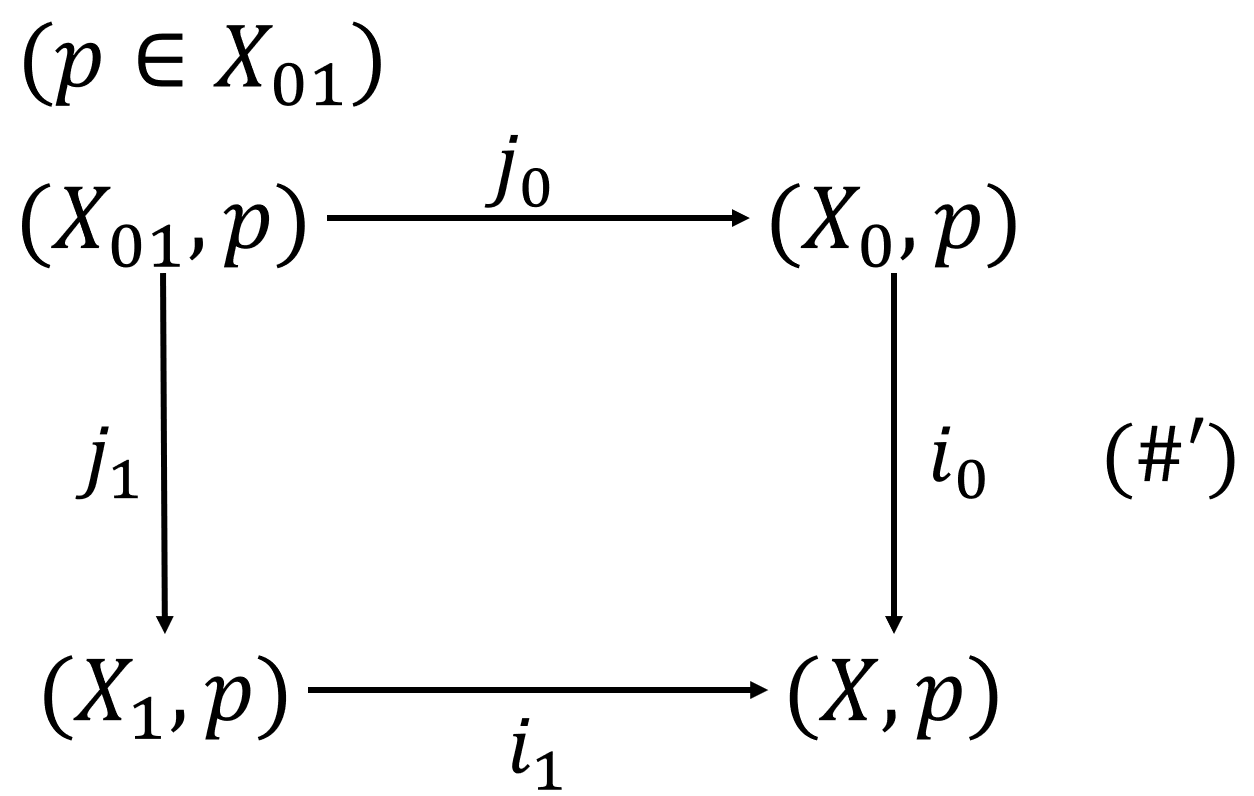
进一步假设: $p \in X_{01}$, $X_0, X_1, X_{01}$均道路连通, 则将带点的拓扑空间映射到群胚的函子$\pi_1$将图表(#’)变为群胚中的Cocartesian图表, 如下图所示.
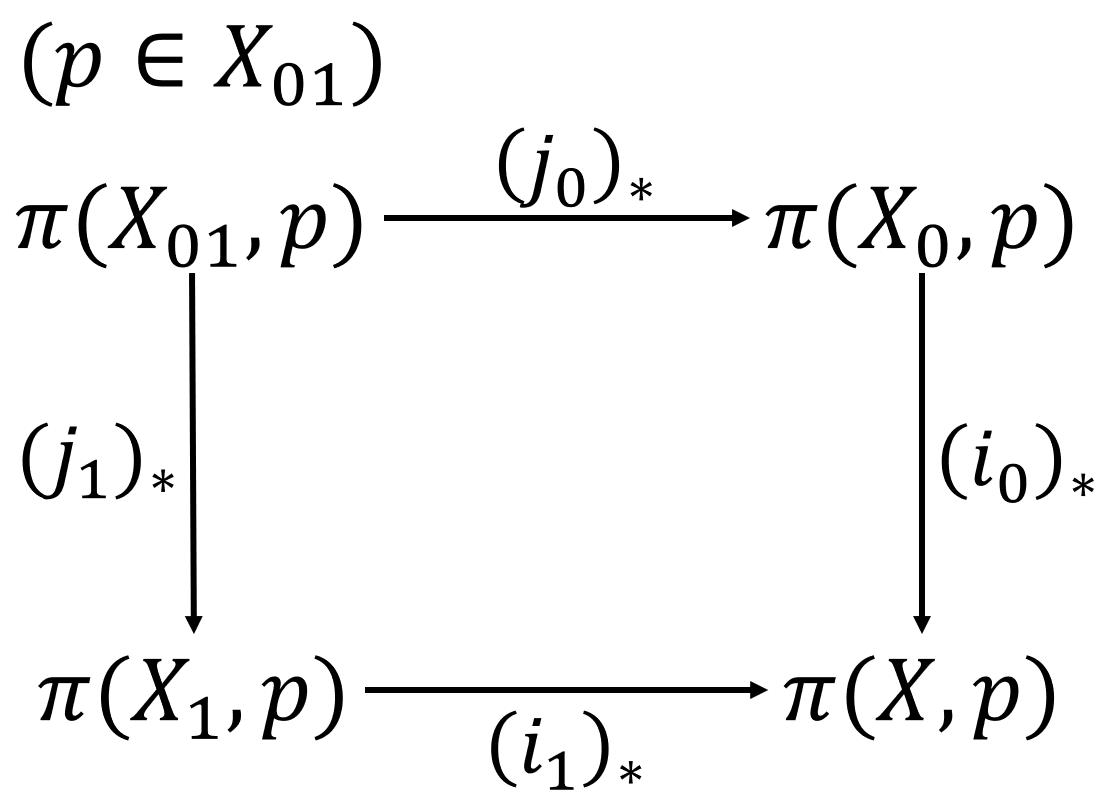
推论 $\pi_1(X, p) \cong \pi_1(X_0, p) *_{\pi_1(X_{01}, p)} \pi_1(X_1, p)$.
Seifert & Van Kampen定理更一般的形式又被称为R. Brown定理: 设$X$为一个拓扑空间, $X_0, X_1 \subset X$, $X_{01} = X_0 \cap X_1$, $int(X_0) \cup $$ int(X_1) = X$(注意无需假设$X_0, X_1, X_{01}$均道路连通), 则将拓扑空间映射到群胚的函子$\prod$把Cocartesian图表(#)变为群胚中的Cocartesian图表, 如下图所示.
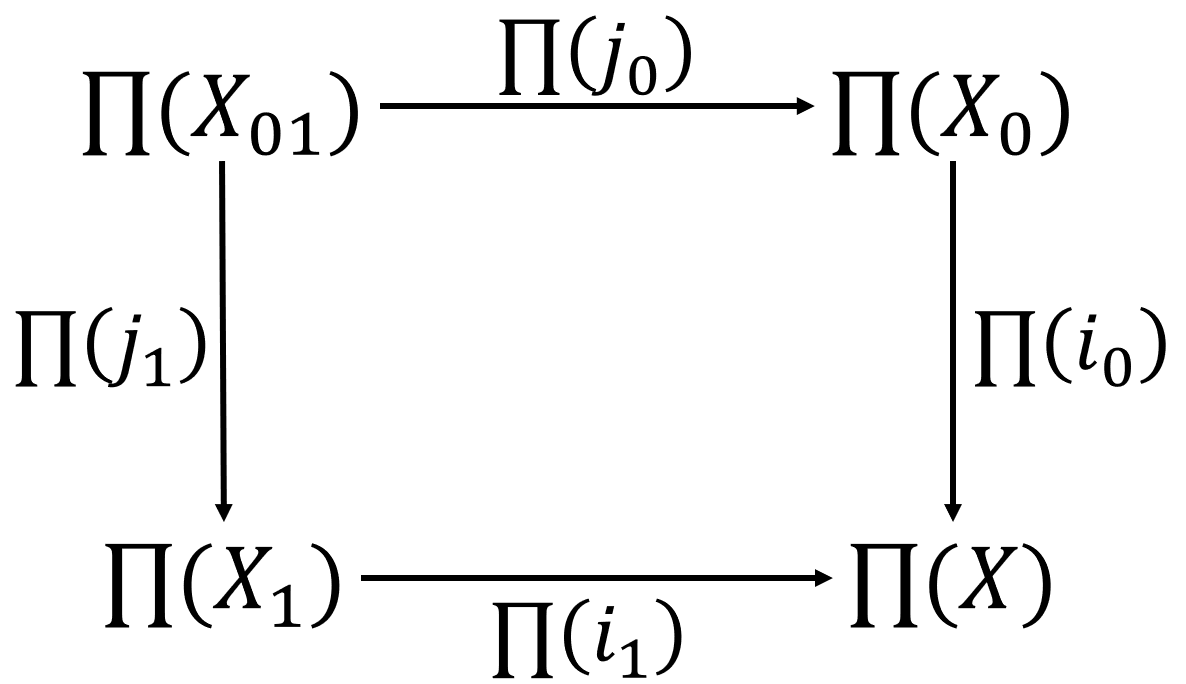
由于定理的证明过程较长, 限于篇幅, 此处也就不附证明. 详细的证明过程可参考庄晓波老师的视频:
1. (36)Seifert&van Kampen定理groupoid版本
2. (37)Seifert&van Kampen定理