最近学习庄晓波老师的代数拓扑课程时时常会出现书上未介绍过的术语, 故以此文作为记录.
参考材料
1. Universal property
2. exact_sequence.pdf
1. 典则嵌入
即单射.
2. Universal Mapping Property
设$F: \mathcal{C} \to \mathcal{D}$为范畴$\mathcal{C}, \mathcal{D}$之间的函子, $X$为$\mathcal{D}$中的一个对象, $A, A’$均为$\mathcal{C}$中的对象, 则函子$F$分别将$A, A’$与$h \in \mathcal{C}$映射到$\mathcal{D}$中的$F(A)$, $F(A’)$与$F(h)$.
$\\$ 一个从$X$映射到$F$的Universal Morphism是$\mathcal{D}$中唯一的对$(A, u:
$$ X \to F( $$ A))$, 该对具有如下性质, 通常称之为Universal Mapping Property: 对于$\mathcal{D}$中任意形式为$f: X \to F(A’)$的态射, 存在$\mathcal{C}$中唯一的态射$h: A \to A’$, 使得如下交换图表成立.
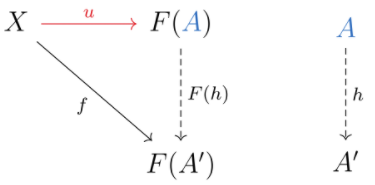
我们可以将上述概念对偶化. 一个从$F$映射到$X$的Universal Morphism是$\mathcal{D}$中唯一的对$(A, u: F(A) \to X)$, 该对具有如下性质, 通常称之为Universal Mapping Property: 对于$\mathcal{D}$中任意形式为$f: F(A’) \to X$的态射, 存在$\mathcal{C}$中唯一的态射$h: A’ \to A$, 使得如下交换图表成立.

3. Fibered Coproduct与Cocartesian图表
设$\mathcal{C}$为一个范畴, 设$f: Z \to X$, $g: Z \to Y$, $f$与$g$的Fibered Coproduct是指数据$(W, p_1, p_2)$, 其中$W \in \mathcal{O}b(\mathcal{C})$, $p_1: X \to $$ W$, $p_2: Y \to W$, 且$(W, p_1, $$ p_2)$满足如下约束: 对于任意使得下面图表可交换的两个映射$u: X \to U$, $v: Y $$ \to U$,
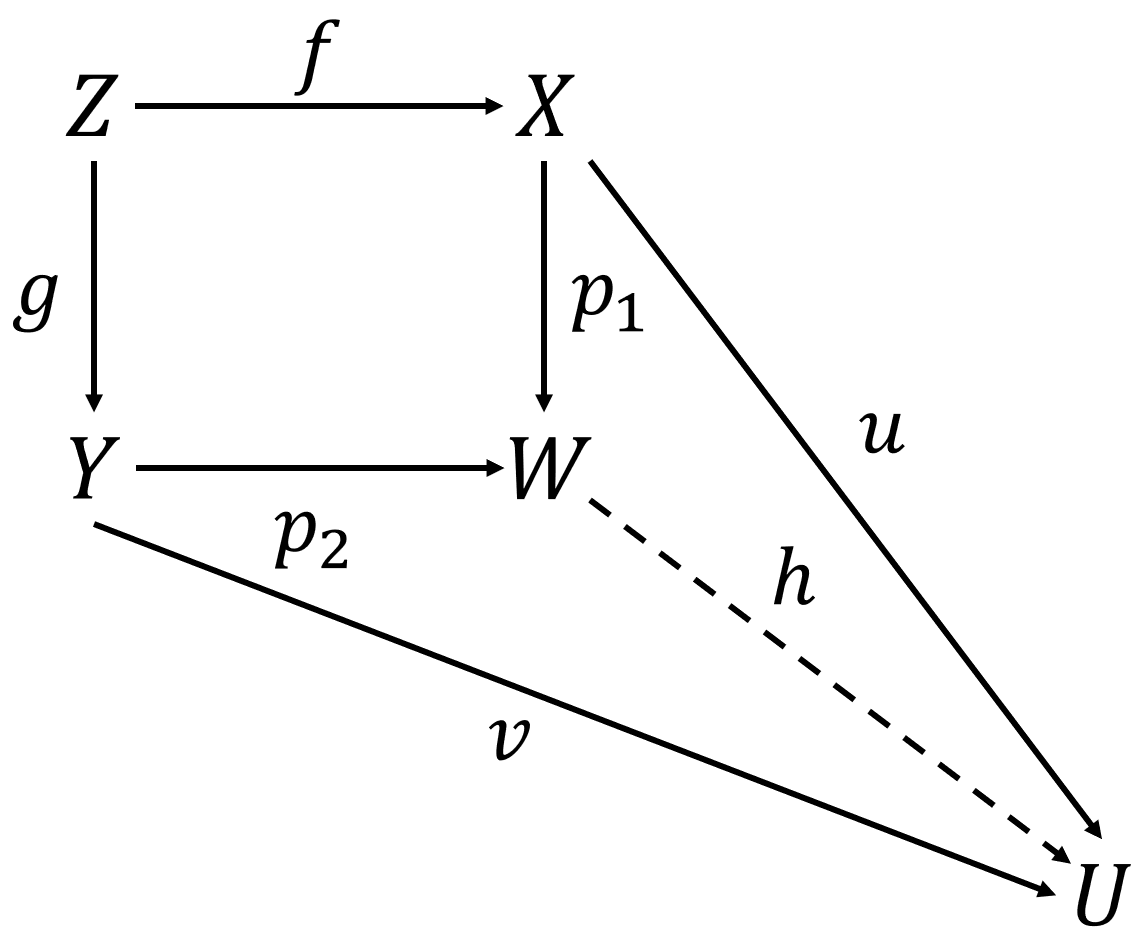
存在一个唯一的态射$h: W \to U$, s.t. $h \circ p_1 = u$, $h \circ p_2 = v$. 此时, 称如下图表为一个Cocartesian图表.
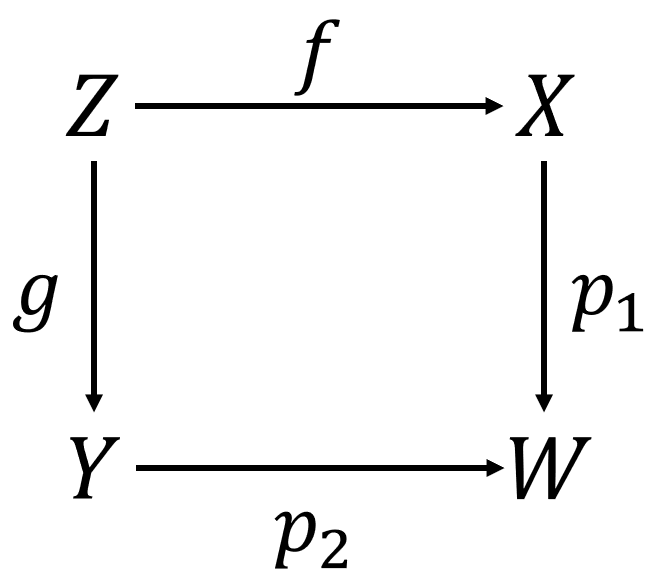
Rmk1. 将以上论述中的箭头全部反向后, 即可得Fibered Product的定义.
$\\$ Rmk2. 在范畴$\mathcal{C}$中$f$与$g$的Fibered Coproduct在差一个同构的意义下是唯一的.
4. 自由群
在之前的文章中其实已经介绍过自由群的定义了, 此处再介绍一下在庄晓波老师的代数拓扑课程中提及的自由群的定义, 这里是利用自由积来定义自由群的.
$\\$ 设$S$为一个集合, $S$上的自由群$F(S)$定义为:$$F(S) := *_{\alpha \in S} \left \langle \alpha \right \rangle,$$其中$\left \langle \alpha \right \rangle = \{ \alpha^n \ | \ n \in Z \}$是一个无限循环群.
5. 短正合序列
5.1 正规子群与商群
首先我们回顾正规子群的定义. 设$H$是$G$的子群, 则若对于$\forall g \in G$都有$gHg^{-1} $$ = H$, 则$H$称为$G$的正规子群. 正规子群的定义立刻导致两个推论, 即
$\\$ a) 左右陪集相同, $gH = Hg$, 因此左右陪集空间是一样的, 并定义为商空间$G / $$ H$.
$\\$ b) 相应的商空间$G / H$可以从$G$继承群乘法结构, 并构成商群.
$\\$ 其中, 我们注意到两个近乎平凡的论断, 第一是”$H$是$G$的子集”, 第二是”$G / H$的元素$[gH]$都对应一个$G$中$H$的陪集$gH$”. 我们可以把这两个论断表达为, 存在一个单射(Injection), 称为”映入映射”(Inclusion Map) $\imath : H \to G$, 以及满射(Surjection), 称为”投影映射”(Projection) $\pi : G \to G / H$, 使得$\pi(gH) = $$ [gH]$(其中$\imath$和$\pi$分别是”Inclusion” 和”Projection” 的希腊首字母). 那么根据同态核与$G / H$的定义, 我们有$$Im \imath = ker \pi,$$因为$Im \imath = H \subset G$正是被视为$G / H$中的单位元, 或者等价地说, 整个$Im \imath$被$\pi$映射为单位元.
5.2 短正合序列
上面这些论断与关系式可以被重新组合为”短正合序列”(Short Exact Sequence, 有时”正合” 也翻译为”恰当”) 的概念.
$\\$ 考虑四个首尾相接的同态映射,$$\{ e \} \overset{\varphi_0}{\longrightarrow} G_1 \overset{\varphi_1}{\longrightarrow} G_2 \overset{\varphi_2}{\longrightarrow} G_3 \overset{\varphi_3}{\longrightarrow} \{ e \},$$该序列是”正合的” 说的是该序列每两个相邻映射都满足$$Im \varphi_i = ker \varphi_{i + 1}.$$