最近工作上还是发生了蛮多事的, 最主要的变动就是自己在的项目组被”砍”了…… 凡事都具备两面性, 这件事也不例外. 尽管十分不舍得目前的项目组, 但自己也借这个机会成功转为引擎研发, 算是较彻底地告别了GamePlay. 希望这是一个好的契机与开始叭~ 下周一还有天美面试, 尽管现在已经对跳槽去天美这件事不是很上心了, 因为更倾向于在网易继续学习与提升自己. 好了, 话不多说, 进入正题, 本文主要是Seifert & Van Kampen定理的相关习题解答.
参考材料
1. Understanding how to compute $\pi_1(S^1 \vee S^2)$
2. Fundamental group of a torus with points removed
3. 专题讨论: 三维球面
4. The Fundamental Group of the Real Projective Plane
1. 在拓扑空间$X$和球面$S^2$上各取一点, 然后把这两点拓扑地粘合, 得到一点并$X $$ \vee S^2$, 证明其基本群同构于$\pi_1(X)$(注意, $S^2$不一定是它在$X \vee S^2$中的邻域的形变收缩核, 因此不能直接应用Van Kampen定理).
$\\$ 证: 尝试证明一个更具一般性的命题: 若拓扑空间$A$为可缩空间, 与拓扑空间$B$相交于点$p$, 则$\pi_1(A \cup B) \cong \pi_1(B)$.
$\\$ 设$\gamma$为$A \cup B$中的一条闭道路(非点道路), $e_p^A$为拓扑空间$A$中以$p$为基点的点道路, $e_p^B$为拓扑空间$B$中以$p$为基点的点道路, 对其进行分类讨论.
$\\$ $\cdot$ 闭道路$\gamma$的基点$b$($\ne p$) 位于拓扑空间$A$内, 且$\gamma \cap B = \emptyset$或$\gamma \cap B $$ = \{ p \}$, 则闭道路$\gamma$所在的闭道路类$\left \langle \gamma \right \rangle = \left \langle e_p^A \right \rangle$, 它与$\pi_1(B)$中的闭道路类$\left \langle e_p^B \right \rangle$一一对应.
$\\$ $\cdot$ 闭道路$\gamma$的基点$b$($\ne p$) 位于拓扑空间$A$内, 且$\gamma \cap B \ne \emptyset$, 则可将闭道路$\gamma$分解得$\gamma = \gamma_1 \cup \eta_1 \cup \cdots \cup \eta_n \cup \gamma_n$, 其中$\gamma_i \cap A = \{ p \}$, $\eta_i \cap B = $$ \{ p \}$. 由于拓扑空间$A$为一个可缩空间, 故闭道路$\gamma$同伦于以$p$为基点的闭道路$\eta_1 \cup \cdots \cup \eta_n$, 从而$\left \langle \gamma \right \rangle $$ = \left \langle \eta_1 \cup \cdots \cup \eta_n \right \rangle$, 与$\pi_1(B)$中的一个闭道路类形成一一对应.
$\\$ $\cdot$ 闭道路$\gamma$的基点$b = p$, 则$\gamma \cap A \ne \emptyset$, $\gamma \cap B \ne \emptyset$. 我们将闭道路$\gamma$分解得$\gamma =
$$ \gamma_1 \cup \eta_1 \cup \cdots \cup \eta_n \cup \gamma_n$, 其中$\gamma_i \cap A = \{ p \}$, $\eta_i \cap B $$ = \{ p \}$. 由于拓扑空间$A$为一个可缩空间, 故闭道路$\gamma$同伦于以$p$为基点的闭道路$\eta_1 \cup \cdots \cup \eta_n$, 从而$\left \langle \gamma \right \rangle = \left \langle \eta_1 \cup \cdots \cup \eta_n \right \rangle$, 与$\pi_1(B)$中的一个闭道路类形成一一对应.
$\\$ $\cdot$ 闭道路$\gamma$的基点$b$($\ne p$) 位于拓扑空间$B$内, 且$\gamma \cap A = \emptyset$或$\gamma \cap A $$ = \{ p \}$, 则闭道路$\gamma$所在的闭道路类$\left \langle \gamma \right \rangle$通过一个投影映射与$\pi_1(B)$中的一个闭道路类形成一一对应.
$\\$ $\cdot$ 闭道路$\gamma$的基点$b$($\ne p$) 位于拓扑空间$B$内, 且$\gamma \cap A \ne \emptyset$, 则可将闭道路$\gamma$分解得$\gamma = \gamma_1 \cup \eta_1 \cup \cdots \cup \eta_n \cup \gamma_n$, 其中, $\gamma_i \cap A = \{ $$ p \}$, $\eta_i \cap B $$ = \{ p \}$. 由于拓扑空间$A$为一个可缩空间, 故闭道路$\gamma$同伦于以$p$为基点的闭道路$\eta_1 \cup \cdots \cup \eta_n$, 从而$$\left \langle \gamma \right \rangle = \left \langle \eta_1 \cup \cdots \cup \eta_n \right \rangle,$$与$\pi_1(B)$中的一个闭道路类形成一一对应.
2. 写出挖去两个点的环面的基本群的一个表出.
$\\$ 解: 我们先考虑挖去一个点$p$的环面的基本群的一个表出. 从环面多边形表示的角度出发, 环面$T^2 = Q / \sim$, 其中, $Q := [-1, 1] \times [-1, 1]$, 对于$x \in [-1, 1]$有$(x, -1) \sim (x, 1)$, 对于$y \in [-1, 1]$, 如下图所示.
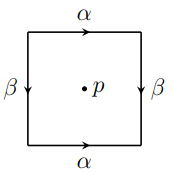
此外, 假设$p = (0, 0)$位于四边形中心. 易知$Q \backslash \{ p \}$可通过如下同伦形变收缩至四边形的边界$\partial Q$,$$H((x, y), t) = (1 – t)(x, y) + tb(x, y),$$其中, $b(x, y) \in \partial Q$是$\partial Q$与从$p$出发经过$(x, y)$的射线的唯一的交点. 故$(Q / $$ \sim) \backslash \{ p \}$的基本群与$\partial Q / \sim$的基本群是同构的. 又$\partial Q / $$ \sim$同胚于两个圆周的一点并(又称2圆束), 故我们可通过Van Kampen定理得到$$\pi_1(T^2 \backslash \{ p \}) = \pi_1(\partial Q / \sim) = \pi_1(S^1 \vee S^1) \\ = \pi_1(S^1) * \pi_1(S^1) = Z * Z.$$同理可得, 当从环面挖去$n$个点后, 易知$\partial Q / \sim$同胚于$n + 1$个圆周的一点并(又称$n + 1$圆束), 从而挖去$n$个点的环面的基本群的一个表出为$\left \langle \gamma_1, \cdots, \gamma_{n + 1} \ | \ \right \rangle$, 其中每个$\gamma_i$是绕第$i$个圆周一圈的闭道路类, 如下图所示.
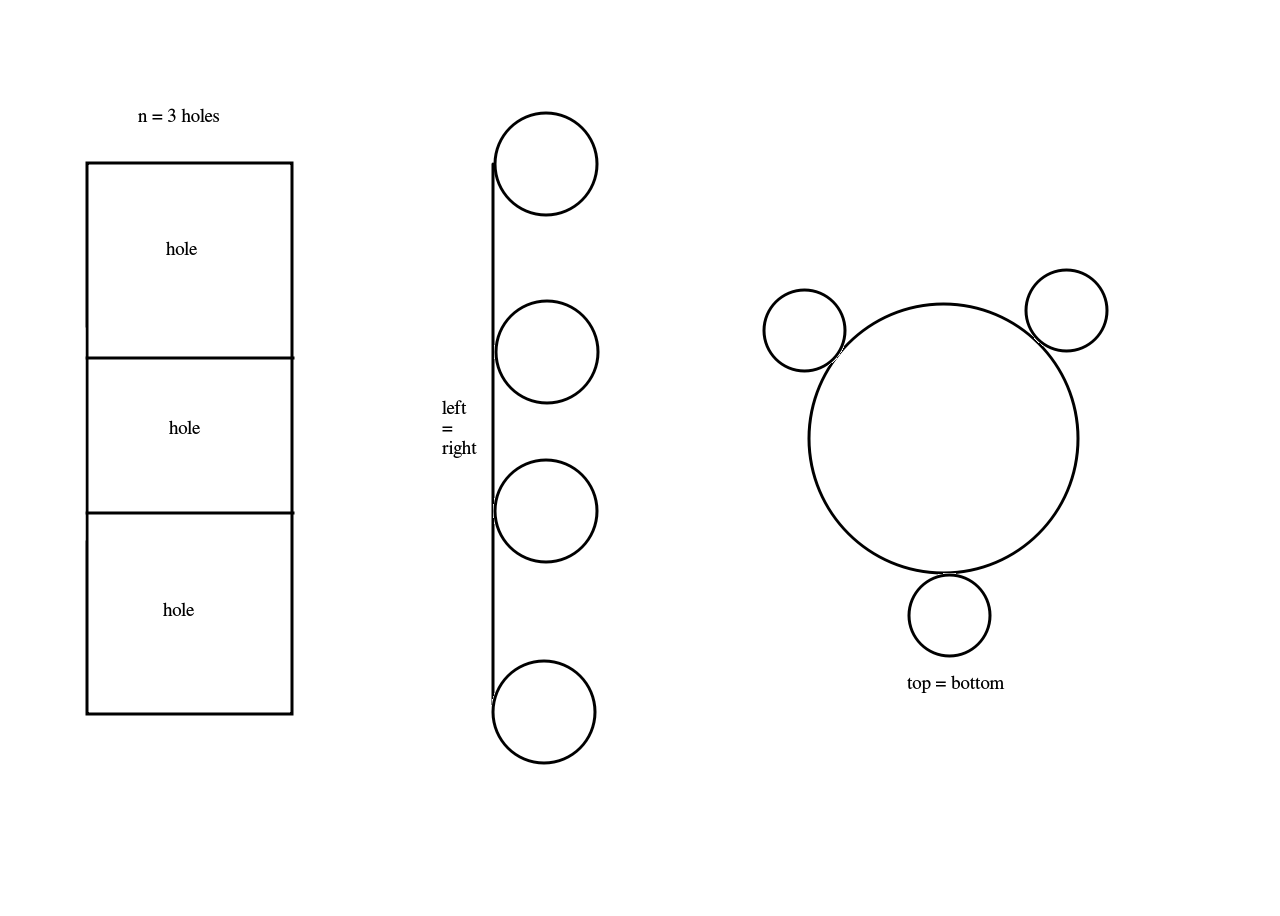
3. 设$M$为三维流形, $p \in M$, 证明在$M$中任取基点$x_0 \ne p$, $$\pi_1(M, x_0) \cong \pi_1(M \backslash \{ p \}, x_0).$$证: 取$U$为$p$的同胚于开实心球的邻域, 记$V = M \backslash \{ p \}$, 由于开实心球为$E^3$中的凸子集, 故其基本群为平凡群(相关证明可参考基本群相关习题), 从而$U$的基本群亦为平凡群. 又$U \cap V$同胚于一个去心的开实心球, 它可通过映射$F: $$ [0, 1] \times $$ (U \cap V) \to S^3$形变收缩至$S^3$, 映射$F$定义如下所示,$$F(\lambda, x) = (1 – \lambda)x + \lambda \frac{x}{\left \| x \right \|}.$$$\therefore \pi_1(U \cap V) \cong \pi_1(S^3) = \{ \left \langle e_{S^3} \right \rangle \}$, 其中, $e_{S^3}$为$S^3$中的点道路. 最后应用Seifert & Van Kampen定理, 命题即可得证.
4. 仿照环面基本群的计算过程, 写出射影平面的基本群的一个计算过程以及结果.
解: 令$RP^2 = A \cup B$, 其中$A$为红色圆盘, $B$为蓝色环, $A$与$B$的交集为紫色的小环, 如下图所示.
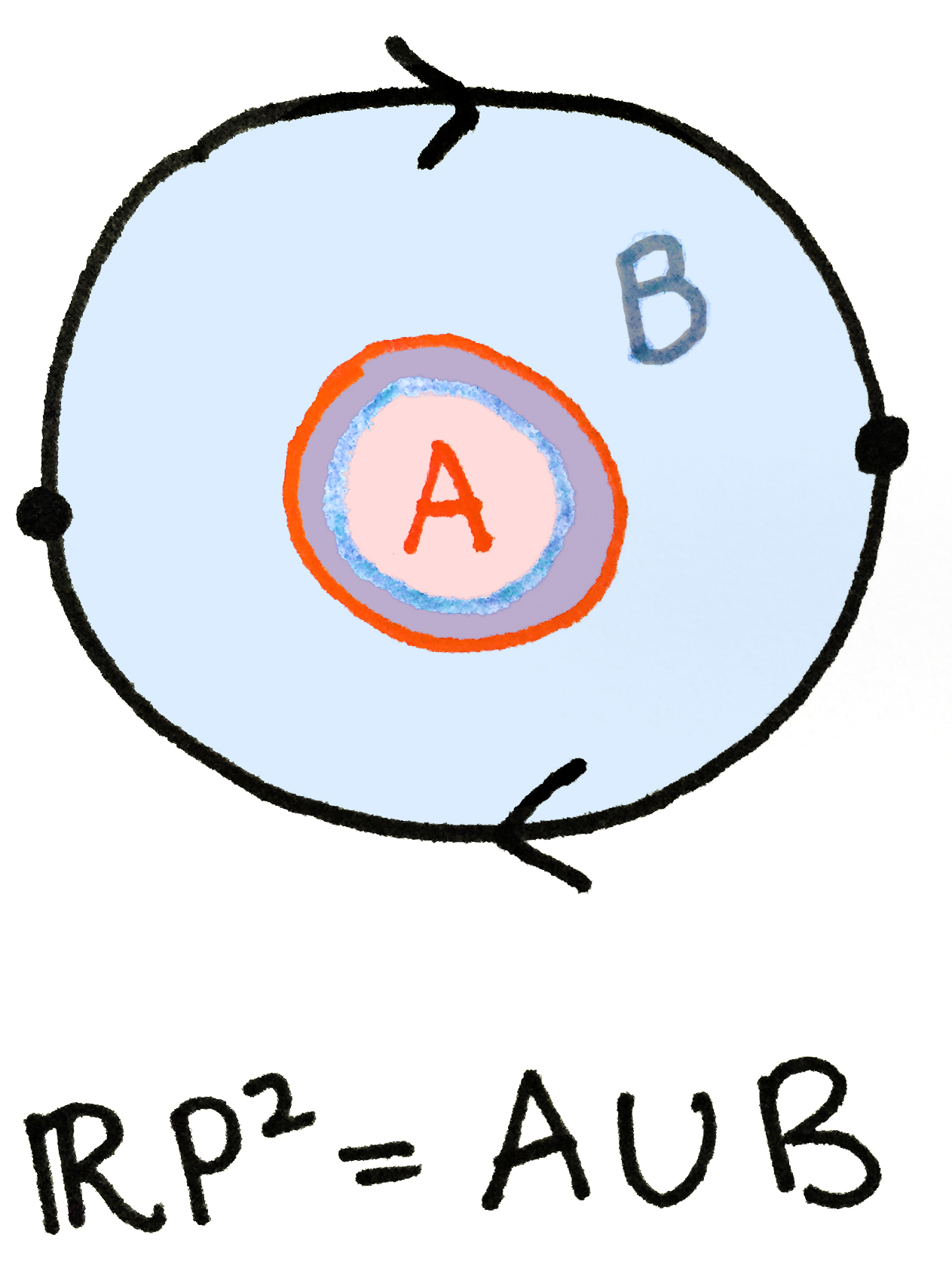
由Seifert & Van Kampen定理可得$$\pi_1(RP^2) = \pi_1(A) *_{\pi_1(A \cap B)} \pi_1(B).$$接下来分别计算$\pi_1(A), \pi_1(B)$与$\pi_1(A \cap B)$. 由于$A$是可缩的, 故$$\pi_1(A) \cong \{ \left \langle e_A \right \rangle \} = \left \langle \ \emptyset \ | \ \emptyset \ \right \rangle,$$其中, $e_A$为$A$中的点道路. 同理, 由于$A \cap B$为一个环, 其可形变收缩至一个圆圈, 不妨设其生成元为$\gamma$, 则$$\pi_1(A \cap B) \cong Z = \left \langle \gamma \ | \ \emptyset \ \right \rangle.$$而对于$\pi_1(B)$, 注意到$B$是由$RP^2$减去一个圆盘得到的, 故$B$同胚于一个莫比乌斯带. 而莫比乌斯带可形变收缩至一个圆圈(通过一个简单的投影), 不妨设其生成元为$b$, 则$$\pi_1(B) \cong Z = \left \langle b \ | \ \emptyset \ \right \rangle.$$从而我们有$$\pi_1(RP^2) = \{ \left \langle e_A \right \rangle \} *_Z Z.$$由自由积的定义, 我们列出所有相关的生成元与生成关系, 并将上式改写为如下形式:

其中, $i_{A_*} : \pi_(A \cap B) \to \pi_1(A)$是由含入映射$i_A : A \cap B \mapsto A$诱导的同态映射, $i_{B_*} : \pi_(A \cap B) \to \pi_1(B)$是由含入映射$i_B : A $$ \cap B \mapsto B$诱导的同态映射.接下来我们仅需计算映射$i_{A_*}, i_{B_*}$即可. 而映射$i_{A_*}$是容易计算的, 因为$\pi_1(A) $$ = \{ \left \langle e \right \rangle \}$, 故$i_{A_*}$是一个平凡映射, 即$i_{A_*}(\left \langle \gamma \right \rangle) = \left \langle e_A \right \rangle$.
$\\$ 但对于生成元$\gamma$在映射$i_{B_*}$下的像, 我们需要考虑生成元$b$与生成元$\gamma$之间的关系(一个同态映射可由定义域与值域的生成元决定), 示意图如下所示.

其中, 生成元$b$为莫比乌斯带中位于中心处的圆圈, 生成元$\gamma$为其边界圆. 由上图可知, $i_{B_*}(\left \langle \gamma \right \rangle) = b^2$.
$\\$ 综上所述, 我们可以得到$\pi_1(RP^2)$的表出, 即$$\pi_1(RP^2) = \left \langle b \ | \ b^2 \right \rangle = Z / 2Z.$$Q.E.D.