今天总算把新的房间基本打扫完毕了, 心情十分愉快~ 下周就是五一假期了, 现在杭州的疫情形势感觉是暗流涌动, 但愿能够顺利回家叭=.= 最近在学习Jordan曲线定理, 虽然其证明还没看完, 但发现了一个很有趣的算法应用——判断点是否在多边形内部的算法, 同时这也是最近工作内容中用到的一个算法, 因此想要记录一下相关算法要点.
参考材料
1. 改进的point in polygon problem算法介绍
Contents
背景知识
点和多边形的位置问题(Point-In-Polygon(PIP) Problem), 一般指的是给定二维平面上的一个点$Q$以及一个多边形$P$,怎样判断点$Q$是位于多边形$P$内部还是外部. 该算法在计算机图形学, 地理空间信息学等领域有广泛的应用. 目前有两种通用的算法实现: Ray Casting Algorithm(又称Even-Odd算法) 和Winding Number Algorithm.
$\cdot$ Ray Casting Algorithm
从$Q$向无穷远点发射一条射线, 计算该射线和多边形的边相交的次数, 如果是奇数次, 则点在多边形内部; 如果是偶数次, 则点在多边形外部. 该算法的理论依据是Jordan曲线定理: 设$\gamma: S^1 \to E^2$是一个嵌入, 则$E^2 \backslash \gamma(S^1)$存在唯一一个有界道路分支$U$, 并且$U$以$\gamma(S^1)$为边界, 即$\overline{U} \backslash U^{\circ} = \gamma(S^1)$.
根据Jordan曲线定理, 可以对算法有直观的解释: 对于给定点$Q$和无穷远点间$S$的连线$QS$,由于$S$必然位于多边形$P$外部, 而$QS$和多边形的每个交点$K$都是一个外部和内部切换的临界点:
1. 如果是奇数个交点, 从$S$出发, 切换过程必然是: $S$(外部) –>(内部) –>(外部) $\cdots$–>(内部)–>$Q$, 这样$Q$必然位于$P$内部.
2. 如果是偶数个交点, 从$S$出发, 切换过程必然是: $S$(外部) –>(内部) –>(外部) $\cdots$–>(外部) –>$Q$, 这样$Q$必然位于$P$外部.
$\cdot$ Winding Number Algorithm
Winding Number Algorithm又称为转角累加法, 知乎上有一个比较直观的解释如下:
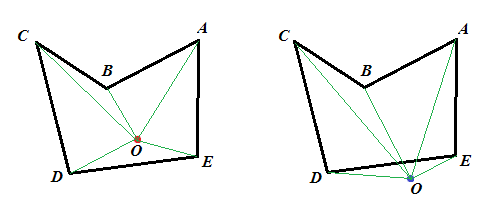
给多边形的顶点依次编号(如上图中为$A, B, C, D, E$), 称待判断的点为$O$. 依次考察角$AOB, BOC, COD, DOE, EOA$. 这里的角均取小于180度的那一侧, 并均为有向角, 我们规定逆时针为正, 顺时针为负. 上面左图中, 五个角都是正的; 右图中, 角DOE是负的. 把所有的角累加起来, 我们发现左图中角度之和为360度, 右图为零.
形象一点儿理解, 就是你站在$O$处, 转身用目光把整个多边形扫描一遍. 若你转了奇数圈, 则你在多边形内; 若你转了偶数圈, 则你在多边形外.
对于简单多边形(边不自交的多边形), 拓扑上即为与$S^1$同胚的图形, 上面的两种算法通常能得到相同的结果. 对于边相交的非简单多边形(此时也无法直接使用Jordan曲线定理), 内部与外部通常有不同的定义: 有的把重叠部分根据异或(XOR) 原则定义为外部, 有的则把重叠部分根据或(OR) 原则定义为内部. 由于一般的Ray Casting算法不能够处理射线和顶点相交的情形以及射线和多变形边重合等特殊情形, 因此接下来简要介绍一种简单有效的改进了的Ray Casting算法.
算法介绍
该算法由Michael Galetzka和Patrick Glauner于2012年提出, 2017年发表于Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications(VISIGRAPP 2017). 值得一提的是, Michael Galetzka还就职于Epic Games, 保不准他提出的这个算法已经应用在UE上了~
由于点$Q$与多边形$P$(顶点为$p_1, p_2, \cdots, p_n$) 位于二维平面上, 可以考虑将$Q$和$P$通过坐标平移, 使$Q$平移到坐标原点而其和$P$的相对位置不变, 显然平移不会改变点$Q$与多边形$P$的位置关系(在多边形内或外), 下面算法主要是针对平移后的情形进行说明, 算法步骤如下:
1. 判断$Q$是否位于是$P$的顶点或者位于$P$的边上, 如果是, 点$Q$在多边形内部.
2. 在顶点集合$P$中寻找不在$x$轴上的顶点, 如果找不到, 点$Q$在多边形外部. (注: 根据步骤1, $Q$不在$P$的顶点或者边上, 而找不到不在$x$轴上的点说明多边形$P$的点都在$x$轴上, 而$Q$位于原点, 说明$Q$在$P$的外部.)
3. 设$i = 1$, 从点$p_s$开始通过重复下面步骤直到所有的顶点都被访问到:
$\quad$a) 判断点$p_{s + i}$是否位于$x$轴上, 如果在, 递增$i$, 如果$s + i > n$, 那么将$i$设置为$-s$, 从$p_0$开始继续寻找, 直到找到一个不位于$x$轴上的点$p_{s + i}$为止.
$\quad$b) 根据步骤a中的查找过程, 采取下面的操作:
$\quad \quad$i) 如果步骤a中找时没有Skip掉任何顶点, 那么判断从$p_s$到$p_{s + i}$的线段是否和$x$轴的正半轴相交, 如相交, 交点个数加1;
$\quad \quad$ii) 如果步骤a中找时Skip掉至少一个$x$轴坐标为正的顶点, 那么判断从$p_s$到$p_{s + i}$的线段是否和整个$x$轴相交, 如相交, 交点个数加1;
$\quad \quad$iii) 如果步骤a中找时Skip掉至少一个$x$轴坐标为负的顶点, 不做任何操作; (注: 不可能同时Skip掉位于$x$轴正半轴和$x$轴负半轴的点, 如果有, 说明$Q$位于多边形的边上, 步骤1就返回了)
$\quad$c) $p_{s + i}$为下一轮迭代的起点.
4. 判断交点个数是奇数还是偶数, 如果是奇数, 说明点$Q$位于多边形$P$内部; 如果是偶数, 说明点$Q$位于多边形$P$外部.
至于算法的正确性证明, 可参考论文A Simple and Correct Even-Odd Algorithm for the Point-in-Polygon Problem for Complex Polygons
不难发现, 所有点均只访问一遍, 时间复杂度为$O(n)$, 作者也在这里给出了在点的数值类型为整型情形下的一个实现, 若后面有空, 自己可以尝试将其扩展到浮点数下的情形.