周五去医院做了一次体检复查, 接下来就要开启一个月的嗑药历程了. 哎, 希望真的只嗑一个月叭, 身体是革命的本钱, 对自己好点~ 本文算是群作用一节的番外篇, 介绍一下双曲几何在计算机可视化领域的一个应用——双曲树, 或许也能从中得到灵感.
参考材料
1. A Focus Context Technique Based on Hyperbolic Geometry for Visualizing Large Hierarchies
2. 凯莱-克莱因模型
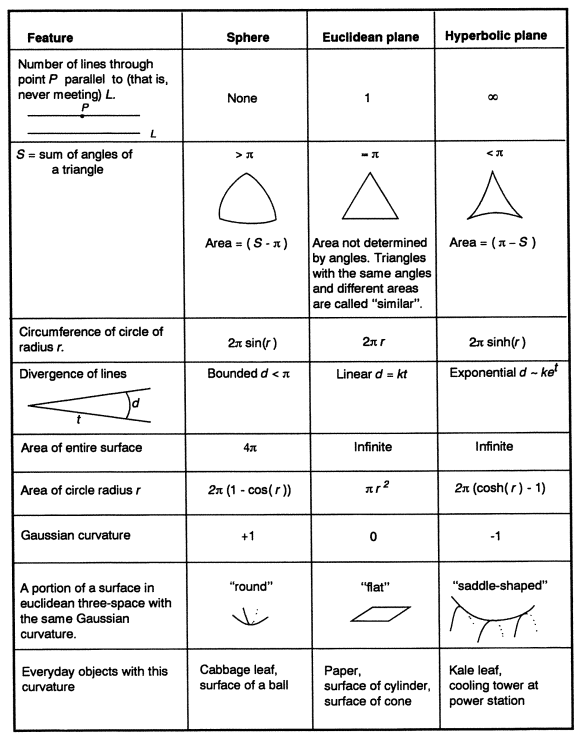
球面, 欧几里得平面与双曲平面是三种常见的几何模型, 下图总结了这三种几何模型的特点.
1. 双曲平面
通常我们把双曲平面理解成不含边界的单位圆盘$$H^2 = \{ z \in C \ | \ |z| < 1 \}$$带上双曲度量$$d(z_1, z_2) = cosh^{-1}(1 + \frac{2|z_1 - z_2|^2}{(1 - |z_1|^2)(1 - |z_2|^2))},$$其中$cosh^{-1}$表示反双曲余弦, 即任取实数$t > 1$,$$cosh^{-1}(t) = ln(t + \sqrt{t^2 – 1}).$$这个空间称为双曲平面的Poincare圆盘模型, 不过提出这个模型的却不是Poincare而是Beltrami. 双曲度量的公式看上去很复杂, 对我们建立几何直观好像不是什么好事情, 但是双曲等距变换却非常容易刻画. 一个自同胚$f: H^2 \to $$ H^2$如果满足$d(p, q) = d(f(p), f(q))$, 则称之为双曲等距变换. 可以证明, 任何一个双曲等距变换都具有$z \mapsto $$ \frac{az + \bar{b}}{bz + \bar{a}}$或者$z \mapsto \frac{a\bar{z} + \bar{b}}{b\bar{z} + \bar{a}}$的形式. 单位圆盘$H^2$的直径以及与边界圆周垂直的圆弧统称为双曲直线, 双曲等距变换一定会把双曲直线变成双曲直线, 并且保持两条相交双曲直线的夹角不变.
2. 双曲树的实现
双曲树的使用可参考视频 2:08 2:09 / 3:14 Visualizing Large Trees Using the Hyperbolic Browser, 其底层实现是以Poincare圆盘模型为理论基础的. 我们用圆心位于原点的单位圆盘上的点来表示双曲空间中的一个点, 此时双曲平面上的的刚性变换被转换为单位圆盘上的保圆变换.
$\\$双曲树使用的双曲变换为关于复数$z$的复变函数, 它具有如下形式:$$z_{(P, \theta)} = \frac{\theta z + P}{1 + \overline{P}z},$$其中, $P$与$\theta$均为复数, $|P| < 1$且$|\theta| < 1$, $\overline{P}$表示$P$的共轭复数. 个人认为此处分母处的1应为1个复数, 因为$\overline{P}z$并不一定是一个实数. 该变换的几何意义是将复数$z$绕原点旋转复数$\theta$对应的旋转角度, 然后将原点移至$P$点. 但存在疑问的一点是, 该变换并不满足上面提到的双曲等距变换形式.
$\\$两次双曲变换$z_{(P_1, \theta_1)}, z_{(P_2, \theta_2)}$的复合双曲变换$z_{(P, \theta)}$中的$P, \theta$计算如下:$$P = \frac{\theta_2 P_1 + P_2}{\theta_2 P_1 \overline{P_2} + 1}, \\ \theta = \frac{\theta_1 \theta_2 + \theta_1 \overline{P_1} P_2}{\theta_2 P_1 \overline{P_2} + 1}.$$由于舍入误差, 新得到的$\theta$的模不会严格等于1, 特别是在对边界附近的点进行变换时这个问题会被放大, 因此总是需要对新得到的$\theta$进行重新归一化.
$\\$此外, 由于图形硬件支持$3 \times 3$的矩阵乘法, 使用Klein模型(亦称射影模型) 能够获得更高的计算性能, 因为刚性变换可以利用齐次坐标上的线性运算进行表示. 接下来可通过两种方式将Klein模型上的点重新映射回Poincare圆盘模型上.
$\\$a) 通过$r_p = r_k / (1 + \sqrt{1 - r_k^2})$重新计算距离原点的距离.
$\\$b) 设$s$为Kelin模型上模小于1的一点, 则Poincare圆盘模型上的对应点为$$u = \frac{s}{1 + \sqrt{1 - s \cdot s}} = \frac{(1 - \sqrt{1 - s \cdot s})s}{s \cdot s}.$$