这周在工作上被一个模型匹配的问题卡了两三天, 有点难受, 虽然后面发现更多的是来自于Houdini Api的问题, 希望下周能够尽快解决叭~ 本文主要研究上篇文章中提到的使用Klein模型(亦称射影模型) 能够获得更高的计算性能的技巧.
参考材料
1. Cayley–Klein metric
2. Bi Y, Fan B, Wu F. Beyond mahalanobis metric: cayley-klein metric learning[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 2339-2347.
3. 多视图几何总结——等距变换、相似变换、仿射变换和射影变换
其中, 参考材料1是一篇关于Cayley-Klein度量的Wiki, 这篇Wiki是从绝对几何的角度出发的, 由于自己没学过绝对几何, 因此这篇Wiki看得一脸懵逼; 而参考材料2是一篇关于Cayley-Klein度量的应用的论文, 无论是专业性还是易读性都是高于前者的, 对于应用专业出身的自己也比较友好, 因此本文内容也主要参考自参考材料2.
1. 定义
给定一个可逆的对称矩阵$\Psi \in R^{(n + 1) \times (n + 1)}$, $x, y \in R^n$的双线性表示$\psi(x, y)$为:$$\psi(x, y) = (x^T, 1) \Psi \binom{y}{1}, \forall x, y \in R^n.$$为了方便书写, 我们接下来将$\psi(x, y)$记为$\psi_{xy}$.
$\\$ 若矩阵$\Psi$是正定矩阵, 则$\psi_{xy} > 0$, 我们可以定义$\rho_E(x, y): R^n \times $$ R^n \to R^+$为:$$\rho_E(x, y) = \frac{k}{2i} log(\frac{\psi_{xy} + \sqrt{\psi_{xy}^2 – \psi_{xx}\psi_{yy}}}{\psi_{xy} – \sqrt{\psi_{xy}^2 – \psi_{xx}\psi_{yy}}}), k > 0.$$若矩阵$\Psi$是不定矩阵, 令$B^n = \{ x \in R^n | \psi_{xx} < 0 \}$, 我们可以定义$\rho_H(x, y): $$ B^n \times B^n \to R^+$为:$$\rho_H(x, y) = \frac{k}{2} log(\frac{\psi_{xy} + \sqrt{\psi_{xy}^2 - \psi_{xx}\psi_{yy}}}{\psi_{xy} - \sqrt{\psi_{xy}^2 - \psi_{xx}\psi_{yy}}}), k > 0.$$可以证明, $\rho_E(x, y)$与$\rho_H(x, y)$分别为$R^n$与$B^n$的度量, 因为它们均满足如下三条度量公理:
$\cdot$ $\rho(x, y) \ge 0$(非负性).
$\cdot$ $\rho(x, y) = 0 \Leftrightarrow x = y$(非退化性).
$\cdot$ $\rho(x, y) = \rho(y, x)$(对称性).
$\cdot$ $\rho(x, z) \le \rho(x, y) + \rho(y, z)$(三角不等式性).
$\\$ $(R^n, \rho_E)$被称为椭圆几何空间, $(R^n, \rho_H)$被称为双曲几何空间. $\rho_E$与$\rho_H$一起被称为Caley-Klein度量. 为方便起见, 可统一写为如下形式:$$\rho(x, y) = \frac{k}{2} \left | log(\frac{\psi_{xy} + \sqrt{\psi_{xy}^2 – \psi_{xx}\psi_{yy}}}{\psi_{xy} – \sqrt{\psi_{xy}^2 – \psi_{xx}\psi_{yy}}}) \right | , k > 0,$$其中$1 / k$($-1 / k$) 与椭圆(双曲) 空间的曲率有关.
$\\$ 根据上述定义, Caley-Klein度量只依赖于对称矩阵$\Psi$. 换句话说, 给定一个对称矩阵, 便可以诱导出一个特定的Caley-Klein度量. 因此, 对称矩阵$\Psi$被称为Caley-Klein度量矩阵.
2. 不变性
几何学的主要内容是研究在各种变换群作用下的几何不变量. 其中, 等距变换的不变量为长度, 角度与面积; 相似变换的不变量为长度的比率, 角度的比率与面积的比率; 仿射变换的不变量为平行线段的长度比, 平行线与面积比, 仿射变换是保持无穷远点线不变形的最一般的线性变换, 这句话的意思就是说, 例如射影变换是会将无穷远点变成有限点, 正因为如此, 射影变换可以完成消除透视失真的操作, 使得原本平行的直线不再平行, 而仿射变换之后平行直线仍然平行, 因为其不改变无穷远点的性质; 射影变换是非齐次坐标的一般的非奇异线性变换与平移的复合, 其不变量为共点, 共线, 接触的阶还有长度的比率的比率. 此处附上一张多视图几何中关于几种变换的总结表.

接下来介绍几个关于Caley-Klein度量的不变量的命题.
命题1 给定两点$x, y \in R^n(B^n)$, 令$z_+$与$z_-$为$x, y$所在的直线与二次曲面$\Omega = \{ z | \psi(z, z) = 0 \}$的两个交点, 则$$\rho(x, y) = \frac{k}{2} \left | log \ r(xy, z_+ z_-) \right |,$$其中$r(xy, z_+ z_-)$为四点$\{ x, y, z_+, z_- \}$的交叉比:$$r(xy, z_+ z_-) = \frac{(x – z_+)(y – z_-)}{(x – z_-)(y – z_+)}.$$给定Caley-Klein度量矩阵$\Psi$, 考虑如下矩阵群:$$G(\Psi) = \{ G \in R^{(n + 1) \times (n + 1)} | G^{-T} \Psi G^{-1} = \Psi \}.$$对于任意矩阵$G = (g_{ij}) \in G(\Psi)$, 可以定义如下一个分式线性变换$x’ = g(x)$:
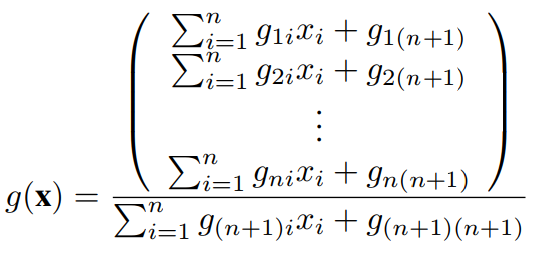
可以证明二次曲面$\Omega = \{ x | \psi(x, x) = 0 \}$在上述分式线性变换下是不变的, 即$$\psi(x, x) = 0 \Leftrightarrow \psi(g(x), g(x)) = 0, \forall G \in G(\Psi).$$由于分式线性变换能够保持交叉比不变, 结合命题1, 我们可以知道$$\forall x, y \in R^n(B^n), \rho(g(x), g(y)) = \rho(x, y), \forall G \in G(\Psi).$$因此, Caley-Klein度量是变换群$G(\Psi)$的不变量.
命题2 对于任意$G \in G(\Psi)$, 存在一个$(n + 1)$维反对称矩阵$W$满足$$G = (\Psi + W)^{-1}(\Psi – W).$$因此, 变换群$G(\Psi)$主要是由$n(n + 1)/2$个参数决定的.
通过使用分式线性变换, 与上述关于Caley-Klein度量的不变量的命题, 我们可以简化Caley-Klein度量的计算. 且对于计算过程中涉及到的三维矩阵与三维向量的乘法运算, 我们可以利用图形硬件将计算性能进行进一步地提升.