好像挺久没有在家里过过周末了, 尽管上上周人在家里, 但由于基本卧病在床, 所以基本没有周末宅家的感觉…… 所以说, 身体才是革命的本钱呐囧~ 复迭空间的基本群这一节内容也算是学了挺久了, 本文主要用于记录学习这一节内容的过程中碰到的一些疑惑点的解答.
参考材料
1. Induced map between fundamental groups from covering map is injective
2. Exam I Solutions
1. 书上P237命题5.3.1的证明中, 构造了一个从$a^\uparrow$出发的伦移$H^\uparrow$, 其在$t$时刻的切片为道路$(h^\uparrow)_t$. 当$t$变化时, $(h^\uparrow)_t$的起点始终只能在同一根纤维中移动, 因此只能始终固定不动. 这是因为, 伦移$H^\uparrow$是一个关于时刻$t$的连续函数, $a(0)$在复迭映射下的原像包含可能不止一个元素. 此时, 若$(h^\uparrow)_t$的起点在同一根纤维中的不同点之间移动, 而纤维都是离散空间, 这将与伦移$H^\uparrow$是一个关于时刻$t$的连续函数的事实矛盾.
2. 设$p: E \to B$是复迭映射, 则$\forall e \in E$,$$p_\pi : \pi_1(E, e) \to \pi_1(B, p(e))$$是单同态.
$\\$ 证: 记$c_e$为$e$的点道路, $c_{p(e)}$为$p(e)$的点道路, 问题即要证$ker \ p_\pi = $$ [c_e] \Leftrightarrow $使得$p_\pi([a]) = [c_{p(e)}]$成立的$[a]$仅有$[c_e]$.
$\\$ 回顾一下复迭映射的同伦提升性质: 设$p: E \to B$是复迭映射. 设$F $$ : X \times [0, $$ 1] \to B$是从$f: X \to B$开始的伦移, 而$f^\uparrow : $$ X \to E$是$f$关于$p$的提升, 则存在唯一一个从$f^\uparrow$开始的伦移$F^\uparrow : X \times [0, 1] $$ \to E$, 使得$F^\uparrow$是$F$关于$p$的提升.
$\\$ 不妨令$X = I$, $f^\uparrow_0$是$E$中的一条道路, 其在复迭映射$p$下的像$p \circ f^\uparrow_0 $$ = f_0$是$\pi_1( $$ B, p(e))$中的零伦映射, 则我们可得一个从道路$f_0$开始, 到一条点道路$f_1$结束的伦移$F$. 根据复迭映射的同伦提升性质, 我们可得一个从道路$f^\uparrow_0$开始, 到点道路$f_1$的提升结束的伦移$F^\uparrow$. 又由伦移$F^\uparrow$的唯一性, $B$中的点道路$f_1$的提升是唯一的, 故点道路$f_1$的提升亦为$E$中的点道路, 从而道路$f^\uparrow_0$亦为零伦映射, 命题得证.
3. 书上P238例1的证明中, 指出当$n \ge 2$时, 圆上镶嵌(即一点并) $n – 1$个小圆后得到的空间是$S^1 \vee S^1$的复迭空间, 即$n$个圆的一点并是2个圆的一点并的复迭空间. 事实上, 这在上一篇文章中已经提及, 只不过上一篇文章中未列出相应的多边形表示, 补充如下.
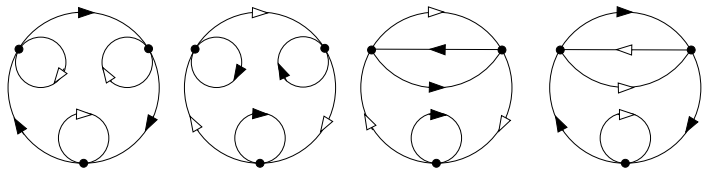
4. 设$p: E \to B$为一复迭映射,
$\\$ (1) 道路的提升的逆等于道路的逆的提升, 即对于底空间$B$中的任意道路$a$, 均有$(a^\uparrow)^{-1} = (a^{-1})^\uparrow$.
$\\$ 证: 首先取任意$t \in [0, 1]$, 由逆道路的定义有$a^{-1}(t) = a(1 – t)$, $( $$ a^\uparrow)^{-1}(t) = $$ a^\uparrow(1 – t)$. 又$a^\uparrow$为$a$关于$p$的提升, 故存在映射$f$(需要保证连续性?) 使得$$a^\uparrow = f \circ a, \\ (a^{-1})^\uparrow = f \circ a^{-1}.$$从而我们有$$(a^\uparrow)^{-1}(t) = a^\uparrow(1 – t) = (f \circ a)(1 – t) = \\ f \circ a(1 – t) = f \circ a^{-1}(t) = (a^{-1})^\uparrow(t).$$故命题得证.
$\\$ (2) 对于底空间$B$中的任意道路$a, b$, 道路$a$的终点为道路$b$的起点(即道路乘积$ab$是有意义的), 均有$a^\uparrow b^\uparrow = (ab)^\uparrow$.
证: 由于$a^\uparrow, b^\uparrow$分别为$a, b$关于$p$的提升, 且道路$a$的终点为道路$b$的起点, 故存在映射$f$使得$a^\uparrow = f \circ a$, $b^\uparrow = f \circ b$, 从而$$a^\uparrow b^\uparrow = (f \circ a)(f \circ b) = f \circ (ab) = (ab)^\uparrow.$$故命题得证.
5. 在泛复迭空间的情形, $\pi_1(B, b)$的元素和$p^{-1}(b)$的元素一一对应.
$\\$ 证: 由书上P240定理5.3.1可知, $H_e$在$\pi_1(B, b)$中的右陪集和$p^{-1}(b)$的元素一一对应. 当$E$为一个泛复迭空间时, 由$H_e$定义$H_e := p_\pi( $$ \pi_1(E, e))$可知$H_e$为一个平凡群($\pi_1(E, e)$为一个平凡群, $p_\pi$为一个单同态), 故$H_e$在$\pi_1(B, b)$中的右陪集与$\pi_1(B, b)$的元素一一对应, 命题得证.
6. 设$p: E \to B$是泛复迭映射. 证明任取$b \in B$, 存在$b$的邻域$U$, 使得包含映射诱导的基本群同态$i_\pi : \pi_1(U) \to \pi_1(B)$是平凡同态.
$\\$ 证: 取一个均匀复迭邻域$U$, 然后取$i: U \hookrightarrow B$的一个提升$i^\uparrow : U $$ \to E$, 则$i_\pi $$ = p_\pi \circ (i^\uparrow)_\pi$, 而$E$单连通时其基本群为一个平凡群, 故$(i^\uparrow)_\pi$是平凡同态, 从而$i_\pi$是平凡同态.
7. 设$a: [0, 1] \to S^1$是一条圈数为$n$的闭道路. 证明任取$x \in S^1$, $a^{-1}(x)$至少包含$n$个点.
$\\$ 证: 设$p: E^1 \to S^1, t \mapsto (cos(2\pi t), sin(2\pi t))$是泛复迭映射. 取$a$的提升$a^\uparrow$, 则由$a = p \circ a^\uparrow$可知$a^{-1} = (a^\uparrow)^{-1} \circ p^{-1}$. 又对于泛复迭空间$E^1$, $\pi_1(S^1, x)$的元素与$p^{-1}(x)$的元素一一对应.
$\\$ $\because a$是一条圈数为$n$的闭道路, 故$\pi_1(S^1, x)$的元素数量至少为$n$, 从而$p^{-1}(x)$的元素数量至少为$n$. 在$(a^\uparrow)^{-1}$的复合作用下, $a^{-1}(x)$的元素数量亦至少为$n$, 命题得证.