结束了中秋假期与长沙之旅, 又迎来了一个宅家的周末~ 这次中秋假期带女朋友回家见了见爸妈, 感觉还不错嘿嘿~ 而后便来了一场长沙之旅, 说实话, 旅游一天比”搬砖” 一天辛苦多了QAQ…… 话不多说, 进入正题, 本文用以结束泛复迭空间的存在性一节内容的学习.
参考材料
1. locally simply-connected vs. semilocally simply-connected
2. Wedge sum of circles and the Hawaiian Earring
3. The fundamental group of the earring space
4. Hawaiian earring space
5. 连续的一一映射,其逆映射怎样才连续?
6. Show that a set that is open in the subspace topology is open in the full space topology.
7. P50 (49)万有覆盖之构造
1. 若拓扑空间$X$半局部单连通, 则下述定义等价:
(1) 如果拓扑空间$X$中的每个点存在道路连通邻域$U$, 使得包含映射$i: U \hookrightarrow X$诱导的基本群的同态$i_\pi : \pi_1(U, x) \to \pi_1(X, x)$是平凡同态, 则称$X$半局部单连通.
(2) 如果拓扑空间$X$中的每个点存在道路连通邻域$U$, 使得道路连通邻域$U$中的闭道路都在$X$中(注意, 此处黑体强调的部分亦是与局部单连通性质最大的区别所在) 零伦, 则称$X$半局部单连通.
$\\$ 证: (1) $\to$ (2): 由包含映射的定义可知, 存在收缩映射$r : X \to U$使得$r_\pi \circ i_\pi $$ = id_\pi$成立. 由于$id_\pi$为一个同构, 故$i_\pi$为一个单同态, 即当闭道路$a$与闭道路$b$不同伦时, $i_\pi(\left \langle a \right \rangle) \ne i_\pi(\left \langle b \right \rangle)$. 又$i_\pi$为一个平凡同态, 故所有的闭道路类在$i_\pi$的作用下均变换为一个点道路类$\left \langle e_x \right \rangle$, 且$i_\pi(\left \langle e_x \right \rangle) $$ = \left \langle e_x \right \rangle$, 从而所有的闭道路都与点道路$e_x$同伦.
$\\$ (2) $\to$ (1): 由于道路连通邻域$U$中的闭道路$a$都零伦, 且$i_\pi(\left \langle e_x \right \rangle) = $$ \left \langle e_x \right \rangle$, 则$i_\pi( $$ \left \langle a \right \rangle) = \left \langle e_x \right \rangle$, 从而说明$i_\pi$为一个平凡同态.
$\\$ 综上所述, 命题得证.
2. 流形以及有限单纯复形都是半局部单连通的.
$\\$ 证: 由流形的定义可知, 流形$X$中的每一点$x$都有一个开邻域$U$与欧氏空间同胚, 而欧氏空间是一个单连通空间, 那么这个邻域一定道路连通并且基本群平凡. 因此, 流形都是半局部单连通的.
$\\$ 同理, 由有限单纯复形的定义可知, 其中每个单形均为欧氏空间中的一个子集, 由上述论述可知, 有限单纯复形亦都是半局部单连通的.
3. 夏威夷耳环$X$不半局部单连通, 而可数无穷多个圆周的一点并$Y $$ = \bigvee_{n = 1}^{\infty} S^1$半局部单连通.
$\\$ 证: 虽然两个空间看上去很像, 但由于两者拓扑结构的不同, 导致两者的半局部单连通性质不一致, 而这也是证明中最为关键的一点.
$\\$ 夏威夷耳环$X$的拓扑是关于二维欧氏空间$E^2$的子空间拓扑, 则在$X$中坐标原点$O = (0, 0)$的任何邻域内都包含一个不零伦的小圆(圆周$S^1$的基本群非平凡), 所以它不半局部单连通.
$\\$ 可数无穷多个圆周的一点并$Y$的拓扑是在商集合$\bigcup_{n =1 }^{\infty} S^1 / \sim$上的商拓扑, 其中, $\sim$为$\bigcup_{n =1 }^{\infty} S^1$上的等价关系, 表示可数无穷多个圆周的交点均为等价的.在商拓扑下, $Y$中的开集即为$\bigcup_{n =1 }^{\infty} S^1$中的开集, 故在$Y$中任取一点$y$, 其开邻域总是由其所在的圆周中的开集构成的(圆周$S^1$是与一维欧氏空间$E^1$的一点紧化同胚的, 故此处圆周$S^1$上的拓扑是由一维欧氏空间$E^1$的拓扑得到的), 如下图所示.
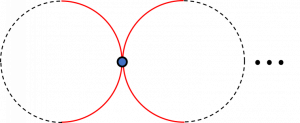
4. 注意, 如果$X$局部道路连通, 则我们可以在$x$的任何一个邻域$U$内取一个更小的道路连通开邻域$V$. 也就是说, 局部道路连通并且半局部单连通空间$X$中的每个点$x$存在道路连通的开邻域$U$(注意, 重点是”开”), 使得包含映射$i: A \hookrightarrow X$诱导的基本群的同态$i_\pi : \pi_1(A, $$ x) \to \pi_1(X, x)$是平凡同态.
5. 书上P245的证明中定义了一个一一对应$p_\alpha : U_\alpha \to V_x$, $\gamma \mapsto p( $$ \gamma)$, 因此可以在$U_\alpha$上定义一个拓扑$\tau_\alpha$如下:$$\tau_\alpha = \{ A \subseteq U_\alpha | p(A) \subseteq B, p(A) \ is \ open. \},$$使得$p_\alpha$变成同胚.
$\\$ 证: 首先证明$p_\alpha = p | _{U_\alpha}$为一个单射, 对于$\forall \alpha w_1, \alpha w_2 \in U_\alpha$, 其中, $w_1$, $w_2$均为$V_x$中起点为$x$的道路在$B$中的道路类. 若$p_\alpha(\alpha w_1) = $$ p_\alpha( $$ \alpha w_2)$, 则由$p_\alpha$定义有$w_1$与 $w_2$的终点相同. 又由半局部单连通的定义可知$w_1(w_2)^{-1}$在$B$中零伦, 即$w_1$与$w_2$在$B$中定端同伦, 从而$\alpha w_1 = $$ \alpha w_2$.
$\\$ 接下来证明$p_\alpha$为一个满射, 这是显然的, 因为对于$\forall y \in V_x$, 在$B$中总存在从$x$到$y$的道路, 这亦是由$B$的道路连通性保证的.
$\\$ 最后, 我们来证明$p_\alpha$为一个同胚, 我们需要从两方面进行证明. 任取$U_\alpha$中的开集$U$, 则$U$在$p_\alpha^{-1}$下的原像$p(U)$亦为一个开集, 这是由$\tau_\alpha$的定义所决定的.
$\\$ 另外一方面, 任取$V_x$中的开集$V$, 则该开集亦为底空间$B$中的开集, 这是因为由子空间拓扑的定义, $V = V_x \cap U$, 其中$U$为$B$中的开集. 因为$U$与$V_x$在底空间$B$上都是开的, 并且有限个开集的交集依旧为一个开集, 故$V$在底空间$B$中亦为一个开集. 这样一来, $V$在$p_\alpha$下的原像$p_\alpha^{-1}( $$ V) \subseteq U_\alpha$亦为一个开集, 否则由$\tau_\alpha$的定义知$p_\alpha^{-1}(V) \notin $$ \tau_\alpha$($p(p_\alpha^{-1}(V) $$ ) = $$ V$为底空间$B$中的开集), 这是矛盾的.
$\\$ 综上所述, $p_\alpha$为一个连续的一一对应, 且其逆映射亦为连续的, 故$p_\alpha$为一个同胚.
6. 书上P245在对于$\Omega_b$道路连通的证明中任取一条从$b$出发的道路$w: $$ [0, 1] \to $$ B$, 定义道路$w_s : [0, 1] \to B$, $w_s(t) = w(st)$, 则$$w^\uparrow : [0, 1] \to \Omega_b, t \mapsto \left \langle w_t \right \rangle$$就是一条从$\left \langle w \right \rangle$到以$b$为基点的点道路类$\left \langle e_b \right \rangle$的道路.
$\\$ 证: 仅需证明$w^\uparrow$为一个连续映射即可. $\Leftrightarrow$ 任取道路类$\alpha \in \Omega_b$, $(w^\uparrow $$ )^{-1} (U_\alpha)$为$[0, 1]$中一个开集. $\Leftrightarrow$ 任取$s_0 \in (w^\uparrow)^{-1}(U_\alpha)$, 存在$s_0$的一个开邻域包含于$(w^\uparrow $$ )^{-1}(U_\alpha)$中.
$\\$ 由于$s_0 \in (w^\uparrow)^{-1}(U_\alpha)$, i.e. $\left \langle w_{s_0} \right \rangle = w^\uparrow(s_0) \in U_\alpha$, i.e. 存在一个$V_x$中起点为$x$的道路在$B$中的道路类$\beta$, s.t. $\left \langle w_{s_0} \right \rangle = \left \langle \alpha \beta \right \rangle$, $\Rightarrow$ $w( $$ s_0) = \beta(1) \in V_x$, $\Rightarrow$ $s_0 $$ \in w^{-1}(V_x) \subseteq [0, 1]$. 又$V_x$为一个开集, $w$为一个连续映射, 故$w^{-1}(V_x)$亦为一个开集. 接下来我们仅需证明$w^{-1}(V_x) $$ \subseteq (w^\uparrow)^{-1}(U_\alpha)$即可.
$\\$ 对于$\forall s \in w^{-1}(V_x)$, $\left \langle w_s \right \rangle = w^\uparrow(s) \in U_\alpha$. 已知$\left \langle w_{s_0} \right \rangle = \left \langle \alpha \beta \right \rangle$, 则存在一个$V_x$中起点为$x$的道路在$B$中的道路类$\delta_s$, s.t.$$\left \langle w_s \right \rangle = \left \langle w_{s_0} \delta_s \right \rangle = \left \langle \alpha \beta \delta_s \right \rangle = \left \langle \alpha (\beta \delta_s) \right \rangle \in U_\alpha.$$综上所述, 命题得证.
7. 书上P244定理5.4.1之所以要求底空间$B$道路连通并且局部道路连通, 是因为道路连通与局部道路连通这两个性质并不具备相互包含的关系, 存在道路连通但不局部道路连通的拓扑空间: Topologist’s sine curve.
8. 书上P244定理5.4.1的证明过程可提炼为三步:
$\\$ (1) 考虑从基点$b \in B$出发的所有道路类构成的集合$\Omega_b$, 为其定义一个拓扑. (私以为这亦是整个证明过程中最漂亮的一步~)
$\\$ (2) 证明$p: \Omega_b \to B$是个复迭映射.
$\\$ (3) 证明$\Omega_b$单连通.