最近三周的周末都是在宅家, 目前其实处于有点小迷茫的状态, 在学完代数拓扑以后又暂时不大想开新的大坑. 恰巧最近发现一个宝藏视频合集: 徐鹏程老师的计算拓扑系列, 目前该系列的视频数量不多(貌似已经停止更新了…… 有点可惜QAQ), 而且老师对知识点的讲解非常详细清晰, 适合入门, 于是便看完了这个视频合集, 并以本文记录下与同调群的计算相关的知识点(持续同调目前主要用于点云数据分析, 故暂不涉及).
参考材料
1. 计算拓扑
2. Benjamin A. Burton, Ryan Budney, William Pettersson, et al., Regina: Software for low-dimensional topology, http://regina-normal.github.io/, 1999–2022.
3. P57 (56)单纯同调计算举例
4. PC3-4_solution
5. Smith 标准型与同调群的一般计算
6. Calculating Homology of a Simplicial Complex Using Smith Normal Form
7. Homology of Möbius Strip
可三角剖分空间的同调群可以通过代表边缘同态的矩阵来计算. 它的既约版本提供了闭链群和边缘链群的秩, 而两者的差就给出了Betti数. 此外, 下文中对于同调群的计算, 均是在域$\mathbb{Z}_2$(模2整数加法群, 一般又记为$\mathbb{Z} / 2\mathbb{Z}$) 中进行的. 意即, 我们只考虑所有系数都是模2整数的$n$维链(形式线性组合), 此时, 所有的$n$维链并不构成线性空间, 而只是构成一个交换群$C_n(K ; \mathbb{Z}_2)$. 整系数的$n$维闭链构成它的一个子群$Z_n(K ; \mathbb{Z}_2 $$ )$, 而整系数$n$维边缘链进一步构成这个子群里的一个子群$B_n( $$ K ; \mathbb{Z}_2)$. 交换群的子群都是正规子群, 因此可以作商群. 复形$K$的$n$维整系数同调群的定义$$H_n(K ; \mathbb{Z}_2) = Z_n(K ; \mathbb{Z}_2) / B_n(K ; \mathbb{Z}_2) = Ker \partial_n / Im \partial_{n + 1}$$也由此而来. 需要注意的是, 本文讨论的同调群的计算均是在可三角剖分空间中进行的; 此时, 我们通常不对拓扑空间的同调群与其对应的单纯复形的同调群加以区分, 这是由书上P152定理3.6.1所保证的.
Betti数是拓扑不变量, 即如果拓扑空间$M$有两个有限单纯剖分$K_1$, $K_2$, 则$b_n(K_1) = b_n(K_2)$.
此外, 我们将$n$个$\mathbb{Z}$的直和简记为$\mathbb{Z}^n$, 下文不再赘述.
1. 欧拉-庞加莱公式
单纯复形的欧拉特征数是所有维度的单形的数量的交错和. 类似的, 第$p$个同调群的秩等于第$p$个闭链群的秩减去第$p$个边缘链群的秩. 记$n_p = rank C_p(K)$, $z_p $$ = rank Z_p = dim(Ker \partial_p)$, $b_p = rank $$ B_p(K) = dim(Im \partial_{p + 1})$, 则有$$n_p = z_p + b_{p – 1}.$$这个是线性代数里面的定理, 任何线性映射$f: U \to V$, $U$的维度等于$f$的核的维度加上$f$的像的维度. 欧拉特征数是$n_p$的交错和, 所以$$\sum_{p \ge 0} (-1)^p(z_p + b_{p – 1}) = \sum_{p \ge 0} (z_p – b_p).$$(欧拉-庞加莱定理) 一个拓扑空间的欧拉特征数是Betti数的交错和, 即$$\chi = \sum_{p \ge 0} (-1)^p \beta_p,$$其中, $\beta_p = z_p – b_p = n_p – b_{p – 1} – b_p$. 以上公式又称欧拉-庞加莱公式(Euler-Poincare Formula).
2. 边缘矩阵
为了计算同调群, 我们需要从两个地方整合信息, 一是闭链群, 二是边缘链群. 假设$K$是一个单纯复形. 它的第$p$个边缘矩阵是以$p – 1$维单形为行, $p$维单形为列. 任意选定单形的顺序(即选定定向), 对于每个维度, 该矩阵为$\partial_p = [a^j_i]$, $i$的取值从1到$n_p$, 如果第$i$个$p – 1$维单形是第$j$个$p$维单形的一个面, 则令$a^j_i = 1$, 否则令$a^j_i = 0$. 给定一个$p$维链$c = \sum a_i \sigma_i$, 我们有$$\partial_p c = \begin{bmatrix}
a^1_1 & a^2_1 & \cdots & a^{n_p}_1 \\
a^1_2 & a^2_2 & \cdots & a^{n_p}_2 \\
\vdots & \vdots & \ddots & \vdots \\
a^1_{n_{p – 1}} & a^2_{n_{p – 1}} & \cdots & a^{n_p}_{n_{p – 1}}
\end{bmatrix}\begin{bmatrix}
a_1 \\
a_2 \\
\vdots \\
a_{n_p}
\end{bmatrix}.$$总的来说, 列的集合表示一个$p$维链, 这些列的求和给出了它的边缘. 同理, 行的集合代表了一个$p – 1$维链, 这些行的求和给出了它的上边缘(Coboundary).
3. Smith标准型
使用初等变换, 我们可以将第$p$个边缘矩阵化简为Smith标准型(Smith Normal Form), 也就是说除了对角线上的元素是1以外其它都是0(对角线上的元素也不全为1, 但前$k$个要为1). 由于$n_p = rank $$ C_p(K)$是第$p$个边缘矩阵的列的数量, $n_p = b_{p – 1} + z_p$, 所以最左边的$b_{p – 1}$个列的对角线元素为1, 最右边的$z_p$个列全为0. 前者代表非0边缘生成了$p – 1$维边缘链群的$p$维链, 后者则代表了生成$Z_p(K)$的$p$维闭链. 只要将所有的边缘矩阵都化为标准型, 我们就可以得到Betti数$\beta_p = $$ rank Z_p(K) – rank B_p(K)$. 要得到边缘链群和闭链群的基底, 我们可以追踪代表行运算和列运算的矩阵的乘积. 记$U_{p – 1}$为左乘积, $V_p$为右乘积, 我们得到标准型如下: $$N_p = U_{p – 1} \partial_p V_p,$$则闭链群的新基底由$V_p$的最后$z_p$个列给出. 类似地, 边缘链群的基底则由$U_{p – 1}$的前$b_{p – 1}$个列给出.
4. 过滤和配对
定义1(过滤) 一个$n$维单纯复形${\textstyle \sum}$的过滤是一系列嵌套的复形:$$\emptyset = {\textstyle \sum_{-1}} \subset {\textstyle \sum_{0}} \subset {\textstyle \sum_{1}} \subset \cdots \subset {\textstyle \sum_{n}} = {\textstyle \sum}.$$包含映射$$f: {\textstyle \sum_{i- 1}} \hookrightarrow {\textstyle \sum_{i}}, \\ f(p) = p$$诱导了下同调群之间的同态$f_* : H_k(\textstyle \sum_{i – 1}) \to H_k(\textstyle \sum_{i})$. 复形间的嵌套序列对应了同调群的序列$$ 0 = H_k(\textstyle \sum_{-1}) \to H_k(\textstyle \sum_{0}) \to \cdots \to H_k(\textstyle \sum_{n}) = H_k(\textstyle \sum).$$我们将${\textstyle \sum}$的所有单纯形依照维数升序排列$$\sigma_1, \sigma_2, \cdots, \sigma_{n – 1}, \sigma_n,$$每一次添加一个$k$维单纯形, 有两种情况可能发生. 第一种情况, $\sigma_i$生成一个$k$维非边界闭链$c_k$, 同调群的$k$维Betti数$\beta_k$加1, 这时我们称$\sigma_i$为正的单形; 第二种情况, $\sigma_i$消灭掉一个$k – 1$维已经存在的闭链$c_{k – 1}$, 同调群的$k – 1$维Betti数$\beta_{k – 1}$减1, 这时我们称$\sigma_i$为负的单形.
定义2(配对) 在上述过滤中, $\sigma_i$是一个负单形, 消灭了$k – 1$维已经存在的闭链$c_{k – 1}$, 我们将被消灭掉的闭链$c_{k – 1}$中最后一个正单形和$\sigma_i$配对.
过滤和配对提供了另外一种计算出各阶Betti数的思路, 我们进而可以计算出各阶同调群, 具体计算过程可参考徐鹏程老师的视频(详见参考材料1视频合集中的计算拓扑05, 计算拓扑06).
5. 相关例子
例1 计算下图表示的有限单纯复形$K$的各阶同调群.

解: 由于有限单纯复形$K$含4个点, 4条边, 故$$C_0(K) \cong \mathbb{Z}^4, n_0 = 4, \\ C_1(K) \cong \mathbb{Z}^4, n_1 = 4.$$从而, 我们有$\partial_1(e_1) = v_2 – v_1$(在域$\mathbb{Z}$中进行计算, 若在域$\mathbb{Z}_2$中进行计算, 则其结果为$v_2 + v_1$), 同理可得$$\partial_1(e_2) = v_1 – v_3, \\ \partial_1(e_3) = v_3 – v_2, \\ \partial_1(e_4) = v_4 – v_3.$$又$\partial_1(e_1 + e_2 + e_3) = 0$, $Ker \partial_1 \cong \mathbb{Z}$, $$Im \partial_1 = \left \langle v_2 – v_1, v_1 – v_3, v_3 – v_2, v_4 – v_3 \right \rangle \\ = \left \langle v_2 – v_1, v_1 – v_3, v_4 – v_3 \right \rangle \cong \mathbb{Z}^3,$$从而$z_1 = 1$, $b_0 = 3$. 从直观上来讲, 我们需要”取走” $z_1$条边(如$e_1$) 才能破圈(即得到一棵最小生成树), 除去公共点(如$v_3$), 剩下$b_0$条边(如$e_2, e_3$与$e_4$) 恰好对应$b_0$个0维单形(如$v_1, v_2$与$v_4$).
例2 计算下图表示的有限单纯复形$K$的各阶同调群.

解: 先计算$Z_1(K)$: 由于$$\partial_1(e_1 + e_2 + e_3) = v_0 – v_2 + v_1 – v_0 + v_2 – v_1 = 0,$$故$e_1 + e_2 + e_3 \in Z_1(K)$. 又$\partial_1(e_4 + e_5 – e_3) = 0$, 故$e_4 + e_5 – $$ e_3 \in $$ Z_1(K)$.
$\\$ 不妨取$\forall c \in C_1(K)$, 则$c = \sum^5_{i = 1} n_i e_i$, 从而$c \in Z_1(K)$, $\Leftrightarrow \partial_1 c $$ = 0$, $\Leftrightarrow $$ \left\{\begin{matrix}
n_1 = n_2 = n, \\
n_4 = n_5 = m,
\end{matrix}\right.$$c$必长成$n(e_1 + e_2) + n_3 e_3 + m(e_4 $$ + e_5)$的形式, $\Leftrightarrow $$ \partial_1 c$中$v_1$前系数为0, $v_2$前系数为0, i.e. $$\left\{\begin{matrix}
n – n_3 – m = 0, \\
-n + n_3 + m = 0.
\end{matrix}\right.$$因此, $\partial_1 c = 0$, $\Leftrightarrow n – n_3 – m = 0$, i.e. $n = m + n_3$,$$c = (m + n_3)(e_1 + e_2) + n_3 e_3 + m(e_4 + e_5) \\ = (m + n_3)(e_1 + e_2 + e_3) + m(e_4 + e_5 – e_3).$$因而, $Z_1(K) = \mathbb{Z}(e_1 + e_2 + e_3) + \mathbb{Z}(e_4 + e_5 – e_3)$.
$\\$ 接下来计算$B_1(K) = Im(C_2(K) \overset{\partial_2}{\longrightarrow} C_1(K))$: 由于$C_2(K) = $$ \mathbb{Z}\sigma$, 故$B_1(K) = \mathbb{Z}(\partial_2 \sigma) = \mathbb{Z}(e_4 + e_5 – e_3)$, 从而$$H_1(K) = Z_1(K) / B_1(K) \cong \mathbb{Z}.$$同理可得, $H_2(K) = Z_2(K) / B_2(K) = Z_2(K) = 0$, $H_0(K) \cong $$ \mathbb{Z}$.
例3 考虑$K$为环面. 已知$H_0(K ; \mathbb{Z}_2) \cong \mathbb{Z}_2$, $H_1(K ; \mathbb{Z}_2) \cong \mathbb{Z}_2^2$, $H_2 $$ (K ; \mathbb{Z}_2) = $$ \mathbb{Z}_2$. 所以$\beta_0(K) = 1$, $\beta_1(K) = 2$, $\beta_2(K) = 1$. 如下图所示. 容易算出$$C_0(K) = \left \langle v \right \rangle \cong \mathbb{Z}_2, \\ C_1(K) = \left \langle a, b, c \right \rangle \cong \mathbb{Z}_2^3, \\ C_2(K) = \left \langle A, B \right \rangle \cong \mathbb{Z}_2^2.$$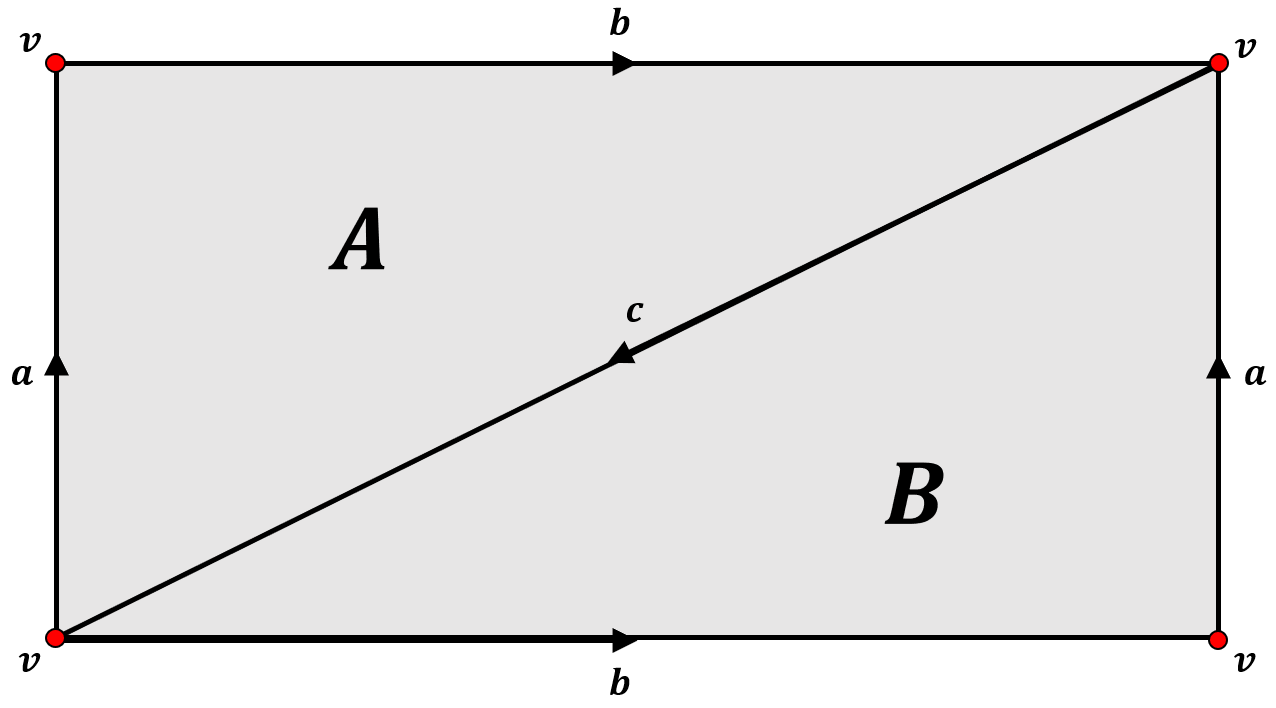
所以$n_0 = 1$, $n_1 = 3$, $n_2 = 2$. 可以得到$D_1 = (0 \ 0 \ 0)$, 元素为0是因为这个矩阵也是$mod \ 2$的, 只有一个顶点$v$, 边$a$的两个顶点$v$, 所以元素为$2 \equiv 0(mod \ 2)$. 也就是说, $rank D_1 = 0$. 补充定义$rank $$ D_0 = rank D_3 = 0$.$$D_2 = \begin{pmatrix}
1 & 1 \\
1 & 1 \\
1 & 1
\end{pmatrix} \xrightarrow{r_1 + r_2, r_1 + r_3} \begin{pmatrix}
1 & 1 \\
0 & 0 \\
0 & 0
\end{pmatrix} \xrightarrow{c_1 + c_2} \begin{pmatrix}
1 & 0 \\
0 & 0 \\
0 & 0
\end{pmatrix},$$所以$rank D_2 = 1$. 根据公式, $$\beta_0 = n_0 – rank D_0 – rank D_1 \\ = 1 – 0 – 0 = 1, \\ \beta_1 = 3 – 0 – 1 = 2, \\ \beta_2 = 2 – 1 – 0 = 1.$$
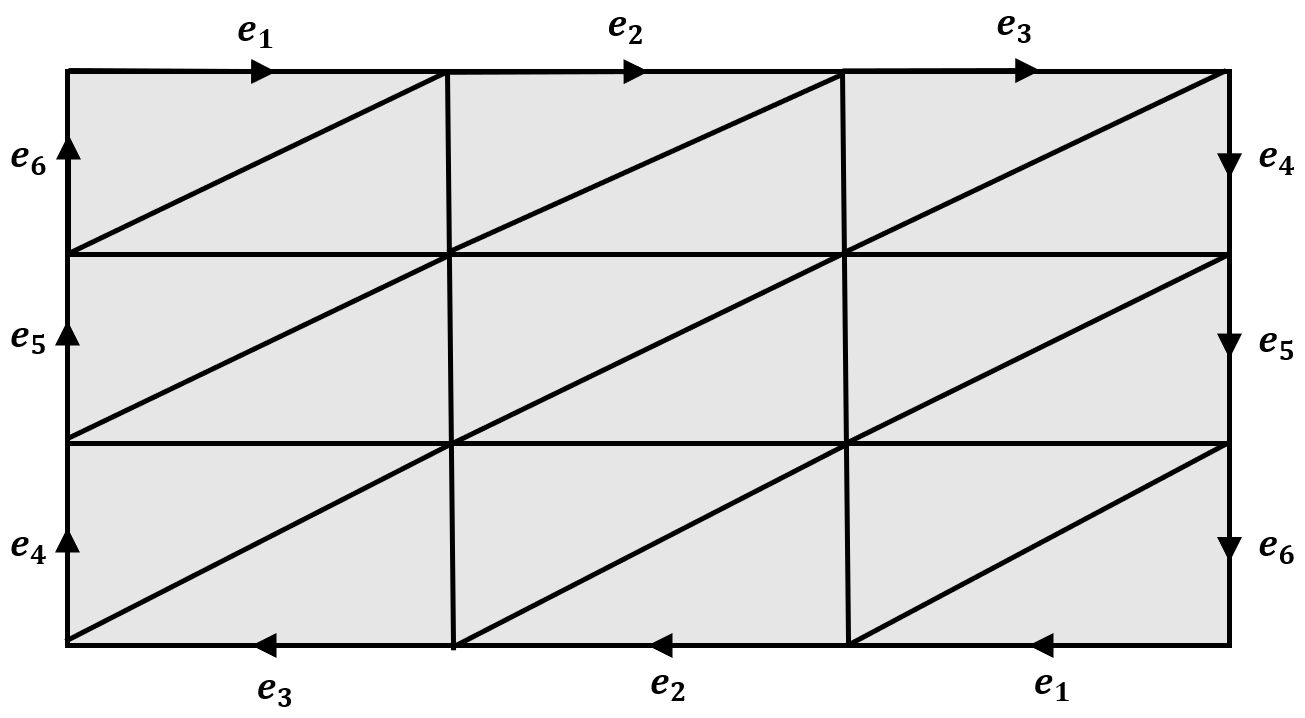
例4 计算射影平面$RP^2$的各阶同调群.
$\\$ 解: 射影平面$RP^2$的多边形表示的三角剖分如下图所示.
其各阶同调群的具体计算过程可参考庄晓波老师的视频(详见参考材料3), 在视频中庄晓波老师使用了Push to the Boundary的方法, 计算过程十分有意思~
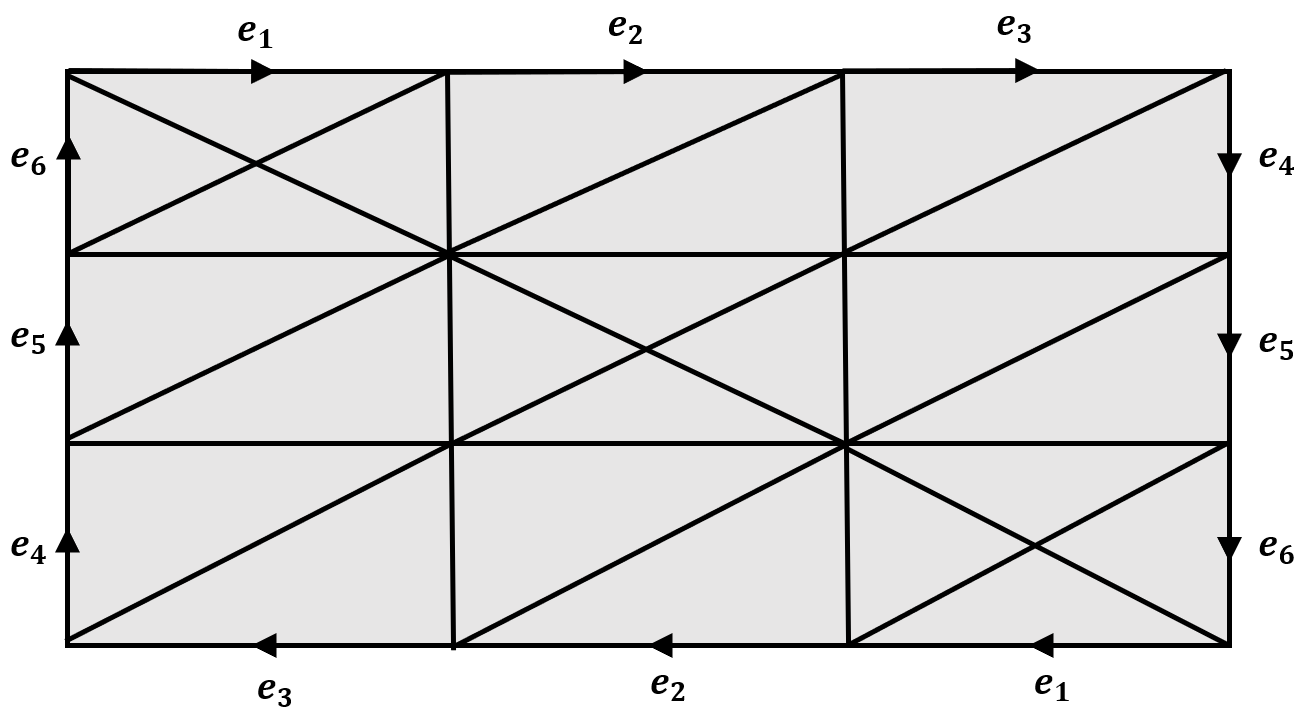
$\\$ 需要注意的是, 下图所示的三角剖分并不能成为射影平面$RP^2$的多边形表示的三角剖分.