不出意外地, 自己于上周六进化成了一个小阳人, 并已居家办公了一周. 一周以来, 虽然免去了通勤的痛苦, 但身体上的病痛与需要自己觅食的难处也让自己Emo了不少. 目前, 身体状态已经恢复了不少了, 故趁这几天工作节奏比较轻松的时候, 记录一下切线空间法线贴图的相关知识点.
参考材料
1. Lesson 6bis: tangent space normal mapping
2. 法线贴图
3. 切线空间(Tangent Space)完全解析
自己一开始是在learnopengl上了解到切线空间法线贴图的, 但其讲解一直让我云里雾里. 直到学习了tinyrenderer的第6节课, 自己才算真正地掌握了切线空间法线贴图.
1. 开篇
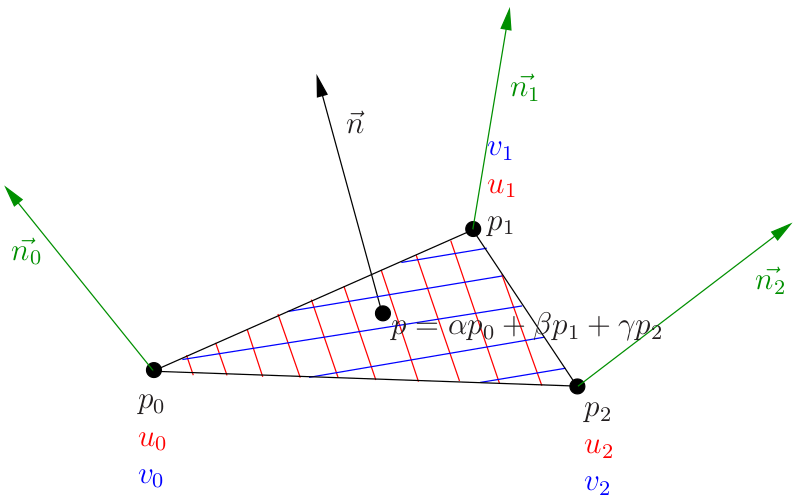
对于一个三角形的每个顶点, 我们已知其坐标$p$, 纹理坐标$uv$与法线. 对于待渲染的当前像素, 软光栅器给出了其重心坐标($\alpha, \beta, \gamma$). 这意味着三角形内任一点的坐标$p$均可以由$p = \alpha p_0 + \beta p_1 + \gamma p_2$得到. 同理可得:$$ u = \alpha u_0 + \beta u_1 + \gamma u_2, \\ v = \alpha v_0 + \beta v_1 + \gamma v_2, \\ \vec{n} = \alpha \vec{n}_0 + \beta \vec{n}_1 + \gamma \vec{n}_2.$$而以$UV$空间中的$U$轴与$V$轴为两个坐标轴, 即可构造出切线空间.
2. 如何从3个样本点重建一个3维线性函数
接下来, 我们的目标是要为待渲染的每个像素计算2个向量(分别为切向量与副切向量). 假设给定了一个定义在三角形$T$上的高度函数$f$, s.t. $$f(x, y, z) = Ax + By + Cz + D,$$其中, $\forall (x, y, z) \in T$. 尽管并不清楚$A, B, C$与$D$的值, 但可以准确知道高度函数$f$在三角形$T$上的三个顶点$p_0, p_1, p_2$上的取值:$$f(x, y, z) = Ax + By + Cz + D : \left\{\begin{matrix}
f(p_0) = f_0, \\
f(p_1) = f_1, \\
f(p_2) = f_2.
\end{matrix}\right.$$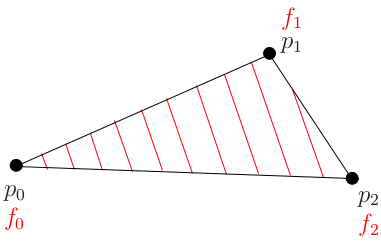
不妨把高度函数$f$想象成一个斜面的高度图, 如上图所示. 我们在平面上固定3个不同的(非共线的)点, 并且我们知道这些点的$f$值. 三角形内的红线分别表示对应于$f_0$, $f_0 + 1$, $f_0 + 2$等的等值线. 对于线性函数而言, 等值线是相互平行的.
$\\$ 实际上, 我们对垂直于等值线的方向更感兴趣. 若我们沿着等值线移动, 其高度值是不会发生改变的. 但如若我们稍微偏离了当前所在的等值线, 则其高度值亦会产生一些变化. 当我们沿着与等值线垂直的方向移动时, 则我们也得到了一个高度值变化最快的方向.
$\\$ 显然, 一个函数的值增加最快的方向便是其梯度方向. 对于一个线性函数$f(x, y, $$ z) = Ax + By + Cz + D$而言, 其梯度为一个常向量$(A, B, C)$. 由于我们并不知道$(A, B, C)$的值, 接下来我们便要从高度函数$f$的3个样本点出发, 推导出$A, B$与$C$的值.
$\\$ 我们已知3个点$p_0, p_1, p_2$与对应的3个高度值$f_0, f_1, f_2$. 我们需要找到高度函数$f$的梯度向量$(A, B, C)$. 不妨考虑另一个函数$g$, 其定义为$g(p) = f(p) – f(p_0)$.
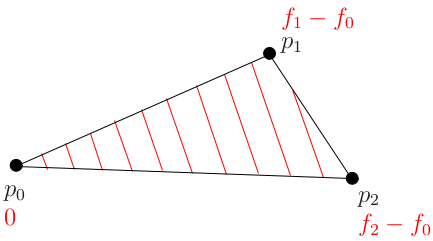
显然, 我们只是平移了斜面, 但并没有改变斜面的倾斜角,因此, 高度函数$f$和$g$的梯度方向是相同的. 接下来, 将高度函数$g$重定义如下:$$g(p) = f(p) – f(p_0) = (p^x \ p^y \ p^z \ 1) \begin{pmatrix}
A \\
B \\
C \\
D
\end{pmatrix} – (p^x_0 \ p^y_0 \ p^z_0 \ 1) \begin{pmatrix}
A \\
B \\
C \\
D
\end{pmatrix} \\ = \overrightarrow{p_0 p} \cdot (A \ B \ C).$$故高度函数$g$即为向量$p – p_0$与$(A, B, C)$的内积. 若从$p_0$变化至$p_2$, 则函数$g$会从0变化至$f_2 – f_0$. 换言之, 向量$p_2 – p_0$与$(A, B, C)$的内积为$f_2 – f_0$. 同理可得向量$p_1 – p_0$与$(A, B, C)$的内积为$f_1 – f_0$. 又$(A, B, C)$为一个梯度向量, 若设其法向为$\vec{n}$, 则其与梯度向量$(A, B $$ , C)$的内积为0:$$\left\{\begin{matrix}
\overrightarrow{p_0 p_1} \cdot (A \ B \ C) = f_1 – f_0, \\
\overrightarrow{p_0 p_2} \cdot (A \ B \ C) = f_2 – f_0, \\
\vec{n} \cdot (A \ B \ C) = 0.
\end{matrix}\right.$$将上式写为矩阵的形式:$$\begin{pmatrix}
(\overrightarrow{p_0 p_1})^x & (\overrightarrow{p_0 p_1})^y & (\overrightarrow{p_0 p_1})^z \\
(\overrightarrow{p_0 p_2})^x & (\overrightarrow{p_0 p_2})^y & (\overrightarrow{p_0 p_2})^z \\
(\vec{n})^x & (\vec{n})^y & (\vec{n})^z
\end{pmatrix}\begin{pmatrix}
A \\
B \\
C
\end{pmatrix} = \begin{pmatrix}
f_1 – f_0 \\
f_2 – f_0 \\
0
\end{pmatrix}.$$最终, 我们得到了一个简单的线性方程:$$M \vec{x} = \vec{b} \Rightarrow \vec{x} = M^{-1} \vec{b}.$$显然, 矩阵$M$与高度函数$f$并无关系, 它被三角形本身唯一确定.
3. 计算达布基并应用法向的摄动
达布基是一个三元组$(\vec{i}, \vec{j}, \vec{n})$, 其中, $\vec{n}$为经重心坐标插值得到的法向, $\vec{i}, \vec{j}$则可通过如下式子进行计算:$$\vec{i} = M^{-1} \begin{pmatrix}
u_1 – u_0 \\
u_2 – u_0 \\
0
\end{pmatrix}, \\ \vec{j} = M^{-1} \begin{pmatrix}
v_1 – v_0 \\
v_2 – v_0 \\
0
\end{pmatrix}.$$如此一来, 将$\vec{i}, \vec{j}$与法向$\vec{n}$列排得到的变换矩阵$M’$(又称TBN矩阵), 便可将切线空间中的向量变换至世界空间中.
$\\$ 需要注意的是, $p_i$通常取经透视除法后的屏幕坐标, 而法向$\vec{n}$所在的空间并无限制, 只要与光源的位置向量(相对于世界空间) 所在的空间保持一致即可. 如此一来, 后续进行的法向与光源的位置向量的内积运算才是有意义的.
4. 相关问题
对于规范的TBN矩阵而言, TB二轴与UV轴方向极大多数情况很可能并不相同. 当顶点法线在建模软件中被修改为不垂直于该面片时, TB平面甚至不在三角形面片上; 当UV经过拉伸时, 因TB二轴在正交化前与UV方向相同, 故正交化后TB二轴必然与UV方向是有所偏差的, 而对于一个多面片的模型UV展开, 这种拉伸旋转的情况简直司空见惯.
$\\$ 此外, TBN矩阵在VS中构建后, PS中经过插值了就不正交了, 一般来说应该重新正交化. 如果追求精度的话, TBN矩阵应当在PS中构建, 不过实测即便直接用插值后的矩阵也几乎没有什么差别, 毕竟法线微小点错了谁也看不出来, 所以性能权衡下Unity的URP管线就是直接用的未正交的插值矩阵.