这个周末应该是身为网易员工的最后一个周末了, 目前的心态好似早已丢掉了不安的部分, 只剩下对下周三离职的坦然, 与对新生活的期待~ 心之所向, 无惧无悔. 回到正题来, 本文主要用于记录一些关于光线追踪的知识点.
参考材料
1. 高级光照
1. 计算观察光线
为了生成光线, 我们首先需要一个关于光线的数学表达式. 实际上, 光线仅被一个原点与一个方向所决定, i.e. 从观察点$\mathbf{e}$出发, 经过像平面上点$\mathbf{s}$的三维光线为$$\mathbf{p}(t) = \mathbf{e} + t(\mathbf{s} – \mathbf{e}),$$则$\mathbf{s} – \mathbf{e}$为光线的方向. 上式可以解释为: 我们从观察点$\mathbf{e}$出发, 沿着向量$\mathbf{s} – \mathbf{e}$前进距离$t$到达点$\mathbf{p}$.
$\\$ 注意到$\mathbf{p}(0) = \mathbf{e}$, $\mathbf{p}(1) = \mathbf{s}$, 更一般地, 若$0 < t_1 < t_2$, 那么$\mathbf{p}(t_1)$比$\mathbf{p}(t_2)$更接近观察点$\mathbf{e}$. 同样地, 若$t < 0$, 那么$\mathbf{p}(t)$在观察点$\mathbf{e}$后. 当我们寻找光线击中的离观察点$\mathbf{e}$最近且不在$\mathbf{e}$后面的物体时, 这些性质将十分有用.
$\\$ 接下来, 我们需要确定图像在像平面上的位置(即确定像平面上的点$\mathbf{s}$). 设像平面上的一点为$O$, 以点$O$为起点的两条相互垂直的射线为$$\mathbb{r}_1(t) = O + t \mathbf{u}, \\ \mathbb{r}_2(t) = O + t \mathbf{v},$$其中, $\mathbf{u}$, $\mathbf{v}$分别为两条射线$\mathbb{r}_1(t)$, $\mathbb{r}_2(t)$对应的方向向量. 图像左, 右边缘所在的直线与射线$\mathbb{r}_1(\mathbf{s})$所在的直线的交点分别为$O + L \mathbf{u}$, $O $$ + R \mathbf{u}$; 图像上, 下边缘所在的直线与射线$\mathbb{r}_2(t)$所在的直线的交点分别为$O + $$ T \mathbf{v}$, $O + B \mathbf{v}$. 一般来说, $L < $$ 0 < R$, $B < 0 < T$.
$\\$ 为了将含有$n_x \times n_y$个像素的图像放入大小为$(R − L) \times $$ (T − B)$的矩形中, 像素间的水平间隔应为$(R − L) / n_x$, 垂直间隔应为$(T − B $$ ) / n_y$. 这样一来, 我们也将矩形划分为$n_x \times n_y$个格子. 此外, 在图像边缘处还需留出半个像素大小的空间, 使得每一个像素均在所处的矩形格子内居中, 即光栅化图像中坐标为$(i, $$ j)$的像素的位置为$$u = L + (R − L)(i + 0.5) / n_x, \\ v = B + (T − B)(j + 0.5) / n_y,$$其中, $(u, v)$为像素在像平面上的位置坐标.
$\\$
$\\$ 2. 光线与物体的相交计算
2.1 光线与球的相交计算
给定一条光线$\mathbf{p}(t) = \mathbf{e} + t\mathbf{d}$与一个隐式曲面$f(\mathbf{p}) = 0$, 其交点需要同时在光线与隐式曲面上, 故待求的$t$满足下述方程$$f(\mathbf{p}(t)) = 0, f(\mathbf{e} + t\mathbf{d}) = 0.$$一个球心为$\mathbf{c} = (x_\mathbf{c}, y_\mathbf{c}, z_\mathbf{c})^T$, 半径为$R$的球可以使用下述隐式方程表示:$$(x – x_\mathbf{c})^2 + (y – y_\mathbf{c})^2 + (z – z_\mathbf{c})^2 – R^2 = 0.$$我们可以把上述方程写为向量形式:$$(\mathbf{p} – \mathbf{c}) \cdot (\mathbf{p} – \mathbf{c}) – R^2 = 0.$$球面上的任意点$\mathbf{p}$均满足上述方程. 若我们把光线$\mathbf{p}(t) = \mathbf{e} + t\mathbf{d}$上的点代入上述方程, 我们可以得到一个关于$t$的方程:$$(\mathbf{e} + t\mathbf{d} – \mathbf{c}) \cdot (\mathbf{e} + t\mathbf{d} – \mathbf{c}) – R^2 = 0.$$合并同类项可得$$(\mathbf{d} \cdot \mathbf{d})t^2 + 2\mathbf{d} \cdot (\mathbf{e} – \mathbf{c})t + (\mathbf{e} – \mathbf{c}) \cdot (\mathbf{e} – \mathbf{c}) – R^2 = 0.$$解之,$$t = \frac{-\mathbf{d} \cdot (\mathbf{e} – \mathbf{c}) \pm \sqrt{(\mathbf{d} \cdot (\mathbf{e} – \mathbf{c}))^2 – (\mathbf{d} \cdot \mathbf{d})((\mathbf{e} – \mathbf{c}) \cdot (\mathbf{e} – \mathbf{c}) – R^2)}}{(\mathbf{d} \cdot \mathbf{d})}.$$实际计算中, 在计算其它项之前, 应该首先检查判别式的值. 若球体仅被用作更复杂的对象的Bounding Sphere, 那么我们仅需要确定是否命中它(检查判别式) 就足够了. 此外, 点$\mathbf{p}$处的单位法向量为$(\mathbf{p} − $$ \mathbf{c}) / R$.
2.2 光线与三角形的相交计算
为了求得光线$\mathbf{e} + t\mathbf{d}$与参数曲面$F(u, v)$的交点, 我们可以建立一个基于笛卡尔坐标系的方程组:$$\left.\begin{matrix}
x_\mathbf{e} + tx_\mathbf{d} = f(u, v) \\
y_\mathbf{e} + ty_\mathbf{d} = g(u, v) \\
z_\mathbf{e} + tz_\mathbf{d} = h(u, v)
\end{matrix}\right\} \ or, \ \mathbf{e} + t\mathbf{d} = F(u, v).$$这样一来, 我们得到了3个方程与3个未知数($t$, $u$与$v$), 当使用解析的方法无法得到解或者得到解的代价较高时, 我们亦可以使用数值方法进行求解.
$\\$ 若三角形的三个顶点分别为$\mathbf{a}$, $\mathbf{b}$与$\mathbf{c}$, 则其交点满足下述方程:$$\mathbf{e} + t\mathbf{d} = \mathbf{a} + \beta(\mathbf{b} – \mathbf{a}) + \gamma(\mathbf{c} – \mathbf{a}).$$易知, 交点在三角形内当且仅当$\beta > 0$, $\gamma > 0$, 且$\beta + \gamma < 1$. 否则, 交点将在三角形外或三角形边界上. 若上述方程无解, 要么三角形是退化的, 要么光线平行于三角形所在的平面.
$\\$ 为了求得$t$, $\beta$与$\gamma$, 我们将上述方程从向量形式展开为3个方程:$$x_\mathbf{e} + tx_\mathbf{d} = x_\mathbf{a} + \beta(x_\mathbf{b} - x_\mathbf{a}) + \gamma(x_\mathbf{c} - x_\mathbf{a}), \\ y_\mathbf{e} + ty_\mathbf{d} = y_\mathbf{a} + \beta(y_\mathbf{b} - y_\mathbf{a}) + \gamma(y_\mathbf{c} - y_\mathbf{a}), \\ z_\mathbf{e} + tz_\mathbf{d} = z_\mathbf{a} + \beta(z_\mathbf{b} - z_\mathbf{a}) + \gamma(z_\mathbf{c} - z_\mathbf{a}).$$上述方程组可以标准线性系统的形式写为:$$\begin{bmatrix}
x_\mathbf{a} - x_\mathbf{b} & x_\mathbf{a} - x_\mathbf{c} & x_\mathbf{d} \\
y_\mathbf{a} - y_\mathbf{b} & y_\mathbf{a} - y_\mathbf{c} & y_\mathbf{d} \\
z_\mathbf{a} - z_\mathbf{b} & z_\mathbf{a} - z_\mathbf{c} & z_\mathbf{d}
\end{bmatrix} \begin{bmatrix}
\beta \\
\gamma \\
t
\end{bmatrix} = \begin{bmatrix}
x_\mathbf{a} - x_\mathbf{e} \\
y_\mathbf{a} - y_\mathbf{e} \\
z_\mathbf{a} - z_\mathbf{e}
\end{bmatrix}.$$求解这个$3 \times 3$的线性方程组最快的经典方法是克莱默法则, 由此可得$$\beta = \frac{\begin{vmatrix}
x_\mathbf{a} - x_\mathbf{e} & x_\mathbf{a} - x_\mathbf{c} & x_\mathbf{d} \\
y_\mathbf{a} - y_\mathbf{e} & y_\mathbf{a} - y_\mathbf{c} & y_\mathbf{d} \\
z_\mathbf{a} - z_\mathbf{e} & z_\mathbf{a} - z_\mathbf{c} & z_\mathbf{d}
\end{vmatrix}}{|A|}, \\ \gamma= \frac{\begin{vmatrix}
x_\mathbf{a} - x_\mathbf{b} & x_\mathbf{a} - x_\mathbf{e} & x_\mathbf{d} \\
y_\mathbf{a} - y_\mathbf{b} & y_\mathbf{a} - y_\mathbf{e} & y_\mathbf{d} \\
z_\mathbf{a} - z_\mathbf{b} & z_\mathbf{a} - z_\mathbf{e} & z_\mathbf{d}
\end{vmatrix}}{|A|}, \\ t= \frac{\begin{vmatrix}
x_\mathbf{a} - x_\mathbf{b} & x_\mathbf{a} - x_\mathbf{c} & x_\mathbf{a} - x_\mathbf{e} \\
y_\mathbf{a} - y_\mathbf{b} & y_\mathbf{a} - y_\mathbf{c} & y_\mathbf{a} - y_\mathbf{e} \\
z_\mathbf{a} - z_\mathbf{b} & z_\mathbf{a} - z_\mathbf{c} & z_\mathbf{a} - z_\mathbf{e}
\end{vmatrix}}{|A|},$$其中, 矩阵$A$为$$A = \begin{bmatrix}
x_\mathbf{a} - x_\mathbf{b} & x_\mathbf{a} - x_\mathbf{c} & x_\mathbf{d} \\
y_\mathbf{a} - y_\mathbf{b} & y_\mathbf{a} - y_\mathbf{c} & y_\mathbf{d} \\
z_\mathbf{a} - z_\mathbf{b} & z_\mathbf{a} - z_\mathbf{c} & z_\mathbf{d}
\end{bmatrix},$$$|A|$表示矩阵$A$的行列式. 我们可以将上述线性系统简记为$$\begin{bmatrix}
a & d & g \\
b & e & h \\
c & f & i
\end{bmatrix} \begin{bmatrix}
\beta \\
\gamma \\
t
\end{bmatrix} = \begin{bmatrix}
j \\
k \\
l
\end{bmatrix},$$由克拉默法则可得$$\beta = \frac{j(ei - hf) + k(gf - di) + l(dh - eg)}{M}, \\ \gamma = \frac{i(ak - jb) + h(jc - al) + g(bl - kc)}{M}, \\ t = \frac{f(ak - jb) + e(jc - al) + d(bl - kc)}{M},$$其中,$$M = a(ei - hf) + b(gf - di) + c(dh - eg).$$我们可以通过缓存重复计算的式子来减少运算量, 如$ei - hf$.
$\\$
$\\$ 2.3 光线与多边形的相交计算
给定一个平面多边形, 有$m$个顶点$\mathbf{p}_1$到$\mathbf{p}_m$, 其面法线为$\mathbf{n}$, 我们利用隐式方程计算射线$\mathbf{e} + t\mathbf{d}$与该多边形所在的平面的交点:$$(\mathbf{p} – \mathbf{p}_1) \cdot \mathbf{n} = 0.$$设$\mathbf{p} = \mathbf{e} + t\mathbf{d}$, 求解$t$得$$t = \frac{(\mathbf{p}_1 – \mathbf{e}) \cdot \mathbf{n}}{\mathbf{d} \cdot \mathbf{n}}.$$从而我们可得$\mathbf{p}$. 若$\mathbf{p}$在多边形内, 则说明光线命中该多边形.
$\\$ 我们可以通过将点与多边形顶点均投影到$XOY$平面上来判断点$\mathbf{p}$是否在多边形内. 最简单的方法是从点$\mathbf{p}$发射任意2D射线, 并计算该射线与多边形边界之间的交点数. 若交点数为奇数, 则该点在多边形内; 否则, 该点在多边形外. 直观上理解, 若射线是从多边形外发射, 则必产生一对交点, 从而其交点数必为偶数. 为了简化计算, 我们通常直接选择沿$x$轴方向发射的2D射线:$$\begin{bmatrix}
x \\
y
\end{bmatrix} = \begin{bmatrix}
x_\mathbf{p} \\
y_\mathbf{p}
\end{bmatrix} + s\begin{bmatrix}
1 \\
0
\end{bmatrix},$$其中, $s \in (0, +\infty)$. 显然, 计算该射线与多边形边界的交点是比较简单的.
3. 着色模型
3.1 Lambertian着色模型
最简单的光照模型是基于Lambertian在18世纪所做的观察: 来自光源的能量落在物体表面上的面积取决于物体表面与光线的角度. 一个垂直于光线的物体表面接收最大强度的光照; 与光线方向相切(或背向光源) 的物体表面无法接收光照; 除上述两种情况以外, 物体表面接收的光照强度与表面法线和光线之间的夹角的余弦值成正比. 这也就引出了Lambertian着色模型:$$L = k_d I max(0, \mathbf{n} \cdot \mathbf{l}),$$其中, $L$为像素颜色; $k_d$为扩散系数; $I$为光源强度. 因为法向量$\mathbf{n}$与光线的方向向量$\mathbf{l}$均为单位向量, 故$\mathbf{n} \cdot \mathbf{l}$即为$cos \theta$($\theta$为法向量$\mathbf{n}$与光线的方向向量$\mathbf{l}$之间的夹角). 上述模型分别适用于3个颜色通道, 故像素值的红色分量为扩散系数, 光源强度的红色通道值, 与法向量与光线的方向向量的内积的乘积; 对于绿色通道与蓝色通道亦是如此.
3.2 Blinn-Phong着色模型
Phong光照不仅对真实光照有很好的近似, 而且性能也很高. 但是它的镜面反射会在一些情况下出现问题, 特别是物体反光度很低时, 会导致大片(粗糙的) 高光区域. 下面这张图展示了当反光度为1.0时地板会出现的效果:

可以看到, 在镜面高光区域的边缘出现了一道很明显的断层. 出现这个问题的原因是观察向量和反射向量间的夹角不能大于90度. 如果点积的结果为负数, 镜面光分量会变为0.0. 你可能会觉得, 当光线与视线夹角大于90度时你应该不会接收到任何光才对, 所以这不是什么问题.
$\\$ 然而, 这种想法仅仅只适用于漫反射分量. 当考虑漫反射光的时候, 如果法线和光源夹角大于90度, 光源会处于被照表面的下方, 这个时候光照的漫反射分量的确是为0.0. 但是, 在考虑镜面高光时, 我们测量的角度并不是光源与法线的夹角, 而是视线与反射光线向量的夹角. 看一下下面这两张图:

现在问题就应该很明显了. 左图中是我们熟悉的Phong光照中的反射向量, 其中$\theta$角小于90度. 而右图中, 视线与反射方向之间的夹角明显大于90度, 这种情况下镜面光分量会变为0.0. 这在大多数情况下都不是什么问题, 因为观察方向离反射方向都非常远. 然而, 当物体的反光度非常小时, 它产生的镜面高光半径足以让这些相反方向的光线对亮度产生足够大的影响. 在这种情况下就不能忽略它们对镜面光分量的贡献了.
$\\$ 1977年, James F. Blinn在Phong着色模型上加以拓展, 引入了Blinn-Phong着色模型. Blinn-Phong模型与Phong模型非常相似, 但是它对镜面光模型的处理上有一些不同, 让我们能够解决之前提到的问题. Blinn-Phong模型不再依赖于反射向量, 而是采用了所谓的半程向量(Halfway Vector), 即光线与视线夹角一半方向上的一个单位向量. 当半程向量与法线向量越接近时, 镜面光分量就越大.
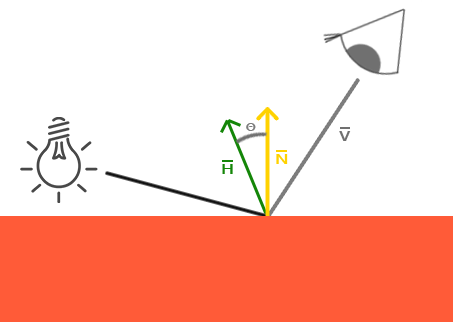
当视线正好与(现在不需要的) 反射向量对齐时, 半程向量就会与法线完美契合. 所以当观察者视线越接近于原本反射光线的方向时, 镜面高光就会越强.
$\\$ 现在, 不论观察者向哪个方向看, 半程向量与表面法线之间的夹角都不会超过90度(除非光源在表面以下). 它产生的效果会与冯氏光照有些许不同, 但是大部分情况下看起来会更自然一点, 特别是低高光的区域. Blinn-Phong着色模型正是早期固定渲染管线时代时OpenGL所采用的光照模型.
$\\$ 获取半程向量的方法很简单, 只需要将光线的方向向量和观察向量加到一起, 并将结果正规化(Normalize) 就可以了:$$\mathbf{h} = \frac{\mathbf{v} + \mathbf{l}}{\left \| \mathbf{v} + \mathbf{l} \right \|}.$$接下来, 镜面光分量的实际计算只不过是对表面法线和半程向量进行一次约束点乘(Clamped Dot Product), 让点乘结果不为负, 从而获取它们之间夹角的余弦值, 之后我们对这个值取反光度次方, 故Blinn-Phong着色模型如下所示:$$L = k_d I max(0, \mathbf{n} \cdot \mathbf{l}) + k_s I max(0, \mathbf{n} \cdot \mathbf{h})^p,$$其中, $k_s$为镜面高光系数. 除此之外Blinn-Phong模型就没什么好说的了, Blinn-Phong与Phong模型唯一的区别就是, Blinn-Phong测量的是法线与半程向量之间的夹角, 而Phong模型测量的是观察方向与反射向量间的夹角.
$\\$ 在引入半程向量之后, 我们现在应该就不会再看到Phong光照中高光断层的情况了. 下面两个图片展示的是两种方法在镜面光分量为0.5时的对比:
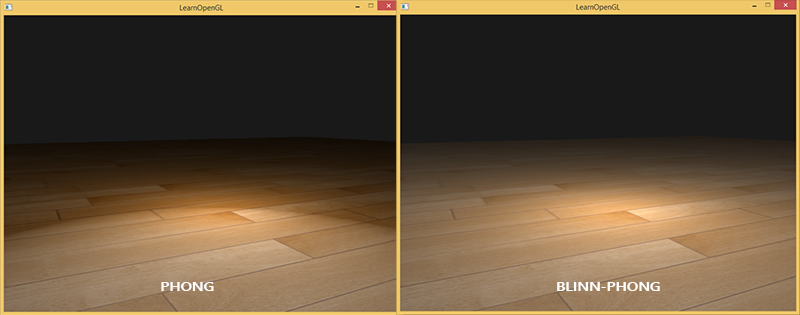
除此之外, Phong模型与Blinn-Phong模型也有一些细微的差别: 半程向量与表面法线的夹角通常会小于观察与反射向量的夹角. 所以, 如果你想获得和冯氏着色类似的效果, 就必须在使用Blinn-Phong模型时将镜面反光度设置更高一点. 通常我们会选择Phong着色模型时反光度分量的2到4倍.
$\\$ 下面是Phong着色反光度为8.0, Blinn-Phong着色反光度为32.0时的一个对比:

你可以看到, Blinn-Phong的镜面光分量会比Phong模型更锐利一些. 为了得到与冯氏模型类似的结果, 你可能会需要不断进行一些微调, 但Blinn-Phong模型通常会产出更真实的结果.
3.3 环境光着色模型
没有接收到直接光照的物体表面将直接被渲染为黑色, 这通常是不可取的. 在实际应用中, 为了避免渲染纯黑的物体表面, 通常是向着色模型中添加一个常量项, 该项完全不依赖于物体表面的几何信息. 这就是所谓的环境光着色——就好像物体表面被来自各个地方的”环境”光照亮. 为了方便调整参数, 环境光着色模型通常表示为物体表面的环境光系数与环境光强度的乘积的形式, 因此环境光着色模型可以为单个物体表面进行调整, 亦可以为所有的物体表面一并调整. 与Blinn-Phong着色模型进行组合, 便得到了一个简单且有用的着色模型的完整版本:$$L = k_a I_a + k_d I max(0, \mathbf{n} \cdot \mathbf{l}) + k_s I max(0, \mathbf{n} \cdot \mathbf{h})^n,$$其中, $k_a$为环境光系数, $I_a$为环境光强度.
3.4 多个点光源
光具有波和粒子的特性. 当两束光在空间中相遇, 光的叠加不是强度的叠加. 然而在实际应用中, 我们会将着色模型简单地扩展到$N$个光源的情形:$$L = k_a I_a + \sum_{i = 1}^{N}[k_d I_i max(0, \mathbf{n} \cdot \mathbf{l_i}) + k_s I_i max(0, \mathbf{n} \cdot \mathbf{h_i})^p],$$其中, $I_i$, $\mathbf{l_i}$与$\mathbf{h_i}$分别为第$i$个光源的强度, 对应的光线的方向向量与对应的半程向量.
4. 理想的镜面反射
在光线追踪的代码中加入理想的镜面反射是比较简单的. 易知, 当观察者从方向$\mathbf{e}$看向一个物体时, 其理想的镜面反射向量$\mathbf{r}$为:$$\mathbf{r} = \mathbf{d} – 2(\mathbf{d} \cdot \mathbf{n})\mathbf{n},$$其中, $\mathbf{d} = -\mathbf{e}$为指向物体表面的向量.
$\\$ 在现实世界中, 当光线经物体表面反射后, 会损失一些能量. 这种损失对于不同颜色的物体表面可能是不同的. 例如, 金色物体比蓝色物体能够更有效地反射黄色光线. 这可以通过在光线追踪的代码中添加一个递归调用来实现:
color c = c + k_m * raycolor(p + s * r, varepsilon, infty)
其中, $k_m$为镜面反射系数. 为了避免我们反射光线击中产生它的物体, 我们需要确保$s \in [\varepsilon, +\infty]$.
$\\$ 上面的递归调用的问题是它可能永远不会终止. 例如, 如果一束光线从房间内某处开始, 它将永远反弹下去. 因此, 在实际应用中, 我们需要通过限制最大的递归深度来解决这个问题. 此外, 若$k_m = 0$, 则不应该生成反射光线.
5. 常见问题
问1: 为什么在光线追踪中没有透视矩阵?
$\\$ 答1: 通过从观察点向外发射光线本身就是一个模拟透视投影的过程.
问2: 光线追踪可以应用在游戏中吗?
$\\$ 答2: 随着计算机算力越来越强, 对于场景较简单的游戏, 已经可以实现光线追踪了. 实际上, 计算机性能的增长速度远远快于屏幕分辨率的增长速度, 传统PC实现复杂场景的光线追踪只是时间问题.
问3: 光线追踪目前有什么成熟的应用场景吗?
$\\$ 答3: 光线追踪经常用于拾取对象的获取. 当用户在3D图形程序的界面上点击鼠标时, 程序需要确定在该像素内哪个对象是可见的, 而光线追踪是确定这一点的理想方法.
6. 相关习题
6.1 求使得射线$(1, 1, 1)^T + t(-1, -1, -1)^T$与球心为原点的单位球相交的$t$的值.
$\\$ 解: 先计算相交的判别式, 由2.1小节的计算公式可得$\triangle = 3 > 0$, 故该射线与单位球之间存在两个交点对应的$t$的值: $t = \frac{3 \pm \sqrt{3}}{3}$.
6.2 求使得射线$(1, 1, 1)^T + t(-1, -1, -1)^T$与三个顶点分别为$(1, 0, 0)^T$, $(0, 1, 0)^T$与$(0, 0, 1)^T$的三角形相交的$t$的值, 并求出交点关于该三角形的重心坐标.
$\\$ 解: 先计算对应的线性系统的系数矩阵的行列式, 由2.2小节的计算公式可得$|A| = -2 \ne 0$, 故该射线与该三角形所在的平面存在唯一交点. 接下来计算该交点是否在三角形内.
$\\$ 易知, $\beta = 0.5$, $\gamma = 0.5$, $t = 0.5$, 从而交点关于该三角形的重心坐标为$(0, 0.5 $$ , 0.5)^T$, 即该交点位于三角形的边界上.