目前已经在新公司工作了一周多了, 前面两天确实有点吃不消(包括通勤时间与工作时间等因素), 但现在也逐渐适应了目前的工作节奏. 虽然干的活基本还是脏活, 但对未来总归还是有盼头, 希望未来还是能接几何形状分析相关的工作内容叭(例如PCG与PVS)~ 这周的博客进度有点慢, 本来以为能快速解决掉线性代数相关的内容, 结果……囧( ╯□╰ ) 变换矩阵虽然用得比较多了, 但读完Shirley P, Ashikhmin M, Marschner S. Fundamentals of computer graphics[M]. AK Peters/CRC Press, 2009.的第6章, 犹如醍醐灌顶, 仿佛发现了一个新世界~ 因此, 本文是不得不将这些闪光点记录下来滴!
参考材料
1. How can you show that the inverse of the matrix for an affine transformation (one that has all zeros in the bottom row except for a one in the lower right entry) also has the same form?
2. Affine transformation
1. 2维线性变换
我们可以使用一个$2 \times 2$的矩阵来变换一个2维向量:$$\begin{bmatrix}
a_{11} & a_{12}\\
a_{21} & a_{22}
\end{bmatrix}\begin{bmatrix}
x \\
y
\end{bmatrix} = \begin{bmatrix}
a_{11}x + a_{12}y \\
a_{21}x + a_{22}y
\end{bmatrix}.$$这种将一个2维向量通过简单的矩阵乘法得到另外一个2维向量的变换为一个线性变换.
1.1 缩放
最基本的变换为沿着坐标轴的缩放, 这个变换可以改变向量的长度与方向:$$scale(s_x, s_y) = \begin{bmatrix}
s_x & 0\\
0 & s_y
\end{bmatrix}.$$当上述矩阵作用在笛卡尔坐标$(x, y)$后可得:$$\begin{bmatrix}
s_x & 0\\
0 & s_y
\end{bmatrix} \begin{bmatrix}
x \\
y
\end{bmatrix} = \begin{bmatrix}
s_x x \\
s_y y
\end{bmatrix}.$$因此, 我们可以从一个轴对齐的缩放矩阵中直接得到2个缩放的比例因子.
1.2 剪切
从直观上来理解, 剪切变换是一种把作用对象推往一边的变换. 水平方向与竖直方向上的剪切矩阵分别为$$shear-x(s) = \begin{bmatrix}
1 & s\\
0 & 1
\end{bmatrix}, shear-y(s) = \begin{bmatrix}
1 & 0\\
s & 1
\end{bmatrix}.$$另一种理解剪切的角度是只考虑竖直轴(或水平轴) 的旋转. 水平方向上的剪切变换为取竖直轴并顺时针倾斜角度$\phi$:$$\begin{bmatrix}
1 & tan \phi\\
0 & 1
\end{bmatrix}.$$同理, 竖直方向上的剪切变换为取水平轴并逆时针倾斜角度$\phi$:$$\begin{bmatrix}
1 & 0\\
tan \phi & 1
\end{bmatrix}.$$
1.3 旋转
设向量$\mathbf{a}$与$x$轴的夹角为$\alpha$, 其长度为$r = x_\mathbf{a}^2 + y_\mathbf{a}^2$, $\mathbf{b}$为向量$\mathbf{a}$逆时针旋转角度$\phi$得到的向量, 则$$x_\mathbf{a} = rcos\alpha, \\ y_\mathbf{a} = rsin\alpha.$$由于向量$\mathbf{b}$是通过将向量$\mathbf{a}$逆时针旋转角度$\phi$得到的, 故其长度也为$r$, 与$x$轴的夹角为$(\alpha + \phi)$. 由三角函数的积化和差公式可得:$$x_\mathbf{b} = rcos(\alpha + \phi) = r cos\alpha cos\phi – r sin\alpha sin\phi, \\ y_\mathbf{b} = rsin(\alpha + \phi) = r sin\alpha cos\phi + r cos\alpha sin\phi.$$代入$x_\mathbf{a} = rcos\alpha$与$y_\mathbf{a} = rsin\alpha$可得$$x_\mathbf{b} = x_\mathbf{a} cos\phi – y_\mathbf{a} sin\phi, \\ y_\mathbf{b} = y_\mathbf{a} cos\phi + x_\mathbf{a} sin\phi.$$采用矩阵的语言描述上述变换,$$rotate(\phi) = \begin{bmatrix}
cos\phi & -sin\phi\\
sin\phi & cos\phi
\end{bmatrix}.$$
1.4 反射
我们可以通过使用带有一个负比例因子的矩阵, 来得到关于特定坐标轴的反射向量:$$reflect-y = \begin{bmatrix}
-1 & 0\\
0 & 1
\end{bmatrix}, relfect-x = \begin{bmatrix}
1 & 0\\
0 & -1
\end{bmatrix}.$$
1.5 变换的组合
在图形程序中, 对一个对象应用多个变换是十分常见的. 例如, 我们可能想对一个2维向量$\mathbf{v}_1$先应用缩放矩阵$\mathbf{S}$, 再应用旋转矩阵$\mathbf{R}$, 这可以分两步完成:$$\mathbf{v}_2 = \mathbf{S} \mathbf{v}_1, \mathbf{v}_3 = \mathbf{R} \mathbf{v}_2.$$另一种写法是$$\mathbf{v}_3 = \mathbf{R} (\mathbf{S} \mathbf{v}_1).$$由于矩阵乘法是满足结合律的, 故我们也可以写成$$\mathbf{v}_3 = (\mathbf{R} \mathbf{S})\mathbf{v}_1.$$换句话说, 我们可以用一个相同大小的矩阵来表示用两个矩阵依次变换一个向量的效果, 即可以通过将两个矩阵相乘来计算:$$\mathbf{M} = \mathbf{R} \mathbf{S}.$$需要注意的是, 这些变换是从右边开始应用的. 对于矩阵$\mathbf{M} = \mathbf{R} \mathbf{S}$而言, 我们首先应用缩放变换$\mathbf{S}$, 然后应用旋转变换$\mathbf{R}$.
1.6 变换的分解
$\cdot$ 实对称矩阵的特征值分解
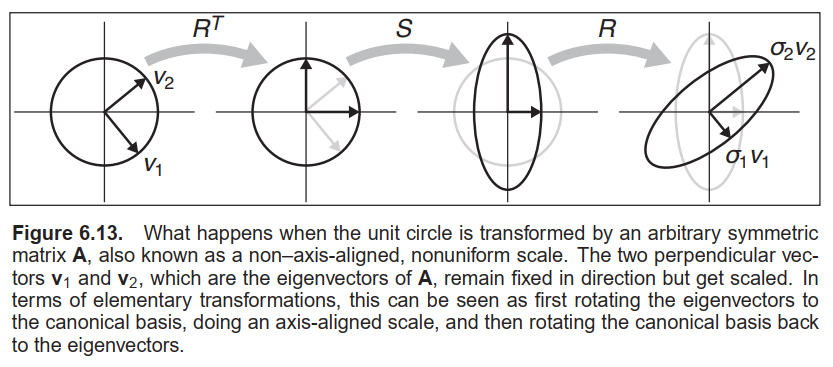
我们从实对称矩阵开始. 一个实对称矩阵总可以进行特征值分解$$\mathbf{A} = \mathbf{R} \mathbf{S} \mathbf{R}^T,$$其中, $\mathbf{R}$为正交矩阵, $\mathbf{S}$为对角矩阵; 我们称正交矩阵$\mathbf{R}$的列向量(特征向量) 为$\mathbf{v}_1$与$\mathbf{v}_2$, 称对角矩阵$\mathbf{S}$的对角线元素(特征值) 为$\lambda_1$与$\lambda_2$.
$\\$从几何上来看, 我们可以将正交矩阵$\mathbf{R}$视为旋转变换, 将对角矩阵$\mathbf{S}$视为缩放变换, 因此这是一个多步的几何变换:
$\\$ (1) 将与特征向量$\mathbf{v}_1$共线的向量和与特征向量$\mathbf{v}_2$共线的向量分别旋转到$x$轴上与$y$轴上(通过正交矩阵$\mathbf{R}^T$进行变换).
$\\$ (2) 分别沿$x$轴与$y$轴以缩放因子$\lambda_1$与$\lambda_2$进行缩放(通过对角矩阵$\mathbf{S}$进行变换).
$\\$ (3) 将与$x$轴共线的向量和与$y$轴共线的向量分别旋转至与特征向量$\mathbf{v}_1$共线和与特征向量$\mathbf{v}_2$共线(通过正交矩阵$\mathbf{R}$进行变换).
$\\$ 把上述3个变换放在一起看, 我们可以看到它们在实对称矩阵$\mathbf{A}$的特征向量对应的一对坐标轴上(亦是相互垂直的) 具有不均匀尺度的效果. 这告诉了我们什么是实对称矩阵: 实对称矩阵只是对应一个缩放变换——尽管可能是非均匀的与非轴对齐的.
我们也可以反转上述的对角化过程; 以$(\lambda_1, \lambda_2)$为缩放因子, 从$x$轴顺时针方向旋转角度$\phi$, 则我们有$$\begin{bmatrix}
cos\phi & sin\phi\\
-sin\phi & cos\phi
\end{bmatrix} \begin{bmatrix}
\lambda_1 & 0\\
0 & \lambda_2
\end{bmatrix} \begin{bmatrix}
cos\phi & -sin\phi\\
sin\phi & cos\phi
\end{bmatrix} = \\
\begin{bmatrix}
\lambda_1 cos^2\phi + \lambda_2 sin^2\phi & (\lambda_2 – \lambda_1) cos\phi sin\phi\\
(\lambda_2 – \lambda_1) cos\phi sin\phi & \lambda_2 cos^2\phi + \lambda_1 sin^2\phi
\end{bmatrix}.$$值得注意的是, 这是一个对称矩阵, 因为其是以实对称矩阵的特征值分解的形式构造的.
$\cdot$ 奇异值分解
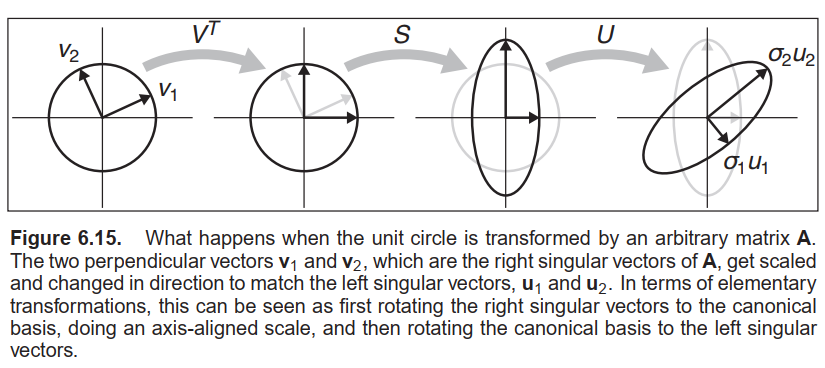
一种非常类似的分解也可以用于非对称矩阵: 它便是奇异值分解(SVD). 它与实对称矩阵的特征值分解的不同之处在于对角矩阵两侧的矩阵不再要求相同:$$\mathbf{A} = \mathbf{U} \mathbf{S} \mathbf{V}^T.$$代替单次旋转矩阵$\mathbf{R}$的两个正交矩阵分别为$\mathbf{U}$与$\mathbf{V}$, 它们的列向量分别记为$\mathbf{u}_i$(左奇异向量) 与$\mathbf{v}_i$(右奇异向量). 在这种情况下, 对角矩阵$\mathbf{S}$的对角线元素被称为奇异值而非特征值. 其几何解释与实对称矩阵的特征值分解非常相似:
$\\$ (1) 将与奇异向量$\mathbf{v}_1$共线的向量和与奇异向量$\mathbf{v}_2$共线的向量分别旋转到$x$轴上与$y$轴上(通过正交矩阵$\mathbf{V}^T$进行变换).
$\\$ (2) 分别沿$x$轴与$y$轴以缩放因子$\sigma_1$与$\sigma_2$进行缩放变换(通过对角矩阵$\mathbf{S}$进行变换).
$\\$ (3) 将与$x$轴共线的向量和与$y$轴共线的向量分别旋转至与奇异向量$\mathbf{u}_1$共线和与奇异向量$\mathbf{u}_2$共线(通过正交矩阵$\mathbf{U}$进行变换).
$\\$ 主要的区别为一个旋转矩阵与两个不同的正交矩阵之间的区别, 这种差异诱导了SVD的一个可能不起眼的特征. 由于SVD的两边的奇异向量可能不同, 所以不需要负奇异值: 我们总是可以反转一个奇异值的符号, 再反转其中一个对应的奇异向量的方向, 从而再次得到相同的变换. 由于这个原因, SVD得到的对角矩阵的对角线元素总为正数, 但正交矩阵$\mathbf{U}$与正交矩阵$\mathbf{V}$无法保证是旋转矩阵——它们亦可能为反射矩阵. 在图形程序中, 这很不方便, 但我们可以通过一个小技巧来规避这个问题: 通过检查行列式, 我们可以很容易地区分旋转矩阵与反射矩阵, 因为旋转矩阵的行列式为+1, 而反射矩阵的行列式为−1. 如此一来, 若通过SVD得到的某个正交矩阵(如正交矩阵$\mathbf{U}$) 为反射矩阵, 而我们希望对角矩阵$\mathbf{S}$两侧的正交矩阵均为旋转矩阵, 则我们可以将其中一个奇异值的符号进行反转得到新的对角矩阵$\mathbf{S}’$, 同时将正交矩阵$\mathbf{U}$中对应的奇异向量的方向一并进行反转得到新的正交矩阵$\mathbf{U}’$, 则此时$\mathbf{A} = \mathbf{U}’ \mathbf{S}’ \mathbf{V}^T$, 对角矩阵$\mathbf{S}’$两侧的正交矩阵均为旋转矩阵.
$\cdot$ 旋转矩阵的Paeth分解
非零的旋转矩阵可以利用剪切变换进行分解(Paeth, 1990), 即$$\begin{bmatrix}
cos\phi & sin\phi\\
-sin\phi & cos\phi
\end{bmatrix} = \begin{bmatrix}
1 & \frac{cos\phi – 1}{sin\phi}\\
0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0\\
sin\phi & 1
\end{bmatrix} \begin{bmatrix}
1 & \frac{cos\phi – 1}{sin\phi}\\
0 & 1
\end{bmatrix}.$$这种特殊的变换对光栅化图像上的旋转变换很有用, 因为剪切变换是一种非常有效的图像光栅操作; 它会产生一些锯齿, 但不会留下洞. 值得注意的是, 若我们取光栅化图像上的一个像素(其坐标为$(i, j)$), 并对其应用水平方向上的剪切变换, 可得$$\begin{bmatrix}
1 & s\\
0 & 1
\end{bmatrix} \begin{bmatrix}
i \\
j
\end{bmatrix} = \begin{bmatrix}
i + sj \\
j
\end{bmatrix}.$$若我们将$sj$四舍五入到最接近的整数, 这相当于取图像中的每一行并将其向一侧移动一定的量——每行移动的量均不同. 对于图像中同一行内的每个像素, 其位移量均相同, 这允许我们在结果图像中不能出现洞的前提下进行旋转变换. 竖直方向上的剪切变换也起到类似的作用. 如此一来, 我们便可以很容易地实现光栅化图像上的旋转变换.
2. 3维线性变换
3维线性变换为2维线性变换的扩展. 例如, 沿着笛卡尔坐标轴的缩放矩阵为$$scale(s_x, s_y, s_z) = \begin{bmatrix}
s_x & 0 & 0\\
0 & s_y & 0\\
0 & 0 & s_z
\end{bmatrix}.$$在3维空间中进行旋转变换要比在2维空间中复杂得多, 因为有更多可能的旋转轴. 然而, 若我们只是想绕$z$轴旋转, 则仅会改变其笛卡尔坐标的$x$分量与$y$分量, 我们可以使用不对笛卡尔坐标的$z$分量进行操作的2维旋转矩阵:$$rotate-z(\phi) = \begin{bmatrix}
cos\phi & -sin\phi & 0\\
sin\phi & cos\phi & 0\\
0 & 0 & 1
\end{bmatrix}.$$类似地, 我们可以构造矩阵来围绕$x$轴与$y$轴旋转:$$rotate-x(\phi) = \begin{bmatrix}
1 & 0 & 0\\
0 & cos\phi & -sin\phi\\
1 & sin\phi & cos\phi
\end{bmatrix}, \\ rotate-y(\phi) = \begin{bmatrix}
cos\phi & 0 & sin\phi\\
0 & 1 & 0\\
-sin\phi & 0 & cos\phi
\end{bmatrix}.$$在3维空间中, 我们可以沿着特定的轴进行剪切变换, 如$$shear-x(d_y, d_z) = \begin{bmatrix}
1 & d_y & d_z\\
0 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}.$$与2维线性变换一样,
$\\$ $\cdot$ 任何3维线性变换矩阵都可以利用SVD分解为旋转矩阵, 缩放矩阵与另一个旋转矩阵的乘积;
$\\$ $\cdot$ 任何3维实对称矩阵都可以利用特征值分解为旋转矩阵, 缩放矩阵与反向旋转矩阵的乘积;
$\\$ $\cdot$ 3维旋转矩阵可以分解为3个3维剪切矩阵的乘积.
2.1 任意3维旋转
3维旋转矩阵为正交矩阵. 从几何上来看, 这意味着矩阵的3个行向量是相互正交的, 3个列向量亦是如此. 3维旋转矩阵的形式如下所示:$$\mathbf{R}_{\mathbf{u} \mathbf{v} \mathbf{w}} = \begin{bmatrix}
x_\mathbf{u} & y_\mathbf{u} & z_\mathbf{u}\\
x_\mathbf{v} & y_\mathbf{v} & z_\mathbf{v}\\
x_\mathbf{w} & y_\mathbf{w} & z_\mathbf{w}
\end{bmatrix}.$$其中, $\mathbf{u} = x_\mathbf{u} \mathbf{x} + y_\mathbf{u} \mathbf{y} + z_\mathbf{u} \mathbf{z}$, 同理可知$\mathbf{v}$与$\mathbf{w}$的定义. 由于$\mathbf{u}$, $\mathbf{v}$与$\mathbf{v}$这3个行向量是标准正交的, 故$$\mathbf{u} \cdot \mathbf{u} = \mathbf{v} \cdot \mathbf{v} = \mathbf{w} \cdot \mathbf{w} = 1, \\ \mathbf{u} \cdot \mathbf{v} = \mathbf{v} \cdot \mathbf{w} = \mathbf{w} \cdot \mathbf{u} = 0.$$上述旋转矩阵作用在3个行向量上具有特殊的性质, 如$$\mathbf{R}_{uvw} \mathbf{u} = \begin{bmatrix}
x_\mathbf{u} & y_\mathbf{u} & z_\mathbf{u} \\
x_\mathbf{v} & y_\mathbf{v} & z_\mathbf{v} \\
x_\mathbf{w} & y_\mathbf{w} & z_\mathbf{w}
\end{bmatrix} \begin{bmatrix}
x_\mathbf{u} \\
y_\mathbf{u} \\
z_\mathbf{u}
\end{bmatrix} = \begin{bmatrix}
x_\mathbf{u} x_\mathbf{u} + y_\mathbf{u} y_\mathbf{u} + z_\mathbf{u} z_\mathbf{u} \\
x_\mathbf{v} x_\mathbf{u} + y_\mathbf{v} y_\mathbf{u} + z_\mathbf{v} z_\mathbf{u} \\
x_\mathbf{w} x_\mathbf{u} + y_\mathbf{w} y_\mathbf{u} + z_\mathbf{w} z_\mathbf{u}
\end{bmatrix} \\ = \begin{bmatrix}
\mathbf{u} \cdot \mathbf{u} \\
\mathbf{v} \cdot \mathbf{u} \\
\mathbf{w} \cdot \mathbf{u}
\end{bmatrix} = \begin{bmatrix}
1 \\
0 \\
0
\end{bmatrix} = \mathbf{x}.$$同理可得, $\mathbf{R}_{uvw} \mathbf{v} = \mathbf{y}$, $\mathbf{R}_{uvw} \mathbf{w} = \mathbf{z}$. 故通过旋转矩阵$\mathbf{R}_{uvw}$可将行向量$\mathbf{u}$, $\mathbf{v}$与$\mathbf{w}$变换到相应的笛卡尔坐标系的坐标轴上.
$\\$ 易知, $\mathbf{R}_{uvw}^T$亦为一个正交矩阵, 且$\mathbf{R}_{uvw}^T = \mathbf{R}_{uvw}^{-1}$(正交矩阵的逆矩阵总为其转置矩阵). 重要的一点是, 对于旋转变换矩阵$\mathbf{R}_{uvw}$, 若$\mathbf{R}_{uvw}$将行向量$\mathbf{u}$变换到$x$轴上, 则$\mathbf{R}_{uvw}^T$将$x$轴上的向量变换为与行向量$\mathbf{u}$共线的向量, 同理可得$\mathbf{R}_{uvw}^T$分别作用于$y$轴上的向量与$z$轴上的向量的结果, 即$$\mathbf{R}_{uvw}^T \mathbf{y} = \begin{bmatrix}
x_\mathbf{u} & x_\mathbf{v} & x_\mathbf{w} \\
y_\mathbf{u} & y_\mathbf{v} & y_\mathbf{w} \\
z_\mathbf{u} & z_\mathbf{v} & z_\mathbf{w}
\end{bmatrix} \begin{bmatrix}
0 \\
1 \\
0
\end{bmatrix} = \begin{bmatrix}
x_\mathbf{v} \\
y_\mathbf{v} \\
z_\mathbf{v}
\end{bmatrix} = \mathbf{v}.$$故我们总是可以由一组标准正交基构建出一个旋转矩阵.
$\\$ 若我们想得到一个向量$\mathbf{v}$绕任意向量$\mathbf{a}$旋转角度$\phi$的结果, 我们可以令$\mathbf{w} = \mathbf{a}$, 从而得到一组标准正交基. 我们把向量$\mathbf{v}$由这组基向量$\mathbf{u}$, $\mathbf{v}$, $\mathbf{w}$对应的坐标系变换到笛卡尔坐标系下. 然后将向量$\mathbf{v}$绕$z$轴旋转得到向量$\mathbf{v}’$, 最后将$\mathbf{v}’$由笛卡尔坐标系变换回基向量$\mathbf{u}$, $\mathbf{v}$, $\mathbf{w}$对应的坐标系即可得到最终的旋转结果. 用矩阵的语言即可写为:$$\begin{bmatrix}
x_\mathbf{u} & x_\mathbf{v} & x_\mathbf{w} \\
y_\mathbf{u} & y_\mathbf{v} & y_\mathbf{w} \\
z_\mathbf{u} & z_\mathbf{v} & z_\mathbf{w}
\end{bmatrix} \begin{bmatrix}
cos \phi & -sin \phi & 0 \\
sin \phi & cos \phi & 0 \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x_\mathbf{u} & y_\mathbf{u} & z_\mathbf{u} \\
x_\mathbf{v} & y_\mathbf{v} & z_\mathbf{v} \\
x_\mathbf{w} & y_\mathbf{w} & z_\mathbf{w}
\end{bmatrix}.$$此外, 对于一个旋转矩阵, 我们可以计算实特征值$\lambda = 1$(旋转矩阵必定有此特征值) 对应的特征向量, 该向量是不受旋转影响的.
2.2 法向变换
若变换矩阵$\mathbf{M}$作用于曲面上的点$\mathbf{p}$, 那么于点$\mathbf{p}$处与曲面相切的向量$\mathbf{t}$在经过变换矩阵$\mathbf{M}$变换后依旧与经过变换矩阵$\mathbf{M}$变换后的点$\mathbf{p}$相切. 然而, 点$\mathbf{p}$处的曲面法向$\mathbf{n}$经过变换矩阵$\mathbf{M}$变换后可能不垂直于经过变换矩阵$\mathbf{M}$变换后的曲面.
$\\$ 我们可以推导出一个变换矩阵$\mathbf{N}$, s.t. 法向$\mathbf{n}$经变换矩阵$\mathbf{N}$作用后依旧垂直于曲面. 注意到, 对于曲面上的同一点, 其法向与其切向量是相互垂直的, 故它们的点积为0, 用矩阵的形式即可表示为$$\mathbf{n}^T \mathbf{t} = 0.$$不妨令$\mathbf{t}_\mathbf{M} = \mathbf{M} \mathbf{t}$, $\mathbf{n}_\mathbf{N} = \mathbf{N} \mathbf{n}$, 我们的目标为找到法向$\mathbf{n}$的变换矩阵$\mathbf{N}$, s.t. $\mathbf{n}_\mathbf{N}^T $$ \mathbf{t}_\mathbf{M} = 0$. 我们可以使用一些代数技巧求出变换矩阵$\mathbf{N}$. 将$\mathbf{M}^{−1} \mathbf{M} = \mathbf{I}$代入上式:$$\mathbf{n}^T \mathbf{t} = \mathbf{n}^T \mathbf{I} \mathbf{t} = \mathbf{n}^T \mathbf{M}^{−1} \mathbf{M} \mathbf{t} = 0.$$由矩阵乘法的结合律可得$$(\mathbf{n}^T \mathbf{M}^{−1}) (\mathbf{M} \mathbf{t}) = (\mathbf{n}^T \mathbf{M}^{−1}) \mathbf{t}_\mathbf{M} = 0.$$易知, 行向量$\mathbf{n}^T \mathbf{M}^{−1}$与切向量$\mathbf{t}_\mathbf{M}$垂直, 其中, $\mathbf{t}$为曲面上的点$\mathbf{p}$处的切平面上的任意切向量. 由于在三维空间中垂直于该切平面的所有向量均共线, 可知$\mathbf{n}^T \mathbf{M}^{−1}$或$-\mathbf{n}^T \mathbf{M}^{−1}$必为$\mathbf{n}_\mathbf{N}$的行向量表达式,即$\mathbf{n}_\mathbf{N}^T$, 故不妨令$$\mathbf{n}_\mathbf{N}^T = \mathbf{n}^T \mathbf{M}^{-1},$$对上式左右两边转置可得$$\mathbf{n}_\mathbf{N} = (\mathbf{n}^T \mathbf{M}^{-1})^T = (\mathbf{M}^{-1})^T \mathbf{n}.$$因此, 我们可以看到, 变换矩阵$\mathbf{M}$的逆矩阵的转置矩阵$(\mathbf{M}^{-1})^T$可以正确地变换法向$\mathbf{n}$, 使得经变换后的向量$\mathbf{n}’$垂直于经变换后的曲面上的点$\mathbf{p}$处的切平面. 由于该变换矩阵$\mathbf{N}$可能会改变法向$\mathbf{n}$的长度, 故我们总是需要对变换后的法向$\mathbf{n}’$作归一化处理. 换句话说, 我们并不关心变换后的法向$\mathbf{n}’$的长度, 即不需要精确地计算$\mathbf{M}^{-1}$, 只需要保证$\mathbf{M}^{-1}$的近似值与精确值之间仅相差一个非零的常数因子即可. 又矩阵的逆矩阵可由其伴随矩阵除以其行列式得到, 故我们可以跳过除法运算, 对于一个$3 \times 3$的变换矩阵$\mathbf{M}$,$$\mathbf{N} = \begin{bmatrix}
m_{11}^c & m_{12}^c & m_{13}^c \\
m_{21}^c & m_{22}^c & m_{23}^c \\
m_{31}^c & m_{32}^c & m_{33}^c
\end{bmatrix},$$其中, $m_{ij}$为变换矩阵$\mathbf{M}$第$i$行第$j$列的元素. 上式展开即得$$\mathbf{N} = \begin{bmatrix}
m_{22}m_{33} – m_{23}m_{32} & m_{23}m_{31} – m_{21}m_{33} & m_{21}m_{32} – m_{22}m_{31} \\
m_{12}m_{32} – m_{12}m_{33} & m_{11}m_{33} – m_{13}m_{31} & m_{12}m_{31} – m_{11}m_{32} \\
m_{12}m_{23} – m_{13}m_{22} & m_{13}m_{21} – m_{11}m_{23} & m_{11}m_{22} – m_{12}m_{21}
\end{bmatrix}.$$
2.3 平移与仿射变换
我们已经学习了用矩阵$\mathbf{M}$变换向量的方法, 在2维空间中, 这些变换形式通常如下所示,$$x’ = m_{11}x + m_{12}y, \\ y’ = m_{21}x + m_{22}y.$$但上述变换形式仅能表示缩放与旋转, 无法表示平移. 特别地, 原点$(0, 0)$在线性变换下始终保持不动. 为了平移一个物体, 将其所有点均平移相同的量, 我们需要下述变换形式,$$x’ = x + x_t, \\ y’ = y + y_t.$$上述变换形式无法表示为一个$2 \times 2$的矩阵乘以一个列向量的形式. 在线性变换系统中加入平移的一种常见技巧为将一个独立的平移向量与一个变换矩阵组合起来, 其中, 变换矩阵仅负责处理缩放与旋转, 而向量则负责处理平移. 这是完全可行的, 但形式较为繁琐, 且组合这两个变换的规则并不像线性变换那样简单与干净.
$\\$ 相反地, 我们可以使用一个聪明的技巧让一个矩阵乘法同时做上述两个运算. 这个想法很简单: 用一个3维向量$(x, y, 1)^T$表示点$(x, y)$, 并使用$3 \times 3$的矩阵, 其形式如下所示$$\begin{bmatrix}
m_{11} & m_{12} & x_t \\
m_{21} & m_{22} & y_t \\
0 & 0 & 1
\end{bmatrix}.$$其中, 上述矩阵的第3行元素是固定的, 用于将1复制到变换后的向量中, 故变换后的所有向量的最后一个分量都为1, 且前2行计算向量的$x$分量, $y$分量与1的线性组合:$$\begin{bmatrix}
x’ \\
y’ \\
1
\end{bmatrix} = \begin{bmatrix}
m_{11} & m_{12} & x_t \\
m_{21} & m_{22} & y_t \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x \\
y \\
1
\end{bmatrix} = \begin{bmatrix}
m_{11}x + m_{12}y + x_t \\
m_{21}x + m_{22}y + y_t \\
1
\end{bmatrix}.$$由此可见, 上述式子中仅利用单个矩阵便实现了一个线性变换与一个平移变换的组合效果. 其对应的变换被称为仿射变换, 而为了实现仿射变换增加了一个额外维度的坐标被称为齐次坐标(Roberts, 1965; Riesenfeld, 1981; Penna & Patterson, 1986). 齐次坐标不仅简化了仿射变换的形式, 而且还简化了多个仿射变换的组合形式: 仅需将对应的矩阵相乘即可.
$\\$ 当我们需要变换表示方向的向量时, 上述形式便会出现问题——当我们平移一个物体时, 表示方向的向量不应该被改变. 为了解决这个问题, 我们可以将齐次坐标的第三个分量设为0:$$\begin{bmatrix}
1 & 0 & x_t \\
0 & 1 & y_t \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x \\
y \\
0
\end{bmatrix} = \begin{bmatrix}
x \\
y \\
0
\end{bmatrix}.$$齐次坐标可以被认为是一种处理平移变换的巧妙思想, 但亦有一种不同的几何解释. 注意到, 当我们基于笛卡尔坐标的$z$分量进行3D剪切时, 我们会得到这样的变换:$$\begin{bmatrix}
1 & 0 & x_t \\
0 & 1 & y_t \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x \\
y \\
z
\end{bmatrix} = \begin{bmatrix}
x + x_t z \\
y + y_t z \\
z
\end{bmatrix}.$$注意,上述变换结果包含了一般的2D变换形式, 但其中的$z$分量在2D中没有任何意义. 接下来我们为所有2D坐标添加分量$z = 1$, 则我们有$$\begin{bmatrix}
1 & 0 & x_t \\
0 & 1 & y_t \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x \\
y \\
1
\end{bmatrix} = \begin{bmatrix}
x + x_t \\
y + y_t \\
1
\end{bmatrix}.$$通过添加$(z = 1)$的分量得到2D坐标的齐次坐标, 我们现在可以将平移变换写为矩阵形式. 例如, 要在2D空间中将一个点平移$(t_x, t_y)$, 而后旋转角度$\phi$, 我们可使用变换矩阵$$\mathbf{M} = \begin{bmatrix}
cos \phi & -sin \phi & 0 \\
sin \phi & cos \phi & 0 \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0 & x_t \\
0 & 1 & y_t \\
0 & 0 & 1
\end{bmatrix}.$$注意到, 2D旋转矩阵为一个$3 \times 3$的矩阵, 其”平移槽” 中含有0. 这表明我们是使用沿$z = 1$的剪切变换来处理平移变换的. 我们可以将任意数量的2D剪切变换, 2D旋转变换与2D平移变换的组合表示为一个复合3D矩阵, 其最下面一行总为$(0, 0, 1)$, 故我们无需对此进行额外存储.
$\\$ 在3D空间中, 同样的技术亦可用于处理平移变换: 我们可以添加第4个分量从而得到一个齐次坐标, 然后我们进行平移:$$\begin{bmatrix}
1 & 0 & 0 & x_t \\
0 & 1 & 0 & y_t \\
0 & 0 & 1 & z_t \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix} = \begin{bmatrix}
x + x_t \\
y + y_t \\
z + z_t \\
1
\end{bmatrix}.$$类似地, 对于方向向量, 其第4个分量为0, 此时向量不受平移变换的影响.
示例(窗口变换). 在图形学中, 我们经常需要创建一个变换矩阵, 将矩形$[x_l, x_h] \times $$ [y_l, y_h]$中的点转换至矩形$[x_l’, x_h’] \times [y_l’, y_h’]$内. 这可以通过一次缩放变换与平移变换来完成. 不过, 更标准的做法是通过3次操作来创建这个变换:
$\\$ (1) 移动点$(x_l, y_l)$到原点.
$\\$ (2) 将矩形的大小缩放至与目标矩形相同.
$\\$ (3) 将原点移动到$(x_l’, y_l’)$.
$\\$ 当矩阵相乘时, 在最右边的矩阵是第一个与向量相乘的, 故我们可以用矩阵的语言将上述过程写为如下形式:$$windows = translate(x_l’, y_l’) \ scale(\frac{x_h’ – x_l’}{x_h – x_l}, \frac{y_h’ – y_l’}{y_h – y_l}) \ translate(-x_l, -y_l) \\ = \begin{bmatrix}
1 & 0 & x_l’ \\
0 & 1 & y_l’ \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
\frac{x_h’ – x_l’}{x_h – x_l} & 0 & 0 \\
0 & \frac{y_h’ – y_l’}{y_h – y_l} & 0 \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0 & -x_l \\
0 & 1 & -y_l \\
0 & 0 & 1
\end{bmatrix} \\ = \begin{bmatrix}
\frac{x_h’ – x_l’}{x_h – x_l} & 0 & \frac{x_l’ x_h – x_h’ x_l}{x_h – x_l} \\
0 & \frac{y_h’ – y_l’}{y_h – y_l} & \frac{y_l’ y_h – y_h’ y_l}{y_h – y_l} \\
0 & 0 & 1
\end{bmatrix}.$$类似地, 我们可以定义一个3D窗口变换, 将立方体$[x_l, x_h] \times [y_l, y_h] \times [z_l, z_h]$中的点转换至立方体$[x_l’, x_h’] \times [y_l’, y_h’] \times [z_l’, z_h’]$内:$$\begin{bmatrix}
\frac{x_h’ – x_l’}{x_h – x_l} & 0 & 0 & \frac{x_l’ x_h – x_h’ x_l}{x_h – x_l} \\
0 & \frac{y_h’ – y_l’}{y_h – y_l} & 0 & \frac{y_l’ y_h – y_h’ y_l}{y_h – y_l} \\
0 & 0 & \frac{z_h’ – z_l’}{z_h – z_l} & \frac{z_l’ z_h – z_h’ z_l}{z_h – z_l} \\
0 & 0 & 0 & 1
\end{bmatrix}.$$有趣的是, 若我们将一个由缩放变换, 剪切变换与旋转变换组成的任意矩阵与一个简单的平移矩阵相乘, 我们可得$$\begin{bmatrix}
1 & 0 & 0 & x_t \\
0 & 1 & 0 & y_t \\
0 & 0 & 1 & z_t \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
a_{11} & a_{12} & a_{13} & 0 \\
a_{21} & a_{22} & a_{23} & 0 \\
a_{31} & a_{32} & a_{33} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix} = \begin{bmatrix}
a_{11} & a_{12} & a_{13} & x_t \\
a_{21} & a_{22} & a_{23} & y_t \\
a_{31} & a_{32} & a_{33} & z_t \\
0 & 0 & 0 & 1
\end{bmatrix}.$$因此, 我们可以把任意变换矩阵彻底分解为缩放/旋转部分与平移部分. 一类重要的变换便是刚体变换. 它们仅由平移变换与旋转变换组成, 不对变换对象进行拉伸或收缩.
2.4 变换矩阵的逆矩阵
我们可以使用SVD对矩阵进行求逆. 由于任意矩阵均可以分解为一个旋转矩阵乘以一个缩放矩阵再乘以一个旋转矩阵的形式, 故求逆就变得十分简单. 例如, 在3D空间中我们有$$\mathbf{M} = \mathbf{R}_1 \ scale(\sigma_1, \sigma_2, \sigma_3) \ \mathbf{R}_2,$$易知,$$\mathbf{M}^{-1} = \mathbf{R}_2^T \ scale(1 / \sigma_1, 1 / \sigma_2, 1 / \sigma_3) \ \mathbf{R}_1^T.$$
2.5 坐标变换
当我们在计算机中存储或使用向量前, 我们必须声明向量所在的坐标系. 从几何上讲, 一个2维坐标系由一个原点与一组基(一个2维向量构成的集合) 组成. 我们通常假设这组基是一组标准正交基, 当选定的坐标系为笛卡尔坐标系, 即原点为$\mathbf{o}$, 基为$\{ \mathbf{x}, \mathbf{y}\}$时, 2维空间中一个点$\mathbf{p}$可由坐标$(x_\mathbf{p}, y_\mathbf{p})$描述, 即$$\mathbf{p} = (x_\mathbf{p}, y_\mathbf{p}) \equiv \mathbf{o} + x_\mathbf{p} \mathbf{x} + y_\mathbf{p} \mathbf{y}.$$当选定的坐标系的原点为$\mathbf{e}$, 基为$\{ \mathbf{u}, \mathbf{v}\}$时, 2维空间中一个点$\mathbf{p}$可由坐标$(u_\mathbf{p}, $$ v_\mathbf{p})$描述, 即$$p = (u_\mathbf{p}, v_\mathbf{p}) \equiv \mathbf{e} + u_\mathbf{p} \mathbf{u} + v_\mathbf{p} \mathbf{v}.$$我们可以用矩阵的语言来描述上述两个坐标之间的关系, 如下所示:$$\begin{bmatrix}
x_\mathbf{p} \\
y_\mathbf{p} \\
1
\end{bmatrix} = \begin{bmatrix}
1 & 0 & x_\mathbf{e} \\
0 & 1 & y_\mathbf{e} \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x_\mathbf{u} & x_\mathbf{v} & 0 \\
y_\mathbf{u} & y_\mathbf{v} & 0 \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
u_\mathbf{p} \\
v_\mathbf{p} \\
1
\end{bmatrix} = \begin{bmatrix}
x_\mathbf{u} & x_\mathbf{v} & x_\mathbf{e} \\
y_\mathbf{u} & y_\mathbf{v} & y_\mathbf{e} \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
u_\mathbf{p} \\
v_\mathbf{p} \\
1
\end{bmatrix}.$$我们可将上式简记为$$\mathbf{p}_{xy} = \begin{bmatrix}
\mathbf{u} & \mathbf{v} & \mathbf{e} \\
0 & 0 & 1
\end{bmatrix} \mathbf{p}_{uv}.$$上式中的变换矩阵将点$\mathbf{p}$由自定义的坐标系转换至笛卡尔坐标系下. 反过来, 我们有$$\begin{bmatrix}
u_\mathbf{p} \\
v_\mathbf{p} \\
1
\end{bmatrix} = \begin{bmatrix}
x_\mathbf{u} & y_\mathbf{u} & 0 \\
x_\mathbf{v} & y_\mathbf{v} & 0 \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0 & -x_\mathbf{e} \\
0 & 1 & -y_\mathbf{e} \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x_\mathbf{p} \\
y_\mathbf{p} \\
1
\end{bmatrix}.$$我们可将上式简记为$$\mathbf{p}_{uv} = \begin{bmatrix}
\mathbf{u} & \mathbf{v} & \mathbf{e} \\
0 & 0 & 1
\end{bmatrix}^{-1} \mathbf{p}_{xy}.$$类似地, 我们可得3维空间中不同坐标系下的坐标之间的关系,$$\begin{bmatrix}
x_\mathbf{p} \\
y_\mathbf{p} \\
z_\mathbf{p} \\
1
\end{bmatrix} = \begin{bmatrix}
1 & 0 & 0 & x_\mathbf{e} \\
0 & 1 & 0 & y_\mathbf{e} \\
0 & 0 & 1 & z_\mathbf{e} \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x_\mathbf{u} & x_\mathbf{v} & x_\mathbf{w} & 0 \\
y_\mathbf{u} & y_\mathbf{v} & y_\mathbf{w} & 0 \\
z_\mathbf{u} & z_\mathbf{v} & z_\mathbf{w} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
u_\mathbf{p} \\
v_\mathbf{p} \\
w_\mathbf{p} \\
1
\end{bmatrix}, \\ \mathbf{p}_{xyz} = \begin{bmatrix}
\mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e} \\
0 & 0 & 0 & 1
\end{bmatrix} \mathbf{p}_{uvw},$$反过来, 我们有$$\begin{bmatrix}
u_\mathbf{p} \\
v_\mathbf{p} \\
w_\mathbf{p} \\
1
\end{bmatrix} = \begin{bmatrix}
x_\mathbf{u} & y_\mathbf{u} & z_\mathbf{u} & 0 \\
x_\mathbf{v} & y_\mathbf{v} & z_\mathbf{v} & 0 \\
x_\mathbf{w} & y_\mathbf{w} & z_\mathbf{w} & 0 \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0 & 0 & -x_\mathbf{e} \\
0 & 1 & 0 & -y_\mathbf{e} \\
0 & 0 & 1 & -z_\mathbf{e} \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x_\mathbf{p} \\
y_\mathbf{p} \\
z_\mathbf{p} \\
1
\end{bmatrix}, \\ \mathbf{p}_{uvw} = \begin{bmatrix}
\mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e} \\
0 & 0 & 0 & 1
\end{bmatrix}^{-1} \mathbf{p}_{xyz}.$$
3. 常见问题
问1: 能否不使用矩阵进行变换?
$\\$ 答1: 可以的, 但是在实际使用中将更难推导, 更难调试, 且效率也不会提高. 此外, 所有现代的图形API均使用矩阵进行变换, 因此为了能够更好地掌握各种图形API, 我们必须理解变换矩阵.
问2: 变换矩阵的最后一行总是$(0, 0, 0, 1)$, 必须将其保存吗?
$\\$ 答2: 除非进行透视变换, 否则无需进行额外存储.
4. 相关习题
4.1 写出在3维空间中将一点移动$(x_m, y_m, z_m)$的$4 \times 4$的3维矩阵.
$\\$ 解: $\begin{bmatrix}
1 & 0 & 0 & x_m \\
0 & 1 & 0 & y_m \\
0 & 0 & 1 & z_m \\
0 & 0 & 0 & 1
\end{bmatrix}$.
4.2 写出绕$y$轴旋转角度$\theta$的$4 \times 4$的3维矩阵.
$\\$ 解: $\begin{bmatrix}
cos \theta & 0 & sin \theta & 0 \\
0 & 1 & 0 & 0 \\
-sin \theta & 0 & cos \theta & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}$.
4.3 写出在所有方向上缩放50%的$4 \times 4$的3维矩阵.
$\\$ 解: $\begin{bmatrix}
0.5 & 0 & 0 & 0 \\
0 & 0.5 & 0 & 0 \\
0 & 0 & 0.5 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}$.
4.4 写出顺时针旋转90度的2维旋转矩阵.
$\\$ 解: $\begin{bmatrix}
cos \frac{\pi}{2} & sin \frac{\pi}{2} \\
-sin \frac{\pi}{2} & cos \frac{\pi}{2}
\end{bmatrix} = \begin{bmatrix}
0 & 1 \\
-1 & 0
\end{bmatrix}.$
4.5 将4.4中的矩阵写为3个剪切矩阵的乘积.
$\\$ 解: 由旋转矩阵的Paeth分解可得$$\begin{bmatrix}
0 & 1 \\
-1 & 0
\end{bmatrix} = \begin{bmatrix}
cos \frac{\pi}{2} & sin \frac{\pi}{2} \\
-sin \frac{\pi}{2} & cos \frac{\pi}{2}
\end{bmatrix} \\ = \begin{bmatrix}
1 & \frac{cos\phi – 1}{sin\phi}\\
0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0\\
sin\phi & 1
\end{bmatrix} \begin{bmatrix}
1 & \frac{cos\phi – 1}{sin\phi}\\
0 & 1
\end{bmatrix} \\ = \begin{bmatrix}
1 & -1\\
0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0\\
1 & 1
\end{bmatrix} \begin{bmatrix}
1 & -1\\
0 & 1
\end{bmatrix}.$$
4.6 计算下述刚体变换矩阵的逆矩阵:$$\begin{bmatrix}
\mathbf{R} & \mathbf{t} \\
0 \ 0 \ 0 & 1
\end{bmatrix},$$其中, $\mathbf{R}$为一个$3 \times 3$的旋转矩阵, $\mathbf{t}$为一个3维向量.
$\\$ 解: $\begin{bmatrix}
\mathbf{R}^T & -\mathbf{t} \\
0 \ 0 \ 0 & 1
\end{bmatrix}$.
4.7 证明一个仿射变换的矩阵(最后一行的非零元为最后一个元素, 且为1) 的逆矩阵亦具有相同的形式.
$\\$ 解: 一个仿射变换$T: \mathbb{R}^n \mapsto \mathbb{R}^n$可以写为:$$T(\mathbf{x}) = \mathbf{A} \mathbf{x} + \mathbf{b},$$其中, $\mathbf{x}$, $\mathbf{b} \in \mathbb{R}^n$, $\mathbf{A}$为一个$n \times n$的矩阵. 通过矩阵$\mathbf{A}$的增广矩阵, 我们可以得到一个变换$T’: \mathbb{R}^{n + 1} \mapsto \mathbb{R}^{n + 1}$:$$T'(\mathbf{y}) = \mathbf{A}’ \mathbf{y},$$其中, $\mathbf{A}’ = \begin{bmatrix}
\mathbf{A} & \mathbf{b} \\
\mathbf{0} & 1
\end{bmatrix}$, $\mathbf{y} = \begin{bmatrix}
\mathbf{x} & 1
\end{bmatrix}^T$, $\mathbf{0}$为一个$1 \times n$的零向量.
$\\$ 接下来, 不妨令$T(\mathbf{x}) = \mathbf{z}$, 则$\mathbf{z} – \mathbf{b} = \mathbf{A} \mathbf{x}$. 若$\mathbf{A}^{-1}$存在(由仿射变换定义可知, 仿射变换为一个双射, 故必存在逆变换, 完整定义详见参考材料2), 我们有$$\mathbf{x} = \mathbf{A}^{-1}(\mathbf{z} – \mathbf{b}) = \mathbf{A}^{-1} \mathbf{z} – \mathbf{A}^{-1} \mathbf{b},$$上式可以改写为$$\mathbf{x} = \mathbf{A}^{-1} \mathbf{z} + \mathbf{b}’,$$其中, $\mathbf{b}’ = -\mathbf{A}^{-1} \mathbf{b}$. 这意味着仿射变换$T$的逆变换$T^{-1}$亦为一个仿射变换, 且其对应的增广矩阵的分块矩阵形式如下所示:$$(\mathbf{A}^{-1})’ = \begin{bmatrix}
\mathbf{A}^{-1} & -\mathbf{A}^{-1} \mathbf{b} \\
\mathbf{0} & 1
\end{bmatrix}.$$综上所述, 命题得证. 必要时可验证$\mathbf{A}’ (\mathbf{A}^{-1})’ = (\mathbf{A}^{-1})’ \mathbf{A}’ = \mathbf{I}_{n + 1}$.
4.8 描述下述2维变换矩阵的作用:$$\begin{bmatrix}
0 & -1 & 1 \\
1 & 0 & 1 \\
0 & 0 & 1
\end{bmatrix}.$$解: 首先将作用对象逆时针旋转90度, 再将作用对象平移$(1, 1)$.
4.9 写出将一个2维点$\mathbf{x}$绕点$\mathbf{p} = (x_\mathbf{p}, y_\mathbf{p})$旋转角度$\theta$的$3 \times 3$的矩阵.
$\\$ 解: 通过3次操作来创建这个变换:
$\\$ (1) 将点$\mathbf{x}$与点$\mathbf{p} = (x_\mathbf{p}, y_\mathbf{p})$进行平移, 使得点$\mathbf{p}$与原点重合.
$\\$ (2) 将平移后的点$\mathbf{x}$绕原点旋转角度$\theta$.
$\\$ (3) 将旋转后的点$\mathbf{x}$与平移后的点$\mathbf{p}$再次进行平移, 使得点$\mathbf{p}$回到原来的位置.
$\\$ 当矩阵相乘时, 在最右边的矩阵是第一个与向量相乘的, 故我们可以用矩阵的语言将上述过程写为如下形式:$$translate(x_\mathbf{p}, y_\mathbf{p}) \ rotate(\frac{\pi}{2}) \ translate(-x_\mathbf{p}, -y_\mathbf{p}) \\ = \begin{bmatrix}
1 & 0 & x_\mathbf{p} \\
0 & 1 & y_\mathbf{p} \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
cos \frac{\pi}{2} & -sin \frac{\pi}{2} & 0 \\
sin \frac{\pi}{2} & cos \frac{\pi}{2} & 0 \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0 & -x_\mathbf{p} \\
0 & 1 & -y_\mathbf{p} \\
0 & 0 & 1
\end{bmatrix}.$$
4.10 写出一个$4 \times 4$的旋转矩阵, 它将一组3维正交向量$$\mathbf{u} = (x_\mathbf{u}, y_\mathbf{u}, z_\mathbf{u})^T, \\ \mathbf{v} = (x_\mathbf{v}, y_\mathbf{v}, z_\mathbf{v})^T, \\ \mathbf{w} = (x_\mathbf{w}, y_\mathbf{w}, z_\mathbf{w})^T$$变换为另外一组3维正交向量$$\mathbf{a} = (x_a, y_a, z_a)^T, \\ \mathbf{b} = (x_b, y_b, z_b)^T, \\ \mathbf{c} = (x_c, y_c, z_c)^T,$$即$\mathbf{M} \mathbf{u} = \mathbf{a}$, $\mathbf{M} \mathbf{v} = \mathbf{b}$, 且$\mathbf{M} \mathbf{w} = \mathbf{c}$.
$\\$ 解: 易知$\mathbf{M} \begin{bmatrix}
\mathbf{u} & \mathbf{v} & \mathbf{w}
\end{bmatrix} = \begin{bmatrix}
\mathbf{a} & \mathbf{b} & \mathbf{c}
\end{bmatrix}$, 且$\begin{bmatrix}
\mathbf{u} & \mathbf{v} & \mathbf{w}
\end{bmatrix}$是可逆的, 故$$\mathbf{M} = \begin{bmatrix}
\mathbf{a} & \mathbf{b} & \mathbf{c}
\end{bmatrix} \begin{bmatrix}
\mathbf{u} & \mathbf{v} & \mathbf{w}
\end{bmatrix}^{-1}.$$
4.11 4.10答案中的逆矩阵是什么?
$\\$ 解: 由$\mathbf{A}^{-1} = \frac{\mathbf{A}^*}{|\mathbf{A}|}$可得$$\begin{bmatrix}
\mathbf{u} & \mathbf{v} & \mathbf{w}
\end{bmatrix}^{-1} = \frac{\begin{bmatrix}
y_\mathbf{v} z_\mathbf{w} – y_\mathbf{w} z_\mathbf{v} & x_\mathbf{w} z_\mathbf{v} – x_\mathbf{v} z_\mathbf{w} & x_\mathbf{v} y_\mathbf{w} – x_\mathbf{w} y_\mathbf{v} \\
y_\mathbf{w} z_\mathbf{u} – y_\mathbf{w} z_\mathbf{v} & x_\mathbf{u} z_\mathbf{w} – x_\mathbf{w} z_\mathbf{u} & y_\mathbf{u} x_\mathbf{w} – x_\mathbf{u} y_\mathbf{w} \\
y_\mathbf{u} z_\mathbf{v} – y_\mathbf{v} z_\mathbf{u} & x_\mathbf{v} z_\mathbf{u} – x_\mathbf{u} z_\mathbf{v} & x_\mathbf{u} y_\mathbf{v} – y_\mathbf{u} x_\mathbf{v} \\
\end{bmatrix}}{x_\mathbf{u}(y_\mathbf{v} z_\mathbf{w} – y_\mathbf{w} z_\mathbf{v}) – y_\mathbf{u}(x_\mathbf{v} z_\mathbf{w} – x_\mathbf{w} z_\mathbf{v}) + z_\mathbf{u}(x_\mathbf{v} y_\mathbf{w} – x_\mathbf{w} y_\mathbf{v})}.$$