实在是惭愧, 最近几周实在是有点忙(主要因为周末也过宁波了……), 导致也挺久没更新博客了. 本来想着今天继续写一下博客, 但由于最近在移植UE5的modeling模式的QEM算法, 有些自己实现的细节仍旧存在Bug, 使得我一直难以释怀, 因此决定今天继续鸽博客(逃ε=ε=ε=┏(゜ロ゜;)┛), 转而继续研究QEM算法的实现细节~ 今天就先开个坑, 日后一定补上!(没错, 就是酱紫!)
参考材料
1. 计算机图形学笔记——视图(viewing)
2. preserving z-values during projection?
3. 图形学坐标变换3. 投影变换-透视投影矩阵到Clip空间
1. Viewing变换
1.1 视口变换
视口变换将一个轴对齐的矩形映射到另一个矩形, 其变换过程如下所示:$$\begin{bmatrix}
x_{screen} \\
y_{screen} \\
1
\end{bmatrix} = \begin{bmatrix}
\frac{n_x}{2} & 0 & \frac{n_x – 1}{2}\\
0 & \frac{n_y}{2} & \frac{n_y – 1}{2}\\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x_{canonical} \\
y_{canonical} \\
1
\end{bmatrix}.$$上述矩阵忽略了Canonical View Volume(一个中心位于原点, 边长为2的立方体) 中点的$z$分量, 因为点与投影面之间沿着投影方向的距离并不会影响该点在图像中的投影位置. 但我们依旧往上述矩阵中添加了一行与一列来得到一个完整的视口矩阵(如下所示), 该矩阵并不会改变点的$z$分量. 最终我们会需要投影点的$z$分量, 因为它可用于Z-Buffer剔除.$$\mathbf{M}_{vp} = \begin{bmatrix}
\frac{n_x}{2} & 0 & 0 & \frac{n_x – 1}{2} \\
0 & \frac{n_y}{2} & 0 & \frac{n_y – 1}{2} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}.$$
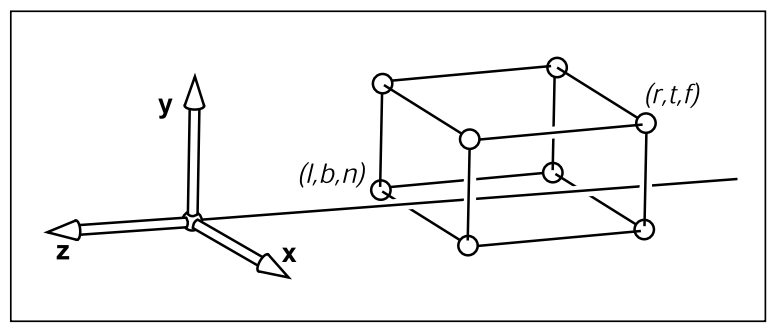
1.2 正交投影
Orthographic View Volume是沿着负$z$轴的, 且$f < n < 0$, 如下图所示. 从Orthographic View Volume到Canonical View Volume的变换为另一个窗口变换, 易得该变换对应的矩阵为:$$\mathbf{M}_{orh} = \begin{bmatrix}
\frac{2}{r - l} & 0 & 0 & -\frac{r + l}{r - l} \\
0 & \frac{2}{t - b} & 0 & -\frac{t + b}{t - b} \\
0 & 0 & \frac{2}{n - f} & -\frac{n + f}{n - f} \\
0 & 0 & 0 & 1
\end{bmatrix}.$$
为了在Orthographic View Volume中绘制3D线段, 我们将线段投影到屏幕上, 其投影点的位置与$z$分量无关, 其投影过程如下所示:$$\begin{bmatrix}
x_{pixel} \\
y_{pixel} \\
z_{canonical} \\
1
\end{bmatrix} = (\mathbf{M}_{vp} \mathbf{M}_{orh})\begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}.$$
1.3 相机变换
不妨设$\mathbf{e}$为视点的位置, $\mathbf{g}$为视线的方向向量, $\mathbf{t}$为竖直向上的方向向量, 这些向量为我们提供了足够的信息来建立一个以$\mathbf{e}$为原点, 以$\mathbf{u}$, $\mathbf{v}$与$\mathbf{w}$为基的相机坐标系, 其中, $\mathbf{u}$, $\mathbf{v}$与$\mathbf{w}$的定义如下所示:$$\mathbf{w} = -\frac{\mathbf{g}}{\left \| \mathbf{g} \right \| }, \\ \mathbf{u} = \frac{\mathbf{t} \times \mathbf{w}}{\left \| \mathbf{t} \times \mathbf{w} \right \| }, \\ \mathbf{v} = \mathbf{w} \times \mathbf{u}.$$一般来说, 模型的坐标是在局部坐标系下的, 为了绘制3D线段, 我们需要将线段端点的坐标从局部坐标系下变换到相机坐标系下, 执行这种变换的矩阵如下所示:$$\mathbf{M}_{cam} = \begin{bmatrix}
\mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e} \\
0 & 0 & 0 & 1
\end{bmatrix}^{-1} = \begin{bmatrix}
x_u & y_u & z_u & 0 \\
x_v & y_v & z_v & 0 \\
x_w & y_w & z_w & 0 \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
1 & 0 & 0 & -x_\mathbf{e} \\
0 & 1 & 0 & -y_\mathbf{e} \\
0 & 0 & 1 & -z_\mathbf{e} \\
0 & 0 & 0 & 1
\end{bmatrix}.$$我们亦可以把这种变换视为一个先把视点$\mathbf{e}$移到局部坐标系原点, 然后把基$\mathbf{u}$, $\mathbf{v}$与$\mathbf{w}$分别变换到$x$轴上, $y$轴上与$z$轴上的过程.
2. 投影变换
1维透视投影的关键特点是, 屏幕上物体的大小与其$z$分量的倒数$1/z$成正比, 如下所示:$$y_s = \frac{d}{z}y,$$其中, 各符号的定义如下图所示.
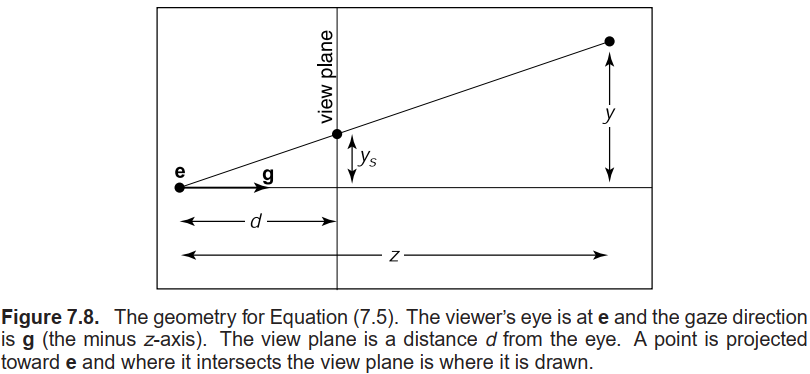
而在2维透视投影中(即更常见的渲染流程), 我们需要在仿射变换后进行齐次除法. 我们已经约定利用齐次坐标$\begin{bmatrix}
x & y & z & 1
\end{bmatrix}^T$表示点$(x, $$ y, z)$, 其额外的$w$分量总为1, 这是通过将$\begin{bmatrix}
0 & 0 & 0 & 1
\end{bmatrix}$作为仿射变换矩阵的第4行来保证的.
$\\$ 接下来, 我们扩展上述约定: 齐次坐标$\begin{bmatrix}
x & y & z & w
\end{bmatrix}^T$表示点$(x / w, $$ y / w, z / $$ w)$. 当$w = 1$时, 这与上述情形并无区别, 但当仿射变换矩阵的第4行不为$\begin{bmatrix}
0 & 0 & 0 & 1
\end{bmatrix}$时, 则可以实现更多可能的变换, 从而使得最终计算得到的$w$的值不为1.
$\\$ 具体来说, 线性变换允许计算下述形式的表达式$$x’ = ax + by + cz,$$而仿射变换则将可计算的表达式形式扩展为如下形式$$x’ = ax + by + cz + d.$$将$w$作为分母, 能将可计算的表达式形式进一步地扩展为如下形式$$x’ = \frac{ax + by + cz + d}{ex + fy + gz + h};$$上述函数可被称为关于$x$, $y$与$z$的”线性有理函数”. 然而需要满足一个额外的约束, 即对于变换的作用点的所有分量的分母是相同的:$$x’ = \frac{a_1 x + b_1 y + c_1 z + d_1}{ex + fy + gz + h}, \\ y’ = \frac{a_2 x + b_2 y + c_2 z + d_2}{ex + fy + gz + h}, \\ z’ = \frac{a_3 x + b_3 y + c_3 z + d_3}{ex + fy + gz + h}.$$用矩阵变换的语言可将上式写为$$\begin{bmatrix}
\widetilde{x} \\
\widetilde{y} \\
\widetilde{z} \\
\widetilde{w}
\end{bmatrix} = \begin{bmatrix}
a_1 & b_1 & c_1 & d_1 \\
a_2 & b_2 & c_2 & d_2 \\
a_3 & b_3 & c_3 & d_3 \\
e & f & g & h
\end{bmatrix} \begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}, \\ (x’, y’, z’) = (\widetilde{x} / \widetilde{w}, \widetilde{y} / \widetilde{w}, \widetilde{z} / \widetilde{w}).$$这样的变换被称为射影变换或单应性变换.
$\\$ 有一种更优雅的方式来表达同样的思想, 它避免了对$w$分量的特殊处理. 在这种观点下, 一个3维投影变换即为一个简单的4维线性变换, 需要满足的约束条件为呈倍数关系的齐次坐标均是等价的:$$\mathbf{x} \sim \alpha \mathbf{x}, \forall \alpha \ne 0,$$其中, $\mathbf{x}$为一个齐次坐标, 符号$\sim$表示”等价于”, 上式表示两个呈倍数关系的齐次坐标均描述了3维空间中的同一点.
3. 透视投影
射影变换的机制使得实现透视投影所需的除以$z$分量的操作变得简单. 在图7.8所示的1维透视投影特点的例子中, 我们可以使用如下矩阵变换来实现透视投影:$$\begin{bmatrix}
y_s \\
1
\end{bmatrix} \sim \begin{bmatrix}
d & 0 & 0 \\
0 & 1 & 0
\end{bmatrix} \begin{bmatrix}
y \\
z \\
1
\end{bmatrix}.$$上述矩阵将2维齐次坐标$\begin{bmatrix}
y; & z; & 1
\end{bmatrix}^T$变换为1维齐次坐标$\begin{bmatrix}
dy & z
\end{bmatrix}^T$, 它表示1维点$(dy / z)$.
$\\$ 对于3D空间中的透视投影矩阵, 我们将采用通常的约定, 即相机位于原点且面朝$−z$轴的方向, 故视锥体内的点$(0, 0, z)$与相机的距离为$−z$. 与正交投影一样, 我们亦采用了远近平面的概念, 这限制了可视范围. 此处, 我们将使用近平面作为投影平面, 故投影平面与相机的距离为$-n$.
$\\$ 因此, 所需的映射为$y_s = (n / z)y$, 同理可得$x_s = (n / z)x$. 这种变换可以通过下述的透视变换矩阵(需要区别于透视投影矩阵) 实现:$$\mathbf{P} = \begin{bmatrix}
n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n + f & -fn \\
0 & 0 & 1 & 0
\end{bmatrix}.$$通过上述透视投影矩阵的第1行, 第2行与第4行, 我们可以实现简单的透视变换, 与正交矩阵, 视口矩阵类似, 第3行是为了引入待变换点的坐标的$z$分量, 以此用于Z-Buffer剔除. 然而, 在透视投影中, 非常量分母使得待变换点的原本坐标的$z$分量的还原变得十分困难. 实际上, 在这过程中, 我们几乎不可能阻止待变换点的坐标的$z$分量的改变. 但退一步地, 我们可以选择仅保持近平面上或远平面上的点的坐标的$z$分量不变.
$\\$ 有许多矩阵可以作为透视变换矩阵, 它们都对待变换点的坐标的$z$分量进行了非线性”扭曲”. 这类特定的矩阵具有良好的特性: 它们能够将$(z $$ = n)$-平面上的点与$(z = f)$-平面上的点依旧保持在各自所在的平面上(其坐标的$x$分量与$y$分量均经过了适当调整). 透视变换矩阵$\mathbf{P}$对点$(x, y, z)$的变换过程为$$\mathbf{P} \begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix} = \begin{bmatrix}
x \\
y \\
z \frac{n + f}{n} – f \\
\frac{z}{n}
\end{bmatrix} \sim \begin{bmatrix}
\frac{nx}{z} \\
\frac{ny}{z} \\
n + f – \frac{fn}{z} \\
1
\end{bmatrix}.$$有时我们想要计算透视变换矩阵$\mathbf{P}$的逆矩阵, 例如当欲根据屏幕空间下的带有$z$分量的坐标计算原始空间下的坐标时. 其逆矩阵为$$\mathbf{P}^{-1} = \begin{bmatrix}
\frac{1}{n} & 0 & 0 & 0 \\
0 & \frac{1}{n} & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & -\frac{1}{fn} & -\frac{n + f}{fn}
\end{bmatrix}.$$由于一个齐次坐标乘以一个标量并不会改变所表示的笛卡尔坐标, 故对于作用于齐次坐标的变换矩阵亦是如此. 我们可以通过乘以$nf$把逆矩阵写成更漂亮的形式:$$\mathbf{P}^{-1} = \begin{bmatrix}
f & 0 & 0 & 0 \\
0 & f & 0 & 0 \\
0 & 0 & 0 & fn \\
0 & 0 & -1 & n + f
\end{bmatrix}.$$以正交投影矩阵$\mathbf{M}_{orth}$为例, 它将Perspective View Volume(形状类似于金字塔的切片或视锥体) 映射到Orthographic View Volume(轴对齐的立方体). 透视变换矩阵$\mathbf{P}$的美妙之处在于, 它可以结合正交投影矩阵来获得Canonical View Volume, 即$$\mathbf{M}_{per} = \mathbf{M}_{orh} \mathbf{P}.$$而我们所添加的只是一个矩阵与除以$w$分量的操作. 更重要的是, 我们可以充分利用$4 \times 4$的透视变换矩阵$\mathbf{P}$的最后一行.
$\\$ 然而, 有一个问题是: 如何计算透视投影矩阵$\mathbf{M}_{per}$中的$l$, $r$, $b$与$t$? 它们确定了我们观看的”窗口”. 由于透视投影矩阵并不会改变$(z = n)$平面上的点的坐标的$x$分量与$y$分量, 因此我们可以在该平面上计算$(l, r, b, $$ t)$.
$\\$ 为了将透视变换矩阵$\mathbf{P}$整合到我们的正交投影流程中, 我们仅需将透视投影矩阵$\mathbf{M}_{per}$替换为正交投影矩阵$\mathbf{M}_{orh}$, 即在应用相机变换矩阵$\mathbf{M}_{cam}$之后, 正交投影矩阵$\mathbf{M}_{orh}$之前应用透视变换矩阵$\mathbf{P}$. 综上所述, 透视变换的完整流程如下所示,$$\mathbf{M} = \mathbf{M}_{vp} \mathbf{M}_{orh} \mathbf{P} \mathbf{M}_{cam},$$其中, 透视投影矩阵$\mathbf{M}_{per} = \mathbf{M}_{orh} \mathbf{P}$的形式如下所示:$$\mathbf{M}_{per} = \begin{bmatrix}
\frac{2n}{r- l} & 0 & \frac{l + r}{l – r} & 0 \\
0 & \frac{2n}{t – b} & \frac{b + t}{b – t} & 0 \\
0 & 0 & \frac{f + n}{n – f} & \frac{2fn}{f – n} \\
0 & 0 & 1 & 0
\end{bmatrix}.$$类似的矩阵经常出现在文献中, 但它们通常仅是几个简单矩阵的乘积, 并非想象中的如此难以理解.
4. 透视变换的一些性质
透视变换的一个重要性质便是它将直线变换为直线, 将平面变换为平面. 此外, 它将View Volume中的线段变换为Canonical Volume中的线段. 为了理解这一点, 考虑线段$$\mathbf{q} + t(\mathbf{Q} – \mathbf{q}).$$当用一个$4 \times 4$的矩阵$\mathbf{M}$对上述线段上的点进行变换时, 我们可得一个齐次坐标可能变化的点:$$\mathbf{M} \mathbf{q} + t(\mathbf{M} \mathbf{Q} – \mathbf{M} \mathbf{q}) \equiv \mathbf{r} + t(\mathbf{R} – \mathbf{r}).$$经变换后的线段上的点的齐次坐标为$$\frac{\mathbf{r} + t(\mathbf{R} – \mathbf{r})}{w_\mathbf{r} + t(w_\mathbf{R} – w_\mathbf{r})}.$$若上式可写为如下形式$$\frac{\mathbf{r}}{w_\mathbf{r}} + f(t)(\frac{\mathbf{R}}{w_\mathbf{R}} – \frac{\mathbf{r}}{w_\mathbf{r}}),$$则所有的经变换后的线段上的点均位于一条3D直线上.易知, 令$$f(t) = \frac{w_\mathbf{R} t}{w_\mathbf{r} + t(w_\mathbf{R} – w_\mathbf{r})}$$即可满足要求.
5. 视野(Field-of-View, 简称FOV)
虽然我们可以使用$(l, r, b, t)$与$n$定义任意窗口, 但有时我们希望有一个更简单的系统, 在该系统下相机位于窗口中心, 且朝向屏幕外, 这意味着需要增加如下约束:$$l = -r, \\ b = -t.$$若我们还加上像素形状为正方形的约束, 即图像禁止出现形状畸变的问题, 那么$r$与$t$的比值必须等于水平方向上的像素数量与竖直方向上的像素数量的比值:$$\frac{n_x}{n_y} = \frac{r}{t}.$$一旦指定了水平方向上的像素数量$n_x$与竖直方向上的像素数量$n_y$, 则仅剩下一个自由度, 我们通常使用FOV $\theta$来设置, 如下图所示.
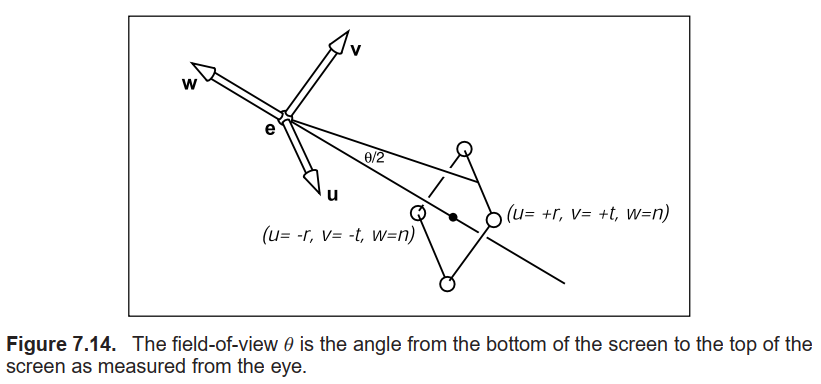
$\theta$有时亦被称为竖直方向上的FOV, 以区别于左右两边的夹角或对角之间的夹角. 从图中我们可以看到$$tan \frac{\theta}{2} = \frac{t}{|n|}.$$若$n$与竖直方向上的FOV $\theta$是确定的, 那么我们可得$t$. 一般来说, $n$的值是固定的, 如此一来, 定义窗口的自由度也便少了一个.
6. 常见问题
问1: 正交投影在实践中有用吗?
$\\$ 答1: 正交投影在需要进行相对长度判断的应用场景中十分有用. 此外, 它还可以简化某些医学可视化应用程序中透视投影开销过于昂贵的部分.
问2: 在透视视图中绘制的细分球体看起来像一个椭球体, 这是一个Bug吗?
$\\$ 答2: 这是正确的. 若把视点放置于相机处, 则细分球体看起来便像一个椭球体.
问3: 透视变换矩阵是否会改变待变换点的坐标的$z$分量的符号? 若是的话, 这种性质是否会产生问题呢?
$\\$ 答3: 不一定. 经变换后的点的坐标的$z$分量为$$z’ = n + f – \frac{fn}{z}.$$故可以确定的是, 当$z = + \epsilon$时, $z’ = -\infty$; 而当$z = – \epsilon$时, $z’ = \infty$. 因此, 尽管所有3D点都将被投射到屏幕空间上, 但任意含坐标的$z$分量为0的点的线段都将被”撕裂”(跳跃间断点). 对于Viewing Volume(其所有端点的坐标的$z$分量构成的区间不包含0) 内的待变换点, 是不会产生”撕裂” 现象的. 而对于Viewing Volume外的点, 则需要进行裁剪. 换句话说, “撕裂” 现象使裁剪本身变得更加复杂.
问4: 透视变换矩阵改变齐次坐标的$w$分量, 这是否会使得平移变换与缩放变换不再正常工作?
$\\$ 答4: 将一个平移变换矩阵作用于齐次坐标上, 我们可得$$\begin{bmatrix}
1 & 0 & 0 & t_x \\
0 & 1 & 0 & t_y \\
0 & 0 & 1 & t_z \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
hx \\
hy \\
hz \\
h
\end{bmatrix} = \begin{bmatrix}
hx + ht_x \\
hy + ht_y \\
hz + ht_z \\
h
\end{bmatrix} \xrightarrow[]{homogenize} \begin{bmatrix}
x + t_x \\
y + t_y \\
z + t_z \\
1
\end{bmatrix}.$$同理可知, 当一个缩放变换矩阵作用于齐次坐标上时, 亦可正常工作.
7. 相关习题
7.1 构建一个视口变换矩阵, 其作用的像素坐标的$y$分量是从图像自顶向下递增的.
$\\$ 解: 将原视口变换矩阵$\mathbf{M}_{vp}$中的$n_y$替换为$1 – n_y$即可得$$\mathbf{M}_{vp}’ = \begin{bmatrix}
\frac{n_x}{2} & 0 & 0 & \frac{n_x – 1}{2} \\
0 & \frac{1 – n_y}{2} & 0 & \frac{-n_y}{2} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}.$$
7.2 将正交投影矩阵与视口变换矩阵相乘.
$\\$ 解: 易知, 视口变换矩阵为$$\mathbf{M}_{vp} = \begin{bmatrix}
\frac{n_x}{2} & 0 & 0 & \frac{n_x – 1}{2} \\
0 & \frac{n_y}{2} & 0 & \frac{n_y – 1}{2} \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix},$$正交投影矩阵为$$\mathbf{M}_{orh} = \begin{bmatrix}
\frac{2}{r – l} & 0 & 0 & -\frac{r + l}{r – l} \\
0 & \frac{2}{t – b} & 0 & -\frac{t + b}{t – b} \\
0 & 0 & \frac{2}{n – f} & -\frac{n + f}{n – f} \\
0 & 0 & 0 & 1
\end{bmatrix},$$将上述两个矩阵相乘可得,$$\mathbf{M}_{orh} \mathbf{M}_{vp} = \begin{bmatrix}
\frac{n_x}{r – l} & 0 & 0 & -\frac{l n_x}{r – l} – \frac{1}{2} \\
0 & \frac{n_y}{t – b} & 0 & -\frac{b n_y}{t – b} – \frac{1}{2}\\
0 & 0 & \frac{2}{n – f} & -\frac{n + f}{n – f} \\
0 & 0 & 0 & 1
\end{bmatrix}.$$不妨记$$x_h = r, x_l = l, \\ x_h’ = n_x – \frac{1}{2}, x_l’ = -\frac{1}{2}, \\ y_h = t, y_l = b, \\ y_h’ = n_y – \frac{1}{2}, y_l’ = -\frac{1}{2}, \\ z_h = n, z_l = g, \\ z_h’ = 1, z_l’ = -1,$$则上述正交投影矩阵$\mathbf{M}_{orh}$与视口变换矩阵$\mathbf{M}_{vp}$相乘的结果可简记为$$\begin{bmatrix}
\frac{x_h’ – x_l’}{x_h – x_l} & 0 & 0 & \frac{x_l’ x_h – x_h’ x_l}{x_h – x_l} \\
0 & \frac{y_h’ – y_l’}{y_h – y_l} & 0 & \frac{y_l’ y_h – y_h’ y_l}{y_h – y_l} \\
0 & 0 & \frac{z_h’ – z_l’}{z_h – z_l} & \frac{z_l’ z_h – z_h’ z_l}{z_h – z_l} \\
0 & 0 & 0 & 1
\end{bmatrix}.$$
7.3 证明经正交投影变换后, 近平面上的点依旧在近平面上, 远平面上的点依旧在远平面上.
$\\$ 证: 将一个正交投影矩阵作用于近平面上的点的齐次坐标上, 我们可得$$\mathbf{M}_{orh} \mathbf{x} = \begin{bmatrix}
\frac{2}{r – l} & 0 & 0 & -\frac{r + l}{r – l} \\
0 & \frac{2}{t – b} & 0 & -\frac{t + b}{t – b} \\
0 & 0 & \frac{2}{n – f} & -\frac{n + f}{n – f} \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x \\
y \\
n \\
1
\end{bmatrix} = \begin{bmatrix}
\frac{2}{r – l} x – \frac{r + l}{r – l}\\
\frac{2}{t – b} y – \frac{t + b}{t – b} \\
1 \\
1
\end{bmatrix}.$$故经正交投影变换后, 近平面上的点依旧在近平面上. 同理可得, 经正交投影变换后, 远平面上的点依旧在远平面上. 命题得证.
7.4 使用代数方法证明透视矩阵能够保持待变换点在View Volume内的坐标的$z$分量顺序.
$\\$ 证: 投影变换是整个渲染管线里, 设计得最复杂的, 也最巧妙的一次变换. 其实基本理解了这些变换, 对整个渲染管线就有了大概的认识了. 接下来我们一步步来讨论, 为什么投影变换矩阵要这么设计? 为什么裁剪在透视除法之前? 为什么观察坐标系是右手坐标系? 如何实现的近大远小? 如何实现的Early-Z?
7.4.1 投影变换的目的
坐标转换到观察空间后, 由于直接使用摄像机的平截头体进行裁剪比较复杂(平截头体的边界方程求交困难), 所以需要将其转化到裁剪空间(Clip空间).
$\\$ 从观察空间到裁剪空间的变换叫做投影变换.
$\\$ 裁剪空间变换的思路是, 对平截头体进行缩放, 使近裁剪面和远裁剪面变成正方形, 使坐标的$w$分量表示裁剪范围, 此时, 只需要简单的比较$x$, $y$, $z$和$w$分量的大小即可裁剪图元.
$\\$ 虽然叫做投影变换, 但是投影变换并没有进行真正的投影.
7.4.2 透视投影变换分2步:
$\cdot$ 从Frustum内一点投影到近剪裁平面.
$\\$ $\cdot$ 由近剪裁平面缩放成规则观察体(Canonical View Volume), CVV空间, 得到Clip坐标(此时没有除以$w$变成3D坐标, 是齐次坐标).
$\\$ 相机空间中的顶点, 如果在视锥体中, 则变换后就在CVV中. 如果在视锥体外, 变换后就在CVV外. CVV本身的规则性对于多边形的裁剪很有利.
7.4.3 透视投影推导
投影坐标系有两种矩阵: 透视矩阵和正交矩阵, 我们选择OpenGL的透视投影变换进行分析:
$\\$ 1) 第一步: 投影到近剪裁平面
$\\$ 我们先从一个方向考察投影关系. 设$\mathbf{P}(x, z)$是经过相机变换之后的点, 视锥体由眼睛位置Eye, 近裁剪平面$np$与远裁剪平面$fp$组成. 此外, $N$是眼睛到近裁剪平面的距离, $F$是眼睛到远裁剪平面的距离, 选择近裁剪平面作为投影平面. 设$\mathbf{P”}(x”, z”)$是投影之后的点, 则有$z’ = -N$. 通过相似三角形性质:$$x / x’ = z / z’ = z / -N,$$所以$$x’ = -N * x / z.$$同理, 有$$y’ = -N * y / z.$$这样, 我们便得到了$\mathbf{P}$投影后的点$\mathbf{P’}$,$$\mathbf{P’} = (-N * x / z, -N * y / z, -N).$$从上面可以看出, 当Frustum内的点投影到近剪裁平面的时候, 投影的结果$z”$始终等于$-N$, 在投影面上. 实际上, $z”$对于投影后的$\mathbf{P”}$已经没有意义了. 此处, 点$\mathbf{P”}$由$\mathbf{P}$投影后的点$\mathbf{P’}$忽略$y$分量后得到.
$\\$ 2) 充分利用$z’$值, 一步步对$z’$改造
$\\$ $\cdot$ 后面在进入片元操作之前还有Early-Z测试, 有必要把投影之前的$z$保存下来, 方便后面使用.
$\\$ 所有位于线段$\mathbf{P’} \mathbf{P}$上的点, 最终都会投影到$\mathbf{P’}$点, 那么如果这条线段上有多个点, 如何确定最终保留哪一个呢? 当然是离观察这最近的这个了, 也就是深度值($z$值) 最小的. 所以$z’$坐标需要保存$\mathbf{P’}$点的$z$值. 那么$$\mathbf{P’} = (-N * x / z, -N * y / z, z).$$又因为在光栅化之前, 我们需要对$z$坐标进行插值.
$\\$ $\cdot$ 后面投影之后的光栅化阶段, 要通过$x’$和$y’$对$z$进行线性插值, 以求出三角形内部片元的$z$, 进行Z缓冲深度测试.
$\\$ 从$x’ = -N * x / z$可以看出, 投影后的$x’$和$y’$, 与$z$不是线性关系, 与$1 / z$才是线性关系. 所以用$1 / z$的线性组合值和$x’$, $y’$一起插值才是正确的.
$\\$ $\cdot$ 同时为了保证近处精度更高, 我们使用$z$坐标的的倒数$$z’ = 1 / z.$$$\cdot$ $\mathbf{P’}$的3个代数分量统一地除以分母$-z$, 易于使用齐次坐标变为普通坐标来完成.
$\\$ 所以: 我们暂时得到的新的点$\mathbf{P’}$表示为:$$\mathbf{P’} = (-N * x / z, -N * y / z, -1 / z).$$3) 第2步: 缩放到CVV空间
$\\$ CVV是一个$x$, $y$, $z$的范围都为[-1, 1]的规则体, 便于进行多边形裁剪.
$\\$ 我们先不管$x$和$y$, 先映射$z$到[-1, 1]之间. 要进行映射,常用的主要是Wrap和线性映射, 我们直接使用线性公式:
$\\$ 我们对$-1 / z$适当的选择系数$a$和$b$, 也就是$$a + b * (-1 / z),$$这个式子在$z = -N$的时候值为-1, 而在$z = -F$的时候值为1, 从而在$z$方向上构建CVV.
$\\$所以最终记录的$\mathbf{P}$的$z$值:$$z’ = -(a + b/ z),$$所以: 我们得到的新的点暂时表示为:$$\mathbf{P’} = (-N \frac{x}{z}, -N \frac{y}{z}, -\frac{az + b}{z}).$$我们为了在GPU中运算更快, 同时能合并之前的矩阵变换, 所以我们最终要使用矩阵形式来做透视变换. 所以这一步还是要转为齐次坐标$$\mathbf{P’} = (-N * x / z, -N * y / z, -(a + b / z), 1).$$对于齐次坐标, 我们可以对所有项乘以一个相同的值, 不会改变他的位置.$$\mathbf{P’} = \mathbf{P’} * (-z) = (N * x, N * y, (az + b), -z).$$所以我们可以凑出下面的矩阵乘法:$$\begin{pmatrix}
N & 0 & 0 & 0 \\
0 & N & 0 & 0 \\
0 & 0 & a & b \\
0 & 0 & -1 & 0
\end{pmatrix} \begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix} = \begin{pmatrix}
Nx \\
Ny \\
az + b \\
-z
\end{pmatrix} \sim \begin{pmatrix}
-Nx / z \\
-Ny / z \\
-(az + b) / z \\
1
\end{pmatrix},$$这一步在透视投影过程中称为透视除法(Perspective Division), 这是透视投影变换的第2步, 经过这一步, 就丢弃了原始的$z$值(得到了CVV中对应的$z$值), 顶点才算完成了投影. 而在这两步之间的就是CVV裁剪过程, 所以裁剪空间使用的是齐次坐标.
$\\$ 为什么不把透视除法整合到矩阵中? 我们在后面详细讨论原因.
$\\$ 接下来我们就求出$a$和$b$: 因为CVV是-1到1范围, 所以:$$-\frac{az + b}{z} = \left\{\begin{matrix}
-1, & when \ z = -N, \\
1, & when \ z = -F.
\end{matrix}\right.$$所以:$$a = -\frac{F + N}{F – N}, \\ b = \frac{-2FN}{F – N}.$$我们得到了透视投影矩阵的第一个版本:$$\begin{pmatrix}
N & 0 & 0 & 0 \\
0 & N & 0 & 0 \\
0 & 0 & a & b \\
0 & 0 & -1 & 0
\end{pmatrix},$$其中, $a = -\frac{F + N}{F – N}$, $b = \frac{-2FN}{F – N}.$