最近在学习TopoXu老师的拓扑数据分析课程, 许多课程内容参考了蒋伯驹老师的《绳圈的数学》一书. 但遗憾的是, 书上对于亚历山大多项式及康威方法介绍的篇幅很少, 而这一部分却又是纽结理论里极其重要的一部分, 因此特以本文记录一些关于亚历山大多项式及康威方法的要点.
参考材料
1. 拓扑数据分析lecture4_part1
2. 拓扑数据分析lecture4_part2
3. 纽结理论和琼斯多项式
4. 姜伯驹. 绳圈的数学[M]. 湖南敎育出版社, 1991.
历史上第一个纽结的拓扑不变量是亚历山大多项式Alexander Polynomial, 它是由James Alexander于1928年剔除. 它可以用于区分一部分纽结. 只要两个纽结$L$和$L’$的亚历山大多项式不相同, 则它们一定是彼此不同痕的. 但如果两个纽结的亚历山大多项式计算结果相同的话, 我们却并不能说它们就是彼此同痕的纽结. 我们将在本文的末尾, 给出一个不平凡的例子, 它的亚历山大多项式与平凡纽结的相同, 但它一定不是平凡纽结.
1. 亚历山大多项式的定义
纽结的亚历山大多项式其本质是单变量洛朗多项式Laurant Polynominal. 洛朗多项式与普通多项式的不同点在于它允许变量的负整数次幂的出现. 即$L(t) = t + 1 + t^{-1}$是洛朗多项式的一个例子. 事实上, 亚历山大多项式与琼斯多项式的本质都是单变量洛朗多项式, 而HOMFLY多项式则是双变量洛朗多项式.
亚历山大多项式的计算方式有两种, 第一种是由James Alexander本人在原始论文提出的, 用的方法是计算投影图索决定的矩阵的行列式. 第二种是由John H.Conway于1969年提出, 他使用一种被称作是Skein Relation的方式, 这种方式推广性很强, 可以用于琼斯多项式及其HOMFLY多项式的计算.
为了后面的表述方便, 我们把第一种方法称为亚历山大方法, 第二种方法称为康威方法. 亚历山大多项式有的时候也被称作是亚历山大-康威多项式Alexander-Conway Polynominal.
2. 康威方法
康威方法的计算法则主要遵循以下两条方程:
$\\$ Rule 1. $\bigtriangleup (\bigcirc) = 1$.
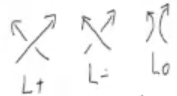
Rule 2. $\bigtriangleup(L_+) – \bigtriangleup(L_-) + (t^{\frac{1}{2}} – t^{-\frac{1}{2}})\bigtriangleup(L_0) = 0$.
$\\$ $\cdot$ 法则一: 在方程中, 所有出现的平凡纽结及其等价投影图的亚历山大多项式都是1.
$\\$ $\cdot$ 法则二: 拆接关系式Skein Relation, 主要针对纽结的其中一个交叉点, 此时纽结可能是$L_+$或者$L_-$之一(有的时候也可能是$L_0$), 然后写出该交叉点的另外一种投影图, 以及去除该交叉点的投影图, 并乘以相关的系数(可能包含未知数$t$) 用以组成方程. 即$$\bigtriangleup(L_+) – \bigtriangleup(L_-) + (t^{\frac{1}{2}} – t^{-\frac{1}{2}})\bigtriangleup(L_0) = 0.$$康威方法就是反复利用以上两个法则, 逐个解开交叉点, 并且利用R-Moves和已知纽结或链环的计算结果, 迭代得出目标纽结或链环的计算结果. 注意: 此处我们利用了一个事实, 就是亚历山大多项式在R-Moves下保持不变, 其证明可以参看亚历山大的原文.