最近在复习Mesh减面相关的知识点, 当初读罢Hoppe H. New quadric metric for simplifying meshes with appearance attributes[C]//Proceedings Visualization’99 (Cat. No. 99CB37067). IEEE, 1999: 59-510.这篇论文后开发了Mesh自动减面模块, 但其实并没有完全吃透这篇论文, 对许多理论细节亦是囫囵吞枣. 时隔近两年, 重新阅读这篇论文, “柳暗花明又一村”, 对于之前许多令自己迷惑的理论细节豁然开朗~
参考材料
1. Hoppe H. New quadric metric for simplifying meshes with appearance attributes[C]//Proceedings Visualization’99 (Cat. No. 99CB37067). IEEE, 1999: 59-510.
2. 点云法向量和平面方程
1. 传统的关于几何的二次误差度量
传统的关于几何的二次误差度量在原始Mesh的每个面$f$上定义了一个二次误差度量$Q^f(\mathbf{v})$, 该二次误差度量值等于点$\mathbf{v} = (\mathbf{p}) \in \mathbb{R}^3$到包含面$f$的平面的距离的平方. 原始Mesh的每个顶点$v$上定义的二次误差度量值等于顶点$v$的相邻面的按面积加权的二次误差度量值之和:\begin{equation}Q^v(\mathbf{v}) = \sum_{f \ni v} area(f) \cdot Q^f(\mathbf{v}).\label{quadratic_error_functions_defined_on_vertices}\end{equation}每次边塌缩$(v_1, v_2) \to v$后, 新顶点$v$的位置将被更新为$\mathbf{v}$ s.t. $Q^v(\mathbf{v}) = $$ Q^{v_1}( $$ \mathbf{v}) + Q^{v_2}(\mathbf{v})$极小化, 且下一条塌缩的边将具有最低的$Q^v(\mathbf{v})$极小值.
$\\$ 接下来推导给定面$f = (v_1, v_2, v_3)$上的$Q^f(\mathbf{v})$. 令$\mathbf{v} = (\mathbf{p})$, 则$\mathbf{p}$到包含$f$的平面$P \subset \mathbb{R}^3$的有向距离为$\mathbf{n}^T \mathbf{p} + d$, 其中,$$\mathbf{n} = (\mathbf{p}_2 – \mathbf{p}_1) \times (\mathbf{p}_3 – \mathbf{p}_1) / \left \| \mathbf{n} = (\mathbf{p}_2 – \mathbf{p}_1) \times (\mathbf{p}_3 – \mathbf{p}_1) \right \| $$为面法线, 标量$d = -\mathbf{n}^T \mathbf{p}_1$. 此外, 另外一种计算上述参数的方式是求解下述线性方程组$$\begin{pmatrix}
\mathbf{p}_1^T & 1 \\
\mathbf{p}_2^T & 1 \\
\mathbf{p}_3^T & 1 \\
\end{pmatrix} \begin{pmatrix}
\mathbf{n} \\
\\
d
\end{pmatrix} = \begin{pmatrix}
0 \\
0 \\
0
\end{pmatrix},$$附加的约束条件为$\left \| \mathbf{n} \right \| = 1$.
$\\$ 故点$\mathbf{p}$到平面$P$的距离的平方为$$Q^f(\mathbf{v} = (\mathbf{p})) = (\mathbf{n}^T\mathbf{v} + d)^2 = \mathbf{v}^T (\mathbf{n} \mathbf{n}^T) \mathbf{v} + 2d\mathbf{n}^T \mathbf{v} + d^2,$$其可以表示为一个二次函数$\mathbf{v}^T \mathbf{A} \mathbf{v} + 2\mathbf{b}^T \mathbf{v} + c$, 其中, $\mathbf{A}$为$3 \times 3$对称矩阵, $\mathbf{b}$为3维列向量, $c$为标量. 从而,$$Q^f = (\mathbf{A}, \mathbf{b}, c) = (\mathbf{n} \mathbf{n}^T, d\mathbf{n}, d^2)$$可用6 + 3 + 1 = 10个系数进行存储. 这种表示的优点是, 式$\ref{quadratic_error_functions_defined_on_vertices}$中的二次误差度量$Q^v$是通过上述系数向量的简单线性组合得到的.
$\\$ 在一次边塌缩后, 可得新的顶点位置$\mathbf{v}_{min}$ s.t. $Q^v(\mathbf{v})$极小化, 即梯度$$\bigtriangledown Q^v(\mathbf{v}) = 2 \mathbf{A} \mathbf{v} + 2\mathbf{b} = 0,$$计算新的顶点位置$\mathbf{v}_{min}$的方式是求解下述线性方程组\begin{equation}\mathbf{A} \mathbf{v}_{min} = -\mathbf{b}.\label{found_vertex_position}\end{equation}
2. 传统的关于几何与其它顶点属性的二次误差度量
Garland与Heckbert扩展了他们的框架用于计算包含其它顶点属性的二次误差度量. 他们的方法是将$\mathbb{R}^3$中点到平面的距离度量推广至$\mathbb{R}^{3 + m}$中的点到超平面的距离度量, 其中, $m$为其它顶点属性的维度和. 即, 对于$\mathbf{v} = \begin{pmatrix}
\mathbf{p} \\
\mathbf{s}
\end{pmatrix} \in \mathbb{R}^{3 + m}$, $Q^f(\mathbf{v})$被定义为$\mathbb{R}^{3 + m}$中从$\mathbf{v}$到由三个顶点$(\mathbf{v}_1, $$ \mathbf{v}_2, \mathbf{v}_3)$张成的仿射子空间$P’ $$ \subset \mathbb{R}^{3 + m}$的距离.
$\\$ 令$\mathbf{v}’$表示$\mathbf{v}$在该仿射子空间上的投影. 误差$Q^f(\mathbf{v}) = \left \| \mathbf{v} – \mathbf{v}’ \right \|^2$可以看作是几何距离误差$\left \| \mathbf{p} – \mathbf{p}’ \right \|^2$与属性距离误差$\left \| \mathbf{s} – \mathbf{s}’ \right \|^2$这两项的总和. 注意到点$\mathbf{p}’$并非如前所述为点$\mathbf{p}$在平面$P \subset \mathbb{R}^3$上的投影. Garland与Heckbert并非将$\mathbf{v}$与$\mathbb{R}^3$中欧式距离最近的点进行比较, 而是与属性值更接近的点进行对比. 然而, 该对比策略可能低估了$\mathbf{v}$与$\mathbf{v}’$在$\mathbb{R}^3$中的欧氏距离.
$\\$ 二次误差度量$Q^f(\mathbf{v})$由一个$(3 + m) \times (3 + m)$矩阵$\mathbf{A}$, 一个$3 + m$维列向量$\mathbf{b}$与一个标量$c$组成. 由于由上述公式得到的矩阵$\mathbf{A}$是稠密的实对称矩阵, 故$Q$的存储需要共计$$(1 + (3 + m))(3 + m) / 2 + (3 + m) + 1 = (4 + m)(5 + m) / 2$$个系数, 即系数数量是一个关于$m$的二次函数.
$\\$ 为了权衡几何精度和属性精度, 用户为每个属性$j \in \{ 1 \dots m \}$指定相对重要性权重$\lambda_j$, 该相对重要性权重$\lambda_j$预先乘以属性值, 对$\mathbb{R}^{3 + m}$中的部分轴进行了有效的缩放. 为了规避Mesh大小对于算法的影响, 应对Mesh进行归一化, 使其外接球为单位球.
3. 本文提出的二次误差度量
本文的贡献是引入了一种新的二次误差度量, 该度量基于3D空间中的几何对应关系定义了几何误差与属性误差. 本文不是将给定点投影到抽象的高维空间$\mathbb{R}^{3 + m}$中的Mesh面上, 而是在$\mathbb{R}^3$中进行投影, 并根据这种对应关系计算几何误差与属性误差.
$\\$ 面$f$的二次误差度量定义为$$Q^f(\mathbf{v} = \begin{pmatrix}
\mathbf{p} \\
\mathbf{s}
\end{pmatrix}) = Q^f_p(\mathbf{v}) + \sum^m_{j = 1} Q^f_{s_j}(\mathbf{v}),$$其中, 几何误差$Q^f_p(\mathbf{v})$为从$\mathbf{p}$到在包含$f$的平面$P \subset \mathbb{R}^3$上的投影点$\mathbf{p}’$的距离的平方, 属性误差$Q^f_{s_j}(\mathbf{v})$为在投影点$\mathbf{p}’$处根据面$f$的顶点属性值插值的属性值$\mathbf{s}’$与$\mathbf{s}$的距离的平方. 接下来推导这些项的计算过程.
$\\$ 本文所使用的几何误差项仅是通过将传统的几何误差项进行简单扩展得到的:
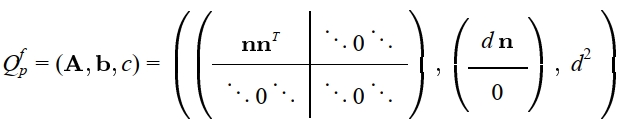
其中, $\mathbf{A}$与$\mathbf{b}$中的分隔线标记了前3行与前3列.
$\\$ 为了计算属性误差项$Q^f_{s_j}$, 本文首先定义一个线性泛函$$\widehat{s}_j(\mathbf{p}) = \mathbf{g}^T_j \mathbf{p} + d_j$$用于表示于点$\mathbf{p} \in \mathbb{R}^{3}$处的期望属性值. 梯度$\mathbf{g}_j$与标量$d_j$定义如下所示. 自然地, $\widehat{s}_j(\mathbf{p})$应该由面顶点$f = (\begin{pmatrix}
\mathbf{p}_1 \\
\mathbf{s}_1
\end{pmatrix}, \begin{pmatrix}
\mathbf{p}_2 \\
\mathbf{s}_2
\end{pmatrix}, \begin{pmatrix}
\mathbf{p}_3 \\
\mathbf{s}_3
\end{pmatrix})$插值得到, 从而匹配平面$P$上的线性插值结果. 此外, 对于任意$\mathbf{p} \in \mathbb{R}^3$, $\widehat{s}_j(\mathbf{p})$应与$\mathbf{p}$在$P$上的几何投影处的属性值$\widehat{s}_j(\mathbf{p}’)$相同; 这等价于令$\mathbf{n}^T \mathbf{g}_j = $$ 0$. 故$\mathbf{g}_j$为标量函数在三角面上的梯度. 可通过求解下述$4 \times 4$的线性方程组计算参数$(\mathbf{g}_j, d_j)$$$\begin{pmatrix}
\mathbf{p}^T_1 & 1 \\
\mathbf{p}^T_2 & 1 \\
\mathbf{p}^T_3 & 1 \\
\mathbf{n}^T & 1
\end{pmatrix} \begin{pmatrix}
\mathbf{g}_j \\
d_j
\end{pmatrix} = \begin{pmatrix}
s_{1, j} \\
s_{2, j} \\
s_{3, j} \\
0
\end{pmatrix}.$$因为$Q^f_{s_j}(\mathbf{v}) = (\widehat{s}_j(\mathbf{p}) – s_j)^2 = (\mathbf{g}^T_j \mathbf{p} + d_j – s_j)^2$, 通过代数重排可得$Q^f_{s_j} = $$ (\mathbf{A}, \mathbf{b}, c) = $
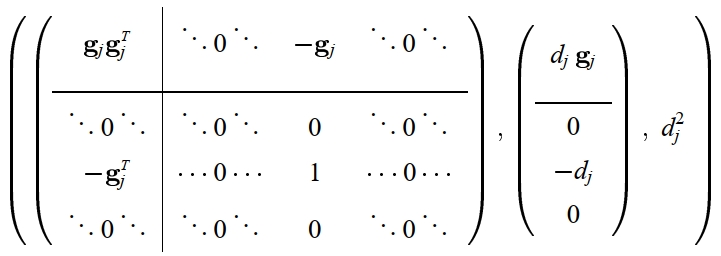
其中, 值1出现于$\mathbf{A}_{3 + j, 3 + j}$中, $-d_j$出现于$\mathbf{b}_{3 + j}$中. 不难验证, $$Q^f_{s_j} = \begin{bmatrix}
\begin{array}{c | c}
\mathbf{p}^T & \cdots s_j \cdots
\end{array}
\end{bmatrix} \mathbf{A} \begin{bmatrix}
\begin{array}{c}
\mathbf{p} \\ \hline
\vdots \\
s_j \\
\vdots
\end{array}
\end{bmatrix} + \mathbf{b}^T \begin{bmatrix}
\begin{array}{c}
\mathbf{p} \\ \hline
\vdots \\
s_j \\
\vdots
\end{array}
\end{bmatrix} + c.$$将所有关于$s_j$的二次误差度量累加可得$Q^f = (\mathbf{A}, \mathbf{b}, c) = $
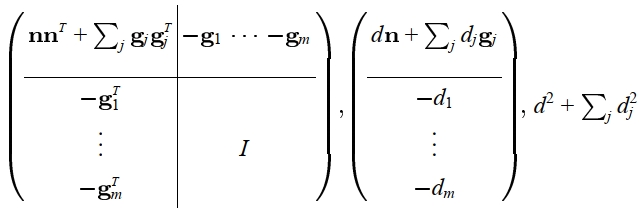
注意到, $\mathbf{A}$的前3行与前3列是稠密的, 剩余的$m \times m$子矩阵为单位矩阵$I$. 回顾一下, 一组权重$\lambda_j$用于缩放属性误差相对于几何误差的大小. 若定义$Q = Q_p + $$ \sum_j \lambda_j^2 Q_{s_j}$, 则子矩阵对角线上的元素对应的权重为$\lambda_j^2$. 本文使用更简单的方法, 在构造和计算$Q$之前, 通过$\lambda_j$对属性值$s_j$进行预缩放. 在任何情况下, $m \times m$子矩阵总为一个单位矩阵与一个标量因子的乘积, 因此仅需存储一个系数. 总体而言, 存储$Q$需要存储$11 + 4m$个系数, 这关于$m$是线性的, 如下表所示.
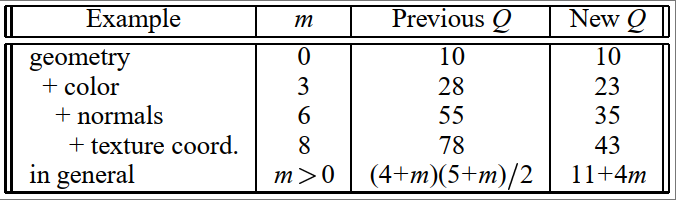
$\\$ 某些属性值(如颜色通道) 是有界的(如$0 \le r, g, b \le 1$). 式$\ref{found_vertex_position}$中的$\mathbf{v}_{min}$可能包含这些线性不等式约束之外的属性值分量. 当这种情况发生时, 一种回退策略可能是解决计算代价更昂贵的带约束的二次规划问题. 然而, 本文选择简单地将属性值截断到其边界, 并重新计算$Q^v(\mathbf{v})$. 同理, 曲面上的法线属性向量应保持模长为1的特征. 然而, 二次约束二次规划问题是一个更困难的问题, 因此本文选择不对法线属性分量进行截断等操作, 并重新对法线属性向量进行归一化.
4. 属性的不连续性
Mesh的属性通常是不连续的. 例如, 折痕是Mesh上法线不连续的边缘链. 在辐射度量学中, 如果相邻Patches不平行, 则Patches上的强度通常不同. 对这种不连续性进行建模需要为每个顶点存储多组属性值. 为此, 本文选择在所使用的数据结构中引入楔的概念, 如下图所示.
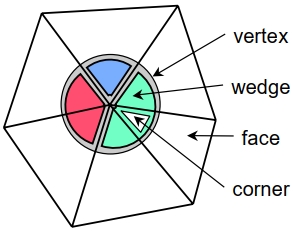
一个顶点被划分为$k \ge 1$个楔, 每个楔$w_i$都有自己的属性向量$\mathbf{s}^i$. 与顶点相邻的每个面的角被指定给其中一个楔. 楔$w_i$处的二次误差度量$Q^{w_i}(\mathbf{p}, $$ \mathbf{s}^i)$为其相邻面对应的$Q^f$的面积加权和,\begin{equation}Q^w(\mathbf{v}) = \sum_{f \ni w} area(f) \cdot Q^f(\mathbf{v}),\label{quadratic_error_functions_defined_on_wedges}\end{equation}则式$\ref{quadratic_error_functions_defined_on_vertices}$被替换为\begin{equation}Q^v(\mathbf{p}, \mathbf{s}^1, \dots, \mathbf{s}^k) = \sum^k_{i = 1} Q^{w_i}(\mathbf{p}, \mathbf{s}^i).\label{replaced_quadratic_error_functions_defined_on_vertices}\end{equation}新顶点的二次误差度量$Q^v$的维数为$3 + km$. 注意到, 该维数可变的二次误差度量$Q^v$不需要显式存储在Mesh上, 因为当考虑边塌缩时, 可以简单地从$Q^{w_i}$构造得到$Q^v$. 最小化该二次误差度量$Q^v$可同时得到新的顶点位置及其所有楔的属性.
$\\$ 对于边塌缩, 必须重新定义楔合并后其二次误差度量的合并策略(类似于$Q^v(\mathbf{v}) $$ = Q^{v_1}(\mathbf{v}) + Q^{v_2}(\mathbf{v})$). 参见下图, 若$w_a$与$w_b$在边坍塌前均与面$f_1$相邻, 则在边坍塌后$w_a$与$w_b$相邻, 并重新记为$w_a’$与$w_b’$, 同样地, 在面$f_2$的另一侧亦是如此.
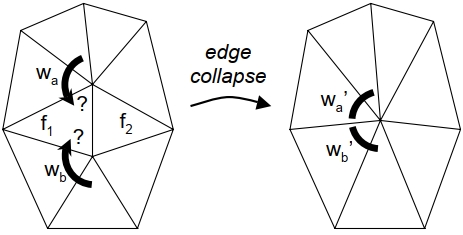
对于每对被边塌缩影响的楔(0对, 1对或2对), 本文将它们的楔的二次误差度量进行求和. 当顶点$v_1$与$v_2$均仅有一个楔时, 通过这些规则得到的塌缩效果与原始方案一致.
$\\$ 最后一个细节是, 本文通过为每条尖锐边(包括边界边) 添加额外的二次误差度量来保持不连续曲线的几何形状. 在本文的框架中, 该边的二次误差度量被添加到与边相邻的4个角上的$Q^w(\mathbf{v})$上(或者在边界边的情况下为2个角).
5. 减面优化
除了定义新的QEM, 本文还尝试了两种技术, 占用内存更少的减面算法与保持体积的算法, 发现它们进一步改善了结果.
5.1 占用内存更少的减面算法
本文没有将$Q^w(\mathbf{v})$分配给原始Mesh中的楔, 并通过$Q^v(\mathbf{v}) = Q^{v_1}(\mathbf{v}) + Q^{v_2}( $$ \mathbf{v})$在每次边塌缩后对$Q^w(\mathbf{v})$进行累加, 而是尝试了另一种占用内存更少的减面算法, 算法执行过程中根据已简化的Mesh的几何形状与属性不断重新计算$Q^w( $$ \mathbf{v})$. 因此, 在执行边塌缩$(v_1, $$ v_2) \to v$时, 我们使用式$\ref{quadratic_error_functions_defined_on_wedges}$与式$\ref{replaced_quadratic_error_functions_defined_on_vertices}$在下图所示的面集合$F^{i + 1}$上计算$Q^v( $$ \mathbf{v})$.
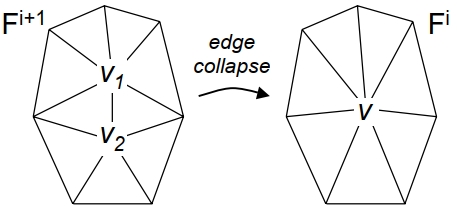
本文证实了占用内存更少的减面算法提高了结果的准确性. 虽然这起初可能看起来违反直觉, 但可以通过下图来解释.
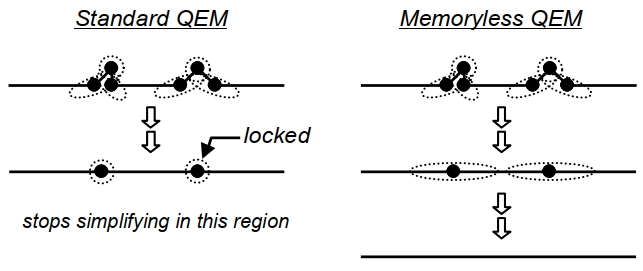
标准QEM算法在原始Mesh上计算$Q^v$, 然后求和. 结果, 非平行椭圆(对应于精细特征) 的合并产生紧密的形状为球面的二次误差度量, 锁定顶点并防止进一步简化, 即使顶点均处于同一平面上. 接下来分步解释上图.
$\cdot$ 椭圆几何约束的本质
$\\$ 在QEM框架中, 每个椭圆代表顶点在保持局部形状精度下的可移动范围(即不显著增加二次误差的区域). 椭圆的:
$\\$ a) 方向: 由矩阵$Q^f$的最小特征值对应的特征向量决定(法向量方向, 详见参考材料2).
$\\$ b) 形状: 由特征值的比值决定(各向异性程度).
$\\$ c) 范围: 由特征值的倒数平方根决定(沿各轴的移动自由度).
$\cdot$ 非平行椭圆的约束冲突
$\\$ 当两个椭圆非平行时:
$\\$ a) 方向差异: 它们的法向量方向不一致.
$\\$ b) 约束互补性: 每个椭圆在不同方向上施加约束. 例如:
$\\$ $\quad$ – 椭圆A可能在$x-y$平面方向约束强.
$\\$ $\quad$ – 椭圆B可能在$y-z$平面方向约束强.
$\\$ c) 交集区域: 这种方向差异导致它们的交集区域必须同时满足两个方向的约束, 相当于在三维空间中被”双向挤压”.
$\cdot$ 矩阵合并的代数效应
$\\$ 合并两个顶点的$Q^f$矩阵时:
$\\$ a) 矩阵相加: 新矩阵$Q_{new} = Q_1 + Q_2$.
$\\$ b) 特征值增强: 由于$Q_1$与$Q_2$在不同方向上存在约束, 相加后:
$\\$ $\quad$ – 在共有约束方向(如法向量方向) 的特征值会显著增大.
$\\$ $\quad$ – 在其他方向的特征值也会因矩阵非对角元素耦合而增大.
$\\$ c) 球形化趋势: 当各方向特征值趋于接近时, 椭圆方程退化为球面方程. 合并后的矩阵特征值分布更均匀, 导致约束区域接近球形.
$\cdot$ 自由度锁定机制
$\\$ a) 移动范围收缩: 原始椭圆允许顶点在特定平面内移动(如沿椭圆长轴), 但合并后的球形约束要求顶点在所有方向上保持接近原始位置.
$\\$ b) 误差敏感区扩大: 任何偏离原始位置的运动都会显著影响所有方向的误差度量, 形成”锁定效应”.
$\\$ c) 简化停滞: 即使整体形状已接近平面, 顶点仍被限制在原始位置附近, 无法进一步合并或移动.
相比之下, 在使用占用内存更少的减面算法的情况下, $Q^v$是在算法执行过程中根据已简化的Mesh的几何形状与属性不断重新计算的. 这种忘记更精细的细节的能力允许在需要时进一步简化.
$\\$ 尽管占用内存更少的减面算法降低了存储QEM这一步骤的必要性, 但为了加快算法速度, 本文发现在Mesh的面上缓存值($area(f) \cdot Q^f(\mathbf{v})$) 是有用的, 并在边塌缩时适当地更新它们. 因此, 本文提出的新QEM的紧凑形式仍然具有优势.
5.2 保持体积
实验表明, 新的QEM有时会在属性高梯度区域缩小Mesh的几何形状. 也就是说, 在尖锐的属性值过渡处, 新顶点$\mathbf{v}$可能被推向曲面上旧顶点的曲率中心.
$\\$ 下图以$\mathbb{R}^2$中多边形曲线的简化为例直观地说明了这个现象. 在原始Mesh上定义的标量场从$\mathbf{1}$变化至$\mathbf{0}$. 显然, 在这个邻域上的边塌缩无法保留这个属性字段. 接下来考虑二次度量所测量的误差.
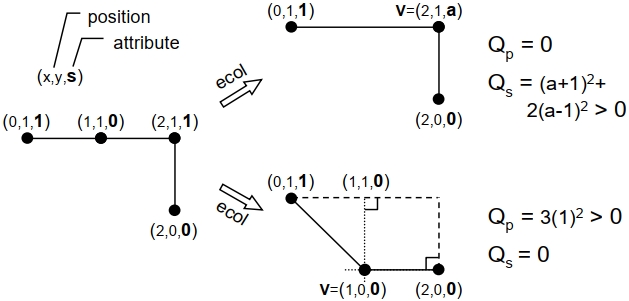
在上图右上角中, 边塌缩后几何体体积将完全保持($Q_p = 0$), 但属性误差$Q_s$不为0. 原因是顶点$\mathbf{v} =(2, 1, \mathbf{a})$的属性值$\mathbf{a}$不能同时在所有3个原始线段上插值属性梯度. 特别地, 必须将$\mathbf{a}$设置为$\mathbf{-1}$来外插最左侧的段线段$[(0, 1, \mathbf{1}), (1, 1, \mathbf{0})]$.
$\\$ 另一方面, 在上图右下角中, 边塌缩会导致几何误差$Q_p > 0$, 但”实现” 了$Q_s = $$ 0$, 因为$\mathbf{v} =(1, 0, \mathbf{0})$在原始3条线段上的每一个投影点均精确地插值了原始属性. 直观上, 顶点朝向其曲率中心的运动允许它投影到原始线段的内部, 从而避免属性外插.
$\\$ 为了抵消几何收缩的影响, 本文引入了保持体积的约束. 在边塌缩过程中保持体积等价于下述在合并后的顶点$\mathbf{v}$的位置$\mathbf{p}$上的线性约束$$\mathbf{g}^T_{VOL} \mathbf{p} + d_{VOL} = 0.$$其中, 体积梯度$\mathbf{g}^T_{VOL}$为$F^{i + 1}$的面法线的加权和, 每一条面法线的权重为对应面的面积的三分之一. 本文利用上式来约束Mesh体积, 主要是因为上式定义了一个平面方程, 通过调整平面的法向量和与原点的距离, 可以控制Mesh的体积变化. 在Mesh简化过程中, 将这个平面方程作为优化目标的一部分, 有助于保持简化后Mesh的体积与原始Mesh尽可能接近. 这种方法不仅提高了Mesh简化的质量, 还保持了Mesh的视觉效果与几何准确性. 使用拉格朗日乘数法(其对应的拉格朗日乘数为$\lambda$) 可以很容易地计算受线性约束的$Q^v(\mathbf{v})$的极小值:$$\begin{pmatrix}
\mathbf{A} & \mathbf{g}_{VOL} \\
\mathbf{g}^T_{VOL} & 0
\end{pmatrix} \begin{pmatrix}
\mathbf{v}_{min} \\
\lambda
\end{pmatrix} = \begin{pmatrix}
-\mathbf{b} \\
-d_{VOL}
\end{pmatrix}.$$若顶点$\mathbf{v}$在Mesh上的邻域的高斯曲率为0, 即若它的形状为平面或圆柱形, 则该线性方程组的系数矩阵(即式$\ref{found_vertex_position}$中的系数矩阵) 可能是病态的.
$\\$ 证: 先证, 对于任意$n$维非零向量$\mathbf{a}$, $\mathbf{b}$, $\mathbf{a} \mathbf{b}^T$为一个$n \times n$的秩1矩阵.
$\\$ 不妨令$\mathbf{b} = (b_1, \cdots, b_n)^T$, 则$$\mathbf{a} \mathbf{b}^T = (\mathbf{a} b_1, \cdots, \mathbf{a} b_n),$$每一列向量构成的向量组是线性相关的(每一列向量均为$\mathbf{a}$的倍数), 故$\mathbf{a} \mathbf{b}^T$为一个$n \times n$的秩1矩阵.
$\\$ 由于顶点$\mathbf{v}$在Mesh上的邻域为平面或圆柱形, 即$\mathbf{v}$的相邻面的法向$\mathbf{n}_i, i $$ \in \{1, 2 $$ , \cdots, k\}$几乎一致, 其中, $k$为$\mathbf{v}$的相邻面数量, 不妨令其相邻面的法向均为$\mathbf{n}$, 则$Q^v(\mathbf{v})$的系数矩阵约等于$k \mathbf{A} \approx k \mathbf{n} \mathbf{n}^T$, 为一个秩1矩阵. 从而$Q^v(\mathbf{v})$的系数矩阵的最小奇异值约为0, 条件数趋近于无穷大, 为一个病态矩阵.
$\\$ 请注意, 属性不会贡献任何零奇异值, 因为$\mathbf{A}$的对角线上大小为$m \times m$的$k$个子矩阵均为单位矩阵$\mathbf{I}$. 当线性方程组的系数矩阵为病态矩阵时, 本文令$\mathbf{p} = \mathbf{p}_1 + $$ \mathbf{p}_2$, 而后再次求解$\{ s_1, \dots, s_k \}$.