最近每天的天气都是火炉天气, 在家里实在是有点难受, 个人感觉去年同一时候的温度要低一些…… 本文主要是关于纤维化与复迭映射一节内容的注记, 除了书上的内容之外, 自己还会学习庄晓波老师关于覆盖映射的相关视频, 以此加深对这一节内容的理解.
参考材料
1. Lebesgue number lemma
2. solutions_09
3. 为什么说离散空间中,X的每一个子集都是开集?
4. The fiber of a covering space over a connected space has constant cardinality [duplicate]
5. 4-sheet covering of the wedge sum of two circles
6. How do I see that the fundamental group of M is finite?
1. 书上P233定理5.2.1的证明中使用了Lebesgue引理, 其引理内容详见参考材料1. 由于$[0, 1]$是一个序列紧的度量空间, 故Lebsgue引理的使用是合理的. 类似地, 由于证明中构造的均匀复迭邻域的原像是开集, 且$[\frac{i}{n}, \frac{i + 1}{n}]$是紧致的, 故管状引理的使用亦是合理的.
$\\$ 此外, 书上并未对连续扩张的唯一性进行详细论述, 后续需要补充此处细节.
2. 把圆周绕自己$n$圈的映射$$f_\pi : S^1 \to S^1, (cos(2\pi t), sin(2\pi t)) \mapsto (cos(2n\pi t), sin(2n\pi t))$$是一个$n$层复迭.
$\\$ 证: 我们从复数的角度出发, 将问题转化为如下形式:$$p: S^1 \to S^1, p(z) := z^n$$是一个$n$层复迭.
$\\$ 首先要注意1的$n$次方根, 即$z^n = 1$的解为$$\xi_k := e^{2\pi ik/n} = cos(2\pi k / n) + i sin(2\pi k / n), k = 1, \cdots, n.$$因此, 给定任意$z = e^{i\theta} \in S^1$, 我们有$$p^{-1}(z) = \{ e^{i\theta / n} \xi_1, e^{i\theta / n} \xi_2, \cdots, e^{i\theta / n} \xi_n \}.$$取定$z_0 = e^{i\theta_0} \in S^1$, 令$U := \{ e^{i\theta} : |\theta – \theta_0 | < \pi / 2\} \subseteq S^1$为$z_0$的一个均匀复迭邻域. 根据参考材料1中的命题9.1, 可得$p^{-1}(U) = \cup_{k = 1}^n V_k$, 其中$$V_k := \{ e^{i\theta /n} \xi_k : |\theta - \theta_0| < \pi / 2 \}.$$注意到$V_k \cap V_h = \emptyset, \forall k \ne h$. 事实上, 假设$\exists \theta, \theta' \in (\theta_0 - \pi /2, $$ \theta_0 + \pi / 2)$, $e^{i\theta / n} \xi_k = e^{i\theta' / n} \xi_h, k \ne h$, 则$$\frac{\theta}{n} + \frac{2\pi k}{n} \equiv \frac{\theta'}{n} + \frac{2\pi h}{n} (mod \ 2\pi) \\ \Longleftrightarrow \theta - \theta' \equiv 2\pi (h - k) (mod \ 2\pi n).$$但$|\theta - \theta'| < \pi < 2\pi |h - k| < 2\pi n$, 这与上述等式相矛盾. 故$\{ $$ V_k \}_{k = 1, \cdots, n}$两两无交. 更进一步地, 对于$k = 1, \cdots, n$, $p | V_k : V_k $$ \to U$是一个连续双射. 此外, 对于任意$e^{i\theta} \in U$, 即$|\theta - \theta_0| < \pi / 2$, $p | V_k$的逆映射$(p | V_k)^{-1} : U \to V_k$可定义如下$$(p | V_k)^{-1}(e^{i\theta}) = e^{i\theta / n} \xi_k.$$故$(p | V_k)^{-1}$亦是连续的, 从而证明了对于$\forall k = 1, \cdots, n$, $p | V_k : $$ V_k $$ \to U$是一个同胚. 命题得证.
$\\$ $\\$ 3. 设$f: E \to B \times F$是同胚, $p: B \times F \to B, (x, y) \mapsto x$是投射. 证明$p \circ $$ f: E \to B$是一个纤维化.
$\\$ 证: 这个命题的证明其实不难, 但自己一开始不理解该命题的证明的原因是搞混了纤维化与复迭映射的概念.
$\\$ $\\$ 4. 设$p: E \to B$是复迭映射, 任取$x \in B$, 证明纤维$p^{-1}(x) \subseteq E$是离散拓扑空间(即每个单点集是开集).
$\\$ 证: 对于任意$x \in B$, 我们首先证明: $p^{-1}(x)$为一个离散子集, 即对于任意$y \in E$, 存在一个$y$的开邻域$U$使得$(U \backslash \{ y \}) \cap p^{-1}(x) = \emptyset$. 我们需要对下述两种情况分别进行讨论:
$\\$ $\cdot$ 若$y \in p^{-1}(x)$, 取$x$的一个均匀复迭邻域$V$, 则$p^{-1}(V) = \cup_{i \in I}U_i$, 其中$U_i \subseteq $$ E$是两两无交的, 且均同胚于$V$. 特别地, $U_i$均为开集, 且对于$\forall i \in I$, 存在唯一的$y_i \in p^{-1}(x) \cap U_i$. 因此我们可以令$U := $$ U_i$, 其中$y \in U_i$, 这亦是$y$的一个开邻域, 使得$(U \backslash \{ y \}) \cap p^{-1}(x) $$ = \emptyset$.
$\\$ $\cdot$ 若$p(y) \ne x$, 由于$B$是Hausdorff的(事实上, $B$仅需满足T1公理即可, 这是额外假设???), 故我们可取$p(y)$的一个不包含$x$的均匀复迭邻域$V$, 其原像$U := $$ p^{-1}(V)$是$y$的一个不包含$p^{-1}(x)$的任意元素的开邻域(因为$U$同胚于$V$且$x \notin $$ V$), 从而我们可得$(U \backslash \{ y \}) \cap $$ p^{-1}(x) = \emptyset$.
$\\$ 接下来我们来证明$p^{-1}(x)$为一个有限子集, 不妨假设$E$是紧致的, 则一个紧致拓扑空间的任意离散子集均是离散的; 否则, 我们假设在紧致拓扑空间$E$中存在一个无限离散子集$A$. 由离散子集的定义, 对于任意$y \in E$, 存在$y$的一个开邻域$U_y$, 使得$(U_y \backslash \{ y \}) \cap A = \emptyset$. 根据$E$的紧致性, $E$的开覆盖$\{ U_y \}_{y \in E}$有一个有限子覆盖$\{ U_{y_1}, \cdots, $$ U_{y_n} \}$, 则我们有$$\emptyset = ((U_{y_1} \backslash \{ y_1 \}) \cup \cdots \cup (U_{y_n} \backslash \{ y_n \})) \cap A \\ \supseteq ((U_{y_1} \cup \cdots \cup U_{y_n}) \backslash \{ y_1, \cdots, y_n \}) \cap A,$$从而$A \subseteq \{ y_1, \cdots, y_n \}$是有限的.
$\\$ 最后我们证明在离散子集$p^{-1}(x)$可定义离散拓扑. 我们不妨在离散子集$p^{-1}(x)$上定义离散距离$d_d$:$$d_d(x, y) = \left\{\begin{matrix}
1 & if \ x \ne y, \\
0 & if \ x = y.
\end{matrix}\right.$$这个距离下$\{ x \} = Ball(x, 1)$, 也就是说每个圆心$x$的”单位开球” 就是这个圆心本身. 因为在距离空间中度量诱导出来的开集定义为: $U$为一个开集, 当且仅当对于任意$x \in U$, 存在一个开球$Ball(x, d) $$ := \{ x; d(x, d) \} \subset U$. 事实上, 由参考材料3中提及的定理, 离散距离诱导出来的拓扑和离散拓扑等价, 即每个点都是开集(因为是一个开球), 由于每个集合都是其中的单点的开集, 自然每个集合都是开集. 也就是说$$A = \cup_{x \in A} Ball(x, 1) = \cup_{x \in A} \{ x \}.$$若我们直接对一个空间赋予离散拓扑$X = R, \tau = 2^R$, 也就是说任何子集都是在这个拓扑$\tau = 2^R$下的开集, 则这个拓扑和用距离空间诱导出的拓扑是等价的. 综上所述, 命题得证.
5. 设$p: E \to B$是复迭映射, 如果$B$道路连通, 则任取$x, y \in B$, $p^{-1}(x) \cong $$ p^{-1}(y)$.
$\\$ 证: 不妨将条件弱化, 证明更一般的结论: 设$p: E \to B$是复迭映射, 如果$B$连通, 则任取$x, y \in B$, $p^{-1}(x) \cong $$ p^{-1}(y)$. 由上述结论, 即须证明: 若对于一些$b_0 \in $$ B$, $p^{-1}(b_0)$含有$k$个元素, 则对于任意$b \in B$, $p^{-1}(b)$含有$k$个元素.
$\\$ 假设存在$b_0 \in B$, $p^{-1}(b_0)$含有$k$个元素. 令$A := \{ b \in B: |p^{-1}(b $$ )| = k \}$, 注意到
$\\$ 1) $\because b_0 \in A$, $A \ne \emptyset$.
$\\$ 2) $A \cap (B \backslash A) = \emptyset$.
$\\$ 3) $A \cup (B \backslash A) = B$.
$\\$ 4) $A$为开集.
$\\$ 5) $B \backslash A$为开集.
$\\$ 若以上五点均成立, 则可推出$B \backslash A = \emptyset$, 否则我们可以得到$B$的一个分割, 这与$B$的连通性矛盾. 故$B \backslash A = \emptyset \Rightarrow A = B$, 从而任意$p$的纤维(即$p^{-1}(b)$) 含有$k$个元素.
$\\$ 前面三点是显然的, 接下来我们证明后面两点. 首先证明4): 令$a \in A$, 因为$p$为一个复迭映射, 故存在开集$U \ni a$使得$p^{-1}(U) = $$ \cup_{\alpha \in \Lambda} V_\alpha$, 其中每个$V_\alpha$均通过$p | V_\alpha$同胚于$U$. 由于$p^{-1}(a)$与每个$V_\alpha$仅相交于一点, 故$\Lambda$含有$k$个元素, 我们可将$p^{-1}(U)$写为$p^{-1}(U) = \cup_{n = 1}^k V_n$. 任取$x \in U$, 则$p^{-1}(x) \subseteq p^{-1}(U) = $$ \cup_{n = 1}^k V_n$. 又$p | V_n$是一个同胚, 则$p^{-1}(x)$亦含有$k$个元素, 从而$x \in A$. 因为$\forall a \in $$ A$, $a \in U \subseteq A$, 故$A$是一个开集. 同理可证明5).
综上所述, 命题得证.
6. 请画图描述出两个圆周的一点并$S^1 \vee S^1$的两种全空间相互不同胚的4层复迭.
$\\$ 解: 由上述结论, 由于两个圆周的一点并$S^1 \vee S^1$是道路连通的, 故$p^{-1}(x)$含有的元素数量是复迭映射$p: E \to S^1 \vee S^1$的Number of Sheets.
$\\$ Hatcher的Algebraic Topology的P58上的例7, 8, 9均给出了两个圆周的一点并$S^1 \vee S^1$的4层复迭. 以例7为例, 如下图所示.
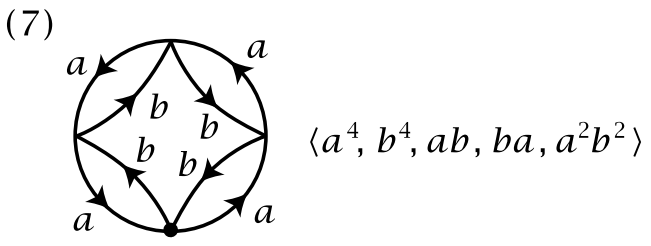
在圆的内部包含一个变形的正方形, 这个变形的正方形与圆相交于4个点. 这4个点是两个圆周的一点并$S^1 \vee S^1$的基点在复迭映射下的原像, 该复迭映射同时也将$E$中的边$b$映射至两个圆周的一点并$S^1 \vee $$ S^1$中的对应边(此处亦记为$b$), 边$a$亦然. 故复迭映射$p: E \to S^1 \vee $$ S^1$的Number of Sheets等于变形的正方形与圆的相交的顶点数, 4.
7. 设$p: E \to B$是有限复迭, $q: \widetilde{E} \to E$也是复迭映射, 证明$p \circ q $$ : $$ \widetilde{E} \to B$是复迭映射.
$\\$ 证: 取$b \in B$, 令$y_1, \cdots, y_n$为$b$在映射$p$下的原像, $U$为$b$在复迭映射$p: $$ E \to B$下的均匀复迭邻域. 对于$\forall i = 1, \cdots, n$, 令$U_i$为$y_i$在复迭映射$q: \widetilde{E} \to E$下的均匀复迭邻域, $V := U_i \cap q^{-1}(U)$, 则我们有
$\\$ $\cdot$ $V_i$为$y_i$的均匀复迭邻域(某点的均匀复迭邻域的包含该点的开子集仍为该点的均匀复迭邻域);
$\\$ $\cdot$ $p | _{V_i}$为$V_i$与$p(V_i)$之间的同胚;
$\\$ $\cdot$ $V_i$其为复迭映射$q: \widetilde{E} \to E$下的均匀复迭邻域.
$\\$ 接下来, 我们定义$W \subseteq B$为$$W := \bigcap_{i = 1}^{n} p(V_i).$$由于$n$是有限的, $W$为$B$的一个开子集. 此外, 由于$W$被包含在$b$的一个在复迭映射$p: E \to B$下的均匀复迭邻域中, 故$W$亦为$b$的一个均匀复迭邻域. 另一方面, 由于$p^{-1}(W) \subseteq \cup^n_{i = 1}V_i$, 我们有$p^{-1}(W) $$ = $$ \cup^n_{i = 1}W_i$, 其中, 对于$\forall i = 1, \cdots, $$ n$, $W_i$被包含于$V_i$中, 故$W_i$亦为$y_i$的在复迭映射$q: \widetilde{E} \to E$下的两两不相交的均匀复迭邻域.
$\\$ 最后我们来证明$W$是$b$的一个在复迭映射$p \circ q$下的均匀复迭邻域. 注意到$(p \circ $$ q)^{-1}(W) = \cup^n_{i = 1}q^{-1}(W_i)$, 其中$q^{-1}(W_i)$是两两不相交的(因为$W_i$是两两不相交的). 此外, 由于任一$W_i$均为复迭映射$q$下的均匀复迭邻域, 我们有$q^{-1}(W_i) $$ = \cup_{j \in J_i}T_i^j$, 其中, $T_j^i \subseteq \widetilde{E}$是两两不相交的, $q | _{T_i^j} : T_i^j \to W_i$为一个同胚. 因此, 我们可得$(p \circ q $$ ) | _{T_i^j} = p | _{W_i} $$ \circ q | _{T_i^j} : T_i^j \to W$为一个同胚, 因为它为两个同胚的复合. 综上所述, $W$为$b \in B$的一个在复迭映射$p \circ q$下的均匀复迭邻域. 根据$b $$ \in B$的选取的任意性, 命题得证.
8. 设$X$是一个以$S^n$为复迭空间的$n$维流形, 证明这个复迭一定是有限复迭.
$\\$ 证: 取定$x \in X$, $p^{-1}(x)$是$S^n$的闭子集, 因此紧致. 于是取$x$的一个均匀复迭邻域$U$, 则$p^{-1}(U) = \cup_{i = 1}^m U_i$的有限多层就可以覆盖$p^{-1}( $$ x)$了. 若$m$是无限的, 则由于$U_i$是两两不相交的, $p^{-1}(U) = $$ \cup_{i = 1}^m U_i$除去一个有限子覆盖以后, 不包含$p^{-1}(x)$中的任何点, 这与复迭映射的定义矛盾. 综上所述, $m$是有限的, 命题得证.
$\\$ PS: 该命题亦可从同调群的角度出发去证明, 详见参考材料6.